Косинус - это одна из основных тригонометрических функций, которая широко применяется в математике и физике. Интересная особенность косинуса заключается в его четности. На первый взгляд может показаться, что косинус имеет случайную четность, но на самом деле существует простое правило, которое объясняет эту особенность.
Четность математической функции - это свойство, указывающее на симметрию функции относительно оси ординат. Если функция является четной, то она сохраняет свой знак при зеркальном отражении относительно оси ординат. Если функция является нечетной, то она меняет свой знак при таком отражении.
Косинус является четной функцией. Это означает, что если аргумент функции умножить на -1, то результат будет равен исходному значению. Математически это записывается следующим образом: cos(-x) = cos(x). Таким образом, основное свойство четности косинуса объясняет, что косинус симметричен относительно оси ординат.
Пример:Условие: Дано значение косинуса 0.8. Найти значение аргумента косинуса.
Решение: Используя свойство четности косинуса, мы можем записать уравнение вида cos(x) = 0.8. Поскольку косинус является четной функцией, это уравнение будет иметь два решения: x = arccos(0.8) и x = -arccos(0.8). Таким образом, значения аргумента косинуса будут равны примерно 0.643 и примерно -0.643.
Четность косинуса: основные идеи и свойства

Четность функции означает, что ее значение не зависит от знака аргумента. Другими словами, функция является симметричной относительно оси ординат. В контексте косинуса, его четность означает следующее: если для некоторого угла α значение косинуса равно x, то для угла -α значение косинуса также будет равно x.
Математические свойства косинуса:
- Косинус является четной функцией: cos(-α) = cos(α).
- Значение косинуса находится в пределах от -1 до 1, включительно: -1 ≤ cos(α) ≤ 1.
- Косинус периодичен с периодом 2π: cos(α + 2π) = cos(α).
- Косинус имеет максимум при α = 0 и минимумы при α = π/2 и α = -π/2.
Примеры использования:
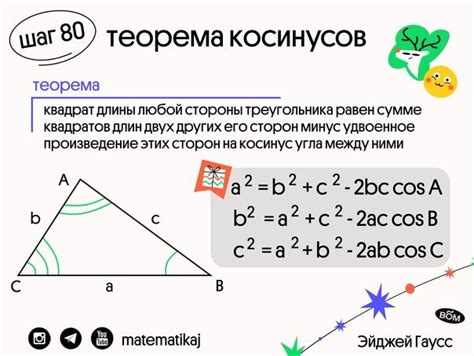
Представим, что у нас есть прямоугольный треугольник с гипотенузой равной 5 и прилежащим катетом равным 4. Мы хотим найти значение косинуса угла α, где α – угол между гипотенузой и прилежащим катетом. Применяя треугольниковый косинус, мы получаем: cos(α) = 4/5 = 0.8. Теперь мы можем использовать это значение, чтобы найти косинус другого угла, например, -α, и убедиться, что получим такое же значение косинуса 0.8.
В заключение, четность косинуса является важным свойством, которое позволяет использовать значения косинуса для различных углов, в том числе и их отрицательных аналогов, без необходимости повторного вычисления.
Косинус: определение и специфика
Основные характеристики косинуса:
- Значение косинуса всегда находится в диапазоне от -1 до 1.
- Косинус является четной функцией, то есть cos(-x) = cos(x).
- Максимальное значение косинуса равно 1 и достигается при угле 0° (или 360°).
- Минимальное значение косинуса равно -1 и достигается при угле 180°.
- Косинус является периодической функцией с периодом 360° (или 2π радиан).
Косинус широко используется в различных областях науки и техники. Он применяется в физике для вычисления сил, связанных с углами, в математике для решения треугольных и геометрических задач, а также в сфере информационных технологий для обработки сигналов и изображений.
Четность функций: краткое объяснение
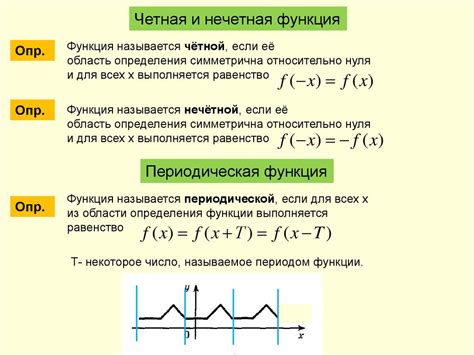
Функция называется четной, если для любого значения аргумента $x$ выполняется условие: $f(x) = f(-x)$. Это означает, что график четной функции симметричен относительно оси $y$.
Примером четной функции является функция $f(x) = x^2$. Для любого значения $x$ выполнено равенство $f(x) = f(-x)$, что демонстрирует симметричность графика функции относительно оси $y$.
Функция называется нечетной, если для любого значения аргумента $x$ выполняется условие: $f(x) = -f(-x)$. Это означает, что график нечетной функции также симметричен относительно начала координат.
Примером нечетной функции является функция $f(x) = x^3$. Для любого значения $x$ выполнено равенство $f(x) = -f(-x)$, что демонстрирует симметричность графика функции относительно начала координат.
Таким образом, понимание свойств четности функций позволяет более глубоко исследовать и анализировать различные математические функции и их графики.
Свойства и обоснование четности косинуса
Геометрическое объяснение четности косинуса основано на его определении в прямоугольной треугольнике. Рассмотрим прямоугольный треугольник ABC, где угол BAC равен α. Пусть точка M - середина гипотенузы, а точка N лежит на гипотенузе так, что угол ANB равен α.
Из геометрических соображений следует, что косинус угла α равен отношению катета AC к гипотенузе AB. Таким образом, cos(α) = AC / AB.
Теперь рассмотрим угол -α. По определению, косинус угла -α равен отношению катета A′C к гипотенузе AB. Очевидно, что катет A′C равен катету AC, поскольку это одна и та же сторона треугольника ABC. Таким образом, cos(-α) = AC / AB, что идентично cos(α).
Алгебраическое объяснение четности косинуса основано на его определении с использованием экспоненциальной формулы. Косинус угла α можно представить в виде:
- cos(α) = (e^(iα) + e^(-iα)) / 2,
- cos(-α) = (e^(-iα) + e^(iα)) / 2.
Но так как e^(-iα) = 1 / e^(iα), то получается:
cos(-α) = (1 / e^(iα) + e^(iα)) / 2 = (e^(iα) + e^(-iα)) / 2, что равно cos(α).
Таким образом, получаем, что косинус угла α и косинус угла -α равны друг другу, что и означает четность косинуса.
Особенности косинуса: единица и ноль
Существует два особых значения косинуса: единица и ноль.
Единица (cos 0° = 1)
Косинус угла 0 градусов равен 1. Это означает, что когда угол между векторами или сторонами равен 0 градусов, их направления совпадают полностью. Таким образом, при угле 0 градусов косинус равен 1, что символизирует совпадение направлений и полную совпадение векторов.
Ноль (cos 90° = 0)
Косинус угла 90 градусов равен 0. Это означает, что когда угол между векторами или сторонами равен 90 градусов, они оказываются перпендикулярными друг другу. Таким образом, при угле 90 градусов косинус равен 0, что символизирует отсутствие совпадения направлений и полное перпендикулярное положение векторов.
Эти основные значения косинуса (1 и 0) имеют важное значение в различных областях знаний, таких как физика, математика, инженерия и компьютерные науки.
График косинуса: отражение и периодичность
Периодичность графика функции косинуса означает, что он повторяется через определенные интервалы. Период функции косинуса равен 2π радиан или 360 градусов. То есть, косинус имеет одинаковое значение на каждом интервале длиной 2π или 360 градусов.
Отражение графика косинуса относительно оси OX может быть проиллюстрировано путем замены x на -x. Как результат, значения косинуса при отрицательных значениях x будут равны значениям косинуса при положительных значениях x, только с противоположным знаком.
График косинуса имеет форму колебательной волны, амплитуда которой варьируется от -1 до 1. Максимальная амплитуда достигается в точках, где значение косинуса равно 1 или -1, а минимальная амплитуда - в точках, где значение косинуса равно 0.
Изучение графика косинуса и его свойств позволяют нам лучше понять его поведение и использовать его в различных областях, таких как физика, математика, инженерия и другие.
Нечетность косинуса: альтернативная характеристика

Если для любого значения аргумента x выполняется равенство cos(-x) = -cos(x), то функция cos(x) является нечетной.
То есть, если мы возьмем отрицательное значение аргумента и посчитаем косинус от этого отрицательного значения, а затем найдем противоположное число от полученного значения, результат должен совпасть с косинусом от положительного значения аргумента.
Аналогично, можно сказать, что функция синус является нечетной, так как sin(-x) = -sin(x) для любого значения аргумента x.
Нечетность косинуса может быть использована в различных алгебраических преобразованиях и решении уравнений. Она позволяет сделать определенные выводы о поведении функции в отношении ее симметрии.








