Парабола - одна из самых известных кривых в математике. Она имеет множество применений в науке и технике. Одно из ключевых понятий, связанных с параболой, - это ось симметрии. Ось симметрии параболы является важным элементом, описывающим ее форму и свойства.
Ось симметрии параболы - это вертикальная прямая, которая делит параболу на две симметричные части. Вся парабола симметрична относительно этой оси и имеет одинаковую форму и расстояние до оси симметрии в любой точке.
Ось симметрии параболы можно найти с помощью ее уравнения. Общее уравнение параболы имеет вид y = ax^2 + bx + c, где a, b и c - постоянные значения. Ось симметрии параболы всегда проходит через вершину, которая находится в точке с координатами (-b/2a, c - b^2/4a).
Таким образом, уравнение параболы содержит важную информацию о ее оси симметрии и вершине. Зная эти параметры, можно определить расположение параболы на координатной плоскости и ее форму.
Понимание оси симметрии параболы и уравнения, описывающего ее, имеет большое значение в различных областях, таких как физика, инженерия, компьютерная графика и другие. Зная ось симметрии, можно моделировать параболические конструкции и предсказывать их поведение.
Таким образом, ось симметрии параболы является важным понятием, позволяющим понять и описать ее форму и свойства. Уравнение параболы содержит информацию о ее оси симметрии и вершине, что позволяет использовать ее в различных сферах деятельности.
Симметрия параболы: общее представление
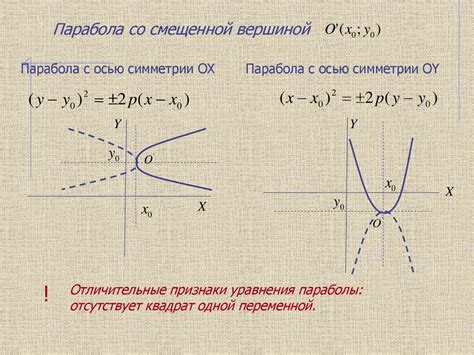
При изучении параболы ось симметрии играет особую роль. Ось симметрии параболы проходит через ее вершину (точку, в которой график параболы имеет экстремальное значение). Это означает, что если мы возьмем точку на одной стороне параболы относительно его оси симметрии и отразим ее относительно этой оси, то получим точку, которая будет отражать другую точку на другой стороне параболы.
Уравнение параболы используется для определения ее осей симметрии. Уравнение параболы в общем виде имеет вид y = ax^2 + bx + c, где a, b и c – коэффициенты, определяющие форму и положение параболы. При аргументе x, равном нулю, значение уравнения равно c. Если ось симметрии параболы проходит через вершину параболы, то значения c и -c будут равны, так как вершина параболы будет располагаться на оси симметрии.
Пример: рассмотрим уравнение параболы y = x^2. Она имеет вершину в точке (0,0) и ось симметрии, проходящую через эту вершину. Если мы возьмем точку на одной стороне параболы, например (2,4), и отразим ее относительно оси симметрии, то получим точку (-2,4), которая будет отражать первоначальную точку на другой стороне параболы.
Важность осей симметрии для геометрического анализа параболы
Оси симметрии позволяют нам легко определить ряд важных характеристик параболы, таких как ее уравнение, фокусное расстояние и точку вершины. Зная оси симметрии, мы можем с легкостью определить уравнение параболы и использовать его для проведения дальнейшего анализа. Например, длина оси симметрии позволяет нам определить фокусное расстояние и точку вершины параболы.
Оси симметрии также помогают нам в визуальном анализе параболы. Зная положение осей симметрии, мы можем более точно представить себе форму и симметрию параболы. Это полезно при решении различных задач, связанных с параболическими кривыми.
В заключение, оси симметрии являются важным элементом геометрического анализа параболы. Они позволяют нам определить ключевые характеристики параболы, такие как уравнение, фокусное расстояние и точку вершины, а также помогают нам в визуальном анализе и понимании ее формы и симметрии.
Уравнение параболы как ключевой фактор определения осей симметрии
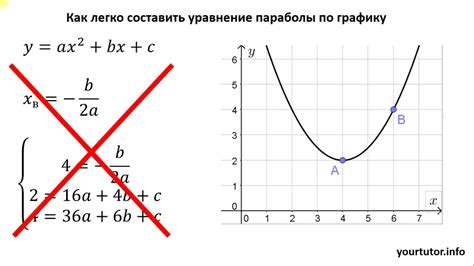
Оси симметрии параболы являются двумя важными линиями, которые делят параболу на две равные части. Они симметричны относительно оси y и играют значительную роль в определении свойств параболы.
Уравнение параболы имеет вид y = ax^2 + bx + c, где a, b и c - коэффициенты, определяющие форму и положение параболы. При анализе осей симметрии параболы, значение коэффициента b становится критически важным.
Если коэффициент b равен нулю (b = 0), то ось симметрии проходит через вершину параболы. Получается, что парабола симметрична относительно оси y.
Если коэффициент b не равен нулю (b ≠ 0), то ось симметрии параболы можно найти по формуле x = -b / (2a). Она проходит через вершину параболы и является перпендикулярной оси y.
Таким образом, уравнение параболы является ключевым фактором в определении осей симметрии. Зная значения коэффициентов a и b, можно определить положение и форму параболы, а также найти ее оси симметрии. Это позволяет проводить более глубокий анализ и изучение параболы в математике и других науках.
Практическое применение знания об оси симметрии и уравнении параболы
Знание оси симметрии и уравнения параболы имеет практическое применение в различных областях, включая математику, физику, инженерию и компьютерную графику.
В математике и физике ось симметрии используется для упрощения задач и нахождения симметричных решений. Например, при решении задач на построение графиков или нахождение экстремумов функций ось симметрии может помочь определить общую форму графика и сократить необходимые вычисления.
Оси симметрии параболы также широко используются в инженерии при проектировании линз, отражателей и антенн. Знание оси симметрии и уравнения параболы позволяет инженерам оптимизировать форму и размеры этих объектов для достижения оптимальных характеристик.
В компьютерной графике ось симметрии и уравнение параболы используются для создания реалистичных и эффективных 3D-моделей объектов. Параболические кривые могут быть использованы для моделирования различных объектов, таких как дуги мостов, спутниковые тарелки и спецэффекты в видеоиграх.
Знание оси симметрии и уравнения параболы позволяет решать различные задачи и создавать эффективные решения в различных областях, от науки и техники до искусства и развлечений.








