Упрощение многочлена – это процесс, при котором выражение, состоящее из нескольких слагаемых, приводится к более простому виду. Упрощение многочлена может быть полезным в решении математических задач, таких как определение корней уравнений или нахождение значений для заданных переменных.
Для упрощения многочлена, необходимо выполнить некоторые операции, такие как суммирование и вычитание слагаемых, сокращение подобных членов и применение различных математических свойств и формул.
Приведем пример упрощения многочлена:Рассмотрим многочлен: 3x2 + 2x + 5x - 7
Для начала, мы можем объединить похожие слагаемые: 3x2 + (2x + 5x) - 7
Теперь, объединяем подобные члены в скобках: 3x2 + 7x - 7
Таким образом, мы упростили многочлен до более простого вида.
Упрощение многочлена является важной концепцией в алгебре и математике в целом. Это позволяет нам лучше понять и анализировать сложные выражения и сокращать их до более удобных и понятных форм.
Что такое упрощение многочлена?
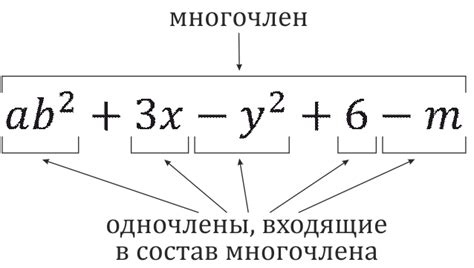
Многочлен – это математическое выражение, состоящее из переменных, коэффициентов и операций сложения и умножения. Он может содержать одну или несколько переменных, например:
y = 2x^2 + 3x + 1
Упрощение многочлена включает в себя следующие шаги:
- Упорядочение членов – члены многочлена упорядочиваются по убыванию степеней переменных. Например:
y = 2x^2 + 3x + 1
Здесь член 2x^2 имеет наивысшую степень переменной x, член 3x имеет степень переменной x на единицу меньше, а число 1 – это свободный член.
- Сокращение подобных членов – подобные члены имеют одинаковые степени переменных. Их коэффициенты складываются или вычитаются вместе, а переменные остаются без изменений. Например:
y = 2x^2 + 3x + 1
Так как здесь нет реальных подобных членов, то процесс сокращения подобных членов не выполняется.
Упрощенный многочлен будет выглядеть так:
y = 2x^2 + 3x + 1
Упрощение многочлена позволяет сделать его более компактным и понятным для анализа и работы с ним.
Понятие упрощения многочлена
Многочлен может содержать разные переменные, степени переменных и коэффициенты. В процессе упрощения многочлена, мы стремимся упростить его до такой формы, в которой каждый моном будет иметь наибольшую возможную степень переменной и привести подобные слагаемые к единой форме.
Упрощение многочлена включает в себя следующие шаги:
- Сортировка слагаемых по убыванию степеней переменных.
- Сбор подобных слагаемых.
Перейдем к примеру, чтобы лучше понять процесс упрощения многочлена.
Рассмотрим многочлен: 3x^3 + 2xy - 5x^2 + 7y - 4xy - x^3.
Шаг 1: Сортировка слагаемых по убыванию степеней переменных:
- -x^3 + 3x^3 - 5x^2 + 2xy - 4xy + 7y
Шаг 2: Сбор подобных слагаемых:
- (-x^3 + 3x^3) - 5x^2 + (2xy - 4xy) + 7y
- 2x^3 - 5x^2 - 2xy + 7y
Таким образом, многочлен 3x^3 + 2xy - 5x^2 + 7y - 4xy - x^3 после упрощения принимает вид 2x^3 - 5x^2 - 2xy + 7y.
Для чего нужно упрощать многочлены

Упрощение многочленов с помощью различных математических операций, таких как объединение подобных слагаемых, факторизация и удаление лишних членов, позволяет сократить количество членов в многочлене и упростить его уравнение. Это особенно полезно при решении задач, где требуется найти корни многочлена или привести его к канонической форме.
Упрощение многочленов имеет несколько целей:
- Сокращение сложности выражения для упрощения его анализа и решения;
- Выявление ключевых характеристик многочлена, таких как степень, коэффициенты, корни;
- Построение графиков для визуализации функции, описываемой многочленом;
- Упрощение вычислений и упрощение алгебраических манипуляций.
Упрощение многочленов дает возможность увидеть и использовать основные свойства и закономерности, связанные с многочленами, такие как связь между коэффициентами и корнями, разложение многочлена на множители и т.д.
В результате, упрощенный многочлен становится более компактным и понятным, что облегчает его анализ и решение. Он также может быть использован для установления зависимостей и создания моделей в различных областях науки, техники и экономики.
Как упростить многочлен
Для упрощения многочлена необходимо выполнить следующие шаги:
- Объединить подобные члены. Подобные члены это члены, у которых одинаковые степени переменных. Например, в многочлене 3x^2 + 2x^2 + 5x, два члена 3x^2 и 2x^2 являются подобными, поэтому их можно объединить в один член 5x^2. Аналогично, можно объединить все подобные члены.
- Сложить коэффициенты подобных членов. После объединения подобных членов, следует просуммировать коэффициенты. В примере выше, сумма коэффициентов 3 и 2 равна 5.
- Удалить нулевые члены. Если после объединения подобных членов получился нулевой член, его можно полностью убрать из многочлена. Например, в многочлене 5x^2 + 3x - 5x^2 - 3x, два подобных члена 5x^2 и -5x^2 объединяются и дают 0x^2, что можно просто записать как 0.
Пример упрощения многочлена:
Исходный многочлен: 2x^2 + 3x - 4x^2 + 5
Объединение подобных членов: (2x^2 - 4x^2) + 3x + 5 = -2x^2 + 3x + 5
Сложение коэффициентов: (-2 + 3)x^2 + 5 = x^2 + 5
Таким образом, исходный многочлен 2x^2 + 3x - 4x^2 + 5 упрощается до x^2 + 5.
Основные принципы упрощения многочлена

Основные принципы упрощения многочлена:
- Сокращение подобных членов. Подобные члены - это члены с одинаковыми степенями переменных. Для упрощения многочлена необходимо объединить подобные члены путем сложения или вычитания их коэффициентов.
- Удаление нулевых коэффициентов. Если коэффициент перед членом равен нулю, то его можно полностью исключить из многочлена, так как он не влияет на значение многочлена.
- Использование свойств алгебры. Для упрощения многочлена можно использовать свойства алгебры, такие как коммутативность, ассоциативность и дистрибутивность операций сложения и умножения.
- Факторизация. Если возможно, многочлен можно упростить, разложив его на простые множители с помощью факторизации.
Пример упрощения многочлена:
Дан многочлен 2x^3 + 4x^2 - 3x^3 - 10x^2 - 5x + 2.
Применяя принципы упрощения, мы можем сначала объединить подобные члены:
2x^3 - 3x^3 + 4x^2 - 10x^2 - 5x + 2 = (-x^3) - 6x^2 - 5x + 2.
Затем мы можем удалить нулевые коэффициенты:
(-x^3) - 6x^2 - 5x + 2.
Таким образом, мы упростили многочлен и представили его в более простой форме.
Примеры упрощения многочленов
Рассмотрим несколько примеров упрощения многочленов:
1. Пример:
Дано многочлен: 3x3 + 2x2 - 5x + 4
Упростим выражение:
3x3 + 2x2 - 5x + 4
В данном случае многочлен уже находится в упрощенной форме, так как все его слагаемые являются членами одинаковой степени.
2. Пример:
Дано многочлен: 4x2 - 7x - 2x3 + 5
Упростим выражение, переставив слагаемые так, чтобы члены с одинаковыми степенями шли друг за другом:
-2x3 + 4x2 - 7x + 5
Таким образом, многочлен был упрощен.
3. Пример:
Дано многочлен: 2x4 - 3x2 + 6x3 - 5x - 1
Упростим выражение, перегруппировав члены по убыванию степеней:
2x4 + 6x3 - 3x2 - 5x - 1
Таким образом, многочлен был упрощен.
Упрощение многочлена позволяет сделать его вид более понятным и удобным для дальнейших математических операций, таких как сложение, вычитание, умножение и деление многочленов.
Упрощение многочленов с помощью арифметических операций

Для упрощения многочлена мы используем различные арифметические операции, такие как сложение, вычитание, умножение и деление. Главная цель упрощения многочлена – упростить его структуру и сократить количество членов.
Основные шаги упрощения многочлена:
1. Сложение и вычитание членов
Мы можем сложить или вычесть различные члены многочлена, объединяя их похожие составляющие. Например:
2x + 3x = (2 + 3)x = 5x
В этом примере мы сложили два одинаковых члена многочлена.
2. Умножение и деление членов
Мы также можем упрощать многочлены, умножая или делая члены многочлена на константы. Например:
2x * 3 = 6x
В этом примере мы умножили член многочлена на константу 3.
3. Сокращение подобных членов
Подобные члены – это члены многочлена, которые имеют одинаковую степень и одинаковые переменные. Мы можем сократить подобные члены, складывая или вычитая их коэффициенты. Например:
2x + 3x + 4x = (2 + 3 + 4)x = 9x
В этом примере мы сложили три подобных члена многочлена и упростили его до одного члена.
При упрощении многочлена очень важно следить за знаками и правильно применять арифметические операции. Если многочлен содержит скобки, их нужно раскрыть перед тем, как выполнять операции со смежными членами.
Упрощение многочленов с помощью факторизации
Факторизация многочлена заключается в разложении его на простейшие множители. Простейшим множителем многочлена является такой множитель, который уже не может быть разложен на более простые множители. Например, для многочлена x^2 - 4, простейшими множителями являются (x - 2) и (x + 2).
Процесс упрощения многочлена с помощью факторизации состоит из следующих шагов:
- Нахождение простейшего множителя многочлена. Для этого используются различные методы, такие как метод группировки или применение формул суммы и разности квадратов.
- Факторизация многочлена путем выноса найденного множителя за скобку и раскрытие скобок.
- Повторение шагов 1 и 2 для оставшихся множителей до тех пор, пока все множители не станут простыми.
Пример упрощения многочлена с помощью факторизации:
| Исходный многочлен | Факторизация | Упрощенный многочлен |
|---|---|---|
| x^2 + 3x + 2 | (x + 1)(x + 2) | (x + 1)(x + 2) |
В данном примере, применяя метод группировки, мы находим два простейших множителя (x + 1) и (x + 2). Факторизуя исходный многочлен, мы получаем его упрощенную форму (x + 1)(x + 2).
Упрощение многочленов с помощью факторизации является важным инструментом в алгебре. Оно позволяет не только упростить выражения, но и найти корни многочленов и решить уравнения, что может быть полезным при решении различных задач из математики и её приложений.
Упрощение многочленов с помощью сокращения степеней

Сокращение степеней многочлена означает устранение одинаковых степеней переменных и объединение соответствующих коэффициентов. Например, рассмотрим многочлен:
3x^2 + 5x^2 + 2x + 7x^2
В этом многочлене есть несколько одинаковых степеней переменных. Чтобы упростить его, мы должны объединить коэффициенты при одинаковых степенях.
3x^2 + 5x^2 + 2x + 7x^2 = (3 + 5 + 7)x^2 + 2x
Таким образом, многочлен можно упростить следующим образом:
15x^2 + 2x
При упрощении многочленов с помощью сокращения степеней важно обратить внимание на правильно объединение коэффициентов и сохранение правильного порядка переменных. Это позволяет получить более компактную и простую запись многочлена.
Упрощение многочленов с помощью суммирования и разложения
Метод суммирования позволяет объединить подобные слагаемые многочлена, то есть слагаемые, у которых одинаковые степени и одинаковые коэффициенты. Для этого необходимо просмотреть все слагаемые многочлена и сложить все подобные члены. Например, для многочлена 3x^2 + 2x - x^2 + 5 можно просто сложить слагаемые с одинаковыми степенями: (3x^2 - x^2) + 2x + 5, что даст окончательный результат 2x^2 + 2x + 5.
Метод разложения многочлена заключается в разбиении сложного выражения на более простые составляющие. Это может быть полезно, если многочлен содержит много слагаемых. Один из способов разложения многочлена – разложение выражения на множители или факторизация. Например, для многочлена x^2 + 5x + 6 можно разложить его на два множителя (x + 2)(x + 3).
Упрощение многочленов с помощью суммирования и разложения – важный навык в алгебре, который позволяет быстро и эффективно работать с многочленами. Эти методы могут быть использованы для нахождения корней уравнений, факторизации многочленов и других алгебраических операций.








