В математике точкой экстремума функции называется точка, в которой эта функция достигает локального максимума или минимума. Нахождение этих точек является важной задачей во многих областях, от оптимизации до физики и экономики. Для нахождения точек экстремума функции существуют различные математические принципы и методы.
Один из основных инструментов для нахождения экстремума функции - это производные. Производная функции показывает ее скорость изменения в каждой точке. Для точки экстремума производная равна нулю, что позволяет найти его аналитически. Этот метод называется аналитическим нахождением экстремума функции.
Если аналитический метод сложен или невозможен, можно воспользоваться численными методами. Они заключаются в приближенном вычислении производных или в поиске экстремума на отрезке с помощью итераций. В численных методах используются различные алгоритмы, такие как метод Ньютона, метод золотого сечения и методы оптимизации.
Важно отметить, что нахождение точек экстремума функции имеет большое практическое значение. Это помогает нам оптимизировать процессы, улучшать результаты и применять математические модели в реальной жизни. Нахождение экстремума функции - это не только математическая задача, но и инструмент для решения практических проблем.
Независимо от метода, выбранного для нахождения точек экстремума функции, это задача, требующая внимательности и ответственности. Необходимо учитывать особенности функции, ее границы и условия. Точки экстремума функции могут быть не только максимумами и минимумами, но и седловыми точками или точками перегиба. Математические принципы и методы помогают нам разобраться в этих сложных ситуациях и применить правильный подход для нахождения экстремума.
Понятие экстремума функции
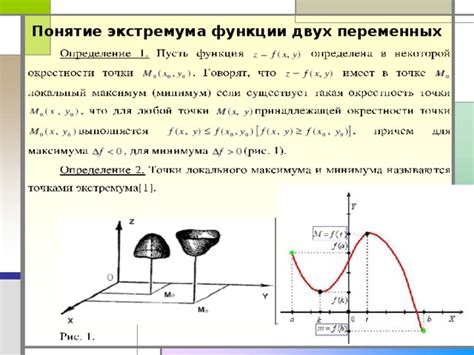
Максимум функции – это точка, в которой функция принимает наибольшее значение на заданном интервале или на всей области определения. Минимум функции – это точка, в которой функция принимает наименьшее значение на заданном интервале или на всей области определения.
Для того чтобы найти экстремумы функции, необходимо выполнить следующие шаги:
1. Найти все точки, в которых производная функции равна нулю или не существует. Эти точки называются стационарными.
2. Определить значения функции в стационарных точках и на концах заданного интервала.
3. Сравнить полученные значения и выбрать наибольшее и наименьшее из них. Эти значения представляют максимум и минимум функции соответственно.
4. Если значения функции в стационарных точках и на концах интервала совпадают или функция не определена на концах интервала, то экстремумов на заданном интервале нет.
Экстремумы функции имеют важное значение во многих областях, таких как оптимизация, экономика, физика, анализ данных и другие.
Типы экстремумов
| Тип экстремума | Описание |
|---|---|
| Локальный максимум | Точка, в которой значение функции является наивысшим в некоторой окрестности данной точки. В окрестности локального максимума значения функции возрастают до этой точки и убывают после неё. |
| Локальный минимум | Точка, в которой значение функции является наименьшим в некоторой окрестности данной точки. В окрестности локального минимума значения функции убывают до этой точки и возрастают после неё. |
| Глобальный максимум | Точка, в которой значение функции является наивысшим на всей области определения функции. Для поиска глобального максимума, требуется проанализировать весь интервал значений функции. |
| Глобальный минимум | Точка, в которой значение функции является наименьшим на всей области определения функции. Для поиска глобального минимума, требуется проанализировать весь интервал значений функции. |
Определение типа экстремума функции важно для понимания её поведения и использования в различных задачах и моделях. Для точного определения экстремумов функций применяются различные математические методы и алгоритмы, такие как производные, метод Ньютона и другие.
Математические принципы поиска экстремумов

Чтобы найти точки экстремума функции, используются основные принципы и методы, такие как производная функции, критерий экстремума, вторая производная, условия первого и второго порядка.
Одним из основных математических принципов поиска экстремумов является использование производной функции. Если производная равна нулю или не определена в точке, то существует вероятность наличия экстремума в этой точке. Это может быть точка минимума, максимума или точка перегиба.
Критерий экстремума – это необходимое условие для нахождения точек экстремума. Если функция является дифференцируемой и точка является стационарной (производная равна нулю), то можно сделать вывод о наличии экстремума в этой точке.
Вторая производная функции позволяет определить тип экстремума в точке. Если вторая производная положительна, то это указывает на наличие минимума в данной точке. Если же вторая производная отрицательна, то это указывает на наличие максимума.
Условия первого и второго порядка позволяют определить точно наличие экстремума в точке и его тип. Условие первого порядка основано на равенстве нулю производной функции, а условие второго порядка основано на знаке второй производной.
Все эти математические принципы и методы позволяют найти точки экстремума функции и определить их тип. Использование этих принципов позволяет решить множество задач и применить полученные результаты в практике.
Методы численного поиска экстремумов
Одним из наиболее распространенных численных методов является метод дихотомии. Этот метод основан на принципе деления отрезка пополам. Идея заключается в том, что если функция меняет знак на отрезке, то на этом отрезке гарантированно существует точка экстремума. Метод дихотомии последовательно делит отрезок пополам до тех пор, пока разность значений функции на концах отрезка не станет меньше заданной точности.
Еще одним распространенным методом является метод золотого сечения. Этот метод также основан на принципе деления отрезка. Он отличается от метода дихотомии тем, что отрезок делится не пополам, а в определенном пропорции. При каждом делении отбрасывается меньший из двух отрезков, так как он не содержит точку экстремума.
Также используется метод касательных, или метод Ньютона. В этом методе используется приближение к функции с помощью касательной на графике функции. На каждом шаге метода строится касательная к графику функции в точке, и точка пересечения касательной с осью абсцисс принимается за следующее приближение точки экстремума.
Методы численного поиска экстремумов широко применяются в практических задачах, когда аналитическое решение сложно или невозможно получить. Они позволяют найти приближенное значение точки экстремума с заданной точностью. Однако следует отметить, что численные методы могут быть чувствительны к выбору начального приближения и шага. Поэтому важно выбирать оптимальные параметры для каждой конкретной задачи.
Методы аналитического поиска экстремумов
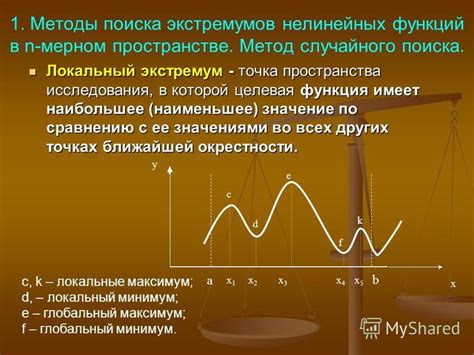
Одним из основных методов является производная функции. Производная показывает скорость изменения значения функции в каждой точке. Точка экстремума функции соответствует моменту, когда производная равна нулю или не существует. Для нахождения точек экстремума с помощью производной функции необходимо найти корни уравнения производной.
Если производная равна нулю в точке, то необходимо проверить, является ли эта точка точкой максимума, минимума или седловой. Для этого используется вторая производная. Если вторая производная положительна в точке, то эта точка является точкой минимума. Если вторая производная отрицательна, то точка является точкой максимума. Если вторая производная равна нулю или не существует, то это может быть седловая точка – точка, в которой функция имеет как максимум, так и минимум.
Однако есть и другие методы аналитического поиска экстремумов. Например, метод Лагранжа позволяет найти экстремумы с использованием условий равенства нулю всех производных функции по каждой переменной. Метод наименьших квадратов используется в задачах аппроксимации функций для нахождения экстремумов.
Важно помнить, что аналитические методы поиска экстремумов могут быть применимы только для дифференцируемых функций. Если функция не является дифференцируемой или имеет разрывы, то требуются другие методы поиска экстремумов, например, численные методы.
Градиентные методы поиска экстремумов
Процесс поиска экстремума состоит из итераций, на каждой из которых текущая точка обновляется в направлении антиградиента. Данный процесс продолжается до достижения требуемой точности или удовлетворения другому критерию остановки. В зависимости от выбранного градиентного метода, скорость сходимости и точность результата могут значительно отличаться.
Наиболее популярными градиентными методами являются:
- Метод наискорейшего спуска;
- Метод сопряженных градиентов;
- Метод Ньютона;
- Метод Левенберга-Марквардта;
- Метод Бройдена-Флетчера-Гольдфарба-Шанно.
Каждый из этих методов имеет свои особенности и применяется в зависимости от требуемой точности, размерности задачи и свойств функции. Например, метод наискорейшего спуска хорошо подходит для функций с выпуклым и однородным ландшафтом, тогда как метод сопряженных градиентов позволяет эффективно решать задачи с квадратичными функциями.
Методы многомерной оптимизации
Одним из наиболее часто используемых методов многомерной оптимизации является метод градиентного спуска. Он основан на понятии градиента функции, который указывает направление наибольшего роста функции. В методе градиентного спуска ищется точка экстремума путем последовательного движения в направлении, противоположном градиенту функции.
Другим методом многомерной оптимизации является метод Ньютона. Он основан на идее аппроксимации функции в окрестности точки экстремума с помощью квадратичной функции. Метод Ньютона находит точку экстремума путем решения системы нелинейных уравнений, полученных из квадратичной аппроксимации функции.
Метод сопряженных градиентов является еще одним эффективным методом многомерной оптимизации. Он основан на идее использования направлений, сопряженных к предыдущим направлениям спуска, для быстрого приближения к точке экстремума функции.
Кроме того, существует множество других методов многомерной оптимизации, таких как методы роя частиц, генетические алгоритмы, методы квазиньютоновского типа и др. Каждый из них имеет свои особенности и применяется в зависимости от задачи оптимизации.
Применение эволюционных алгоритмов для поиска экстремумов

Идея эволюционных алгоритмов заключается в том, что решения представлены в виде генетических кодов, которые могут быть изменены и комбинированы с помощью операторов мутации и скрещивания. Таким образом, создается популяция потенциальных решений, которая эволюционирует с течением времени.
Основными компонентами эволюционных алгоритмов являются:
| Компонент | Описание |
|---|---|
| Популяция | Множество потенциальных решений, представленных генетическими кодами. |
| Функция приспособленности | Критерий, по которому оценивается качество каждого решения в популяции. |
| Оператор мутации | Позволяет изменить генетический код решения для получения нового потенциального решения. |
| Оператор скрещивания | Позволяет комбинировать генетический код двух решений для создания нового потенциального решения. |
| Отбор | Процесс, в ходе которого из популяции выбираются наиболее приспособленные решения. |
| Параметры | Параметры алгоритма, такие как размер популяции, вероятность мутации и скрещивания и т. д. |
Применение эволюционных алгоритмов для поиска экстремумов позволяет обойти проблемы, связанные с применением классических методов оптимизации, таких как градиентный спуск. Эти алгоритмы позволяют находить глобальные экстремумы функций, а не только локальные, что делает их особенно полезными в задачах с нетривиальной геометрией функций.
Одним из наиболее популярных эволюционных алгоритмов для поиска экстремумов является генетический алгоритм. Он применяется в различных областях науки и техники, таких как оптимизация параметров нейронных сетей, проектирование оптимальных структур и т. д.
В заключение, применение эволюционных алгоритмов для поиска экстремумов функций является эффективным способом решения сложных оптимизационных задач. Эти алгоритмы позволяют найти глобальные экстремумы и обойти проблемы, связанные с локальными оптимумами. Их гибкость и широкий спектр применения делают их важным инструментом для исследователей и инженеров во многих областях.









