Задача коши – ключевая задача дифференциального исчисления, которая связывает необходимость определения решения дифференциального уравнения с начальными условиями. Ее решение играет важную роль во многих областях математики, физики и инженерии.
Одним из основных принципов решения задачи коши является учет начальных условий, которые задаются в виде значений функции и ее производной в определенной точке. Эти условия позволяют найти конкретное решение исходного дифференциального уравнения, удовлетворяющее данным условиям.
Существует множество методов решения задачи коши для дифференциальных уравнений. Одним из наиболее распространенных методов является метод Эйлера, который основан на аппроксимации итерационным процессом. Он позволяет численно вычислить значения функции на заданном интервале и найти ее значение в точке, которая не задана начальными условиями.
Если говорить о более точных методах решения задачи коши, то следует упомянуть метод Рунге-Кутты и метод сшивки граничных условий. Метод Рунге-Кутты обеспечивает более точное приближенное решение, используя несколько итераций для каждого шага интервала. Он позволяет получить приближенное решение с заданной точностью.
В заключение, решение задачи коши для дифференциального уравнения является важной задачей математики и имеет множество применений. Оно позволяет находить конкретное решение дифференциального уравнения, удовлетворяющее начальным условиям, и численно определить значение функции в любой точке интервала. Методы решения задачи коши позволяют получить приближенные решения с заданной точностью и являются непременным инструментом в научном и инженерном исследовании.
Определение и примеры

Формально задача коши для дифференциального уравнения выглядит следующим образом:
Дано: дифференциальное уравнение вида F(x, y, y', ..., y(n)) = 0, где y(x), y'(x), ..., y(n)(x) – искомая функция и ее производные относительно переменной x.
Дано: начальные условия вида y(x0) = y0, y'(x0) = y'0, ..., y(n-1)(x0) = y(n-1)0, где x0, y0, y'0, ..., y(n-1)0 – известные значения функции и ее производных для некоторого начального значения переменной x, обычно заданного при x = x0.
Решением задачи коши является функция y(x), которая удовлетворяет дифференциальному уравнению и начальным условиям с данными значениями.
| Пример | Уравнение и начальные условия | Решение |
|---|---|---|
| 1 | y' = -2xy, y(0) = 1 | y(x) = e-x2 |
| 2 | y'' + y = 0, y(0) = 0, y'(0) = 1 | y(x) = sin(x) |
| 3 | y'' - 4y = 0, y(0) = 2, y'(0) = 1 | y(x) = 2e2x + e-2x |
В примерах приведены решения задач коши для различных дифференциальных уравнений. В каждом случае указано уравнение и начальные условия, а также найдено решение в виде явной функции y(x).
Принципы решения задачи коши
Задача коши для дифференциального уравнения состоит в нахождении функции, удовлетворяющей заданному уравнению и начальным условиям. Данная задача возникает при изучении процессов, где состояние системы зависит от текущего момента времени и начального состояния.
Основными принципами решения задачи коши являются:
- Существование и единственность решения: Для задачи коши необходимо доказать, что существует единственная функция, удовлетворяющая уравнению и начальным условиям. Для этого обычно применяются математические теоремы, такие как теорема о существовании и единственности решения дифференциального уравнения.
- Первый шаг метода: Первым шагом при решении задачи коши является приведение дифференциального уравнения к стандартному виду, где все неизвестные функции выражаются через одну переменную. Для этого могут применяться различные алгебраические или тригонометрические преобразования.
- Интегрирование уравнения: После приведения уравнения к стандартному виду производится интегрирование с целью нахождения общего решения дифференциального уравнения. При этом могут использоваться различные методы, такие как методы разделения переменных, методы замены переменных или методы Лапласа.
- Нахождение констант интегрирования: В результате интегрирования получается общее решение уравнения, включающее произвольные постоянные. Чтобы найти частное решение, необходимо использовать начальные условия, которые определяют значения функции и ее производных в заданный момент времени.
- Итоговая форма решения: После определения констант интегрирования и подстановки начальных условий получается итоговая форма решения задачи коши. Она представляет собой конкретную функцию, которая удовлетворяет заданному уравнению и начальным условиям.
Принципы решения задачи коши существенны при изучении многих физических явлений, таких как движение материальных точек, процессы в электрических цепях, динамика системы частиц и другие. Они позволяют найти функциональную зависимость, описывающую эволюцию системы во времени.
Начальные условия и решение

При решении задачи Коши для дифференциального уравнения необходимо определить начальные условия. Начальные условия представляют собой значения неизвестной функции и ее производных в определенной точке.
Задача Коши описывает эволюцию физической системы и включает в себя математическую модель в виде дифференциального уравнения и начальные условия. Решение задачи Коши позволяет определить значения функции в любой момент времени.
Для решения задачи Коши используются различные методы. Один из наиболее распространенных методов – метод Эйлера. Суть метода заключается в аппроксимации производной функции с помощью конечной разности. Этот метод позволяет приближенно решать дифференциальные уравнения численно.
Процесс решения задачи Коши включает в себя следующие шаги:
| 1 | Определение дифференциального уравнения и начальных условий. |
| 2 | Выбор метода решения задачи Коши. |
| 3 | Аппроксимация значения функции и ее производной с помощью выбранного метода. |
| 4 | Проверка полученного решения путем сравнения с аналитическим решением, если оно известно. |
| 5 | Повторение шагов 3-4 для различных значений времени. |
В результате решения задачи Коши получается набор значений функции в различные моменты времени. Эти значения могут быть представлены в виде графика функции. График позволяет визуально оценить изменение функции в течение времени и сделать выводы о ее поведении.
Единственность решения
Формально, пусть задано дифференциальное уравнение вида:
F(x, y, y', ..., y(n)) = 0,
где F - некоторая функция, зависящая от переменных x, y, y', ..., y(n), и y(k) обозначает k-ю производную функции y по переменной x.
Задача Коши для этого уравнения состоит в нахождении функции y(x), удовлетворяющей уравнению и некоторым начальным условиям:
y(x0) = y0, y'(x0) = y'0, ..., y(n-1)(x0) = y(n-1)0.
Теорема о единственности решения гарантирует, что если функция y(x) является решением задачи Коши, то она является единственным решением с учетом заданных начальных условий.
Для дифференциальных уравнений первого порядка единственность решения следует из теоремы Пеано о существовании решения. Для дифференциальных уравнений более высоких порядков единственность решения доказывается с помощью метода Лиувилля.
Методы решения задачи коши

Для решения задачи коши существует несколько методов, каждый из которых имеет свои преимущества и ограничения. Некоторые из наиболее распространенных методов включают:
Метод Эйлера: это один из самых простых и наиболее распространенных методов решения задачи коши. Он основывается на аппроксимации решения в каждой точке с помощью линейной функции, и обладает низкой точностью, особенно при большом шаге. Метод Эйлера является явным методом, что означает, что значения в следующей точке вычисляются исходя из значений в предыдущей точке.
Метод Рунге-Кутта: данный метод является улучшением метода Эйлера и позволяет значительно повысить точность вычислений. Метод Рунге-Кутта также является явным методом и имеет различные порядки точности, в зависимости от выбранных параметров. Это делает его более гибким и эффективным инструментом для решения задачи коши.
Метод Адамса: данный метод является неявным методом, что означает, что значения в следующей точке вычисляются с использованием значений в предыдущих точках. Метод Адамса также имеет различные порядки точности, и он обладает высокой стабильностью и точностью даже при большом шаге. Однако, он требует более сложных вычислений по сравнению с явными методами.
Все эти методы основаны на различных приближениях решения задачи коши. Выбор конкретного метода зависит от требуемой точности, устойчивости и вычислительной сложности. Часто применяются комбинации различных методов для достижения наилучшего результата.
Метод разложения по рядам
Идея метода заключается в том, что неизвестная функция разлагается в ряд Тейлора или Фурье, и полученное разложение подставляется в исходное дифференциальное уравнение. Затем используются свойства рядов и принципы представления функций в виде суммы рядов для определения коэффициентов разложения и решения задачи Коши.
Процесс разложения по рядам может быть довольно сложным и требует математических навыков для работы с рядами и дифференциальными уравнениями. Однако, этот метод позволяет получать аналитическое решение задачи Коши в виде ряда, что может быть полезно для анализа свойств решений и проведения численных исследований.
Также стоит отметить, что метод разложения по рядам имеет ограниченную область применения. Не все дифференциальные уравнения могут быть решены с помощью этого метода, и в некоторых случаях разложение по рядам может быть слишком сложным или сходиться очень медленно.
В заключение, метод разложения по рядам является одним из важных инструментов при аналитическом решении дифференциальных уравнений. Он позволяет получить аналитическое решение в виде ряда, что может быть полезно для дальнейшего анализа уравнений и проведения численных исследований. Однако, необходимо учитывать ограничения этого метода и выбирать другие методы решения в случае, если разложение по рядам не применимо.
Метод последовательных приближений
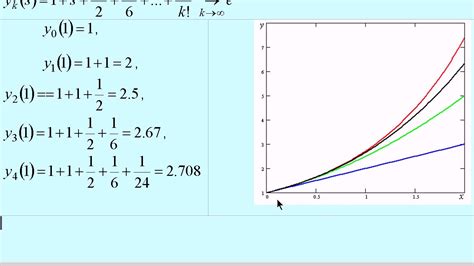
В основе метода лежит идея замены исходного уравнения более простым, но приближенным уравнением, решение которого можно найти аналитически или численно. Затем найденное решение используется в качестве начального значения для решения более точного приближенного уравнения.
Процесс повторяется многократно до тех пор, пока не будет достигнута требуемая точность. В результате получается последовательность приближений, сходящихся к точному решению задачи Коши.
Метод последовательных приближений широко используется для решения дифференциальных уравнений, таких как уравнение Лапласа, уравнение Пуассона, уравнение теплопроводности, а также в физических и инженерных задачах. Однако следует учитывать, что метод может быть применен только при выполнении определенных условий на исходное уравнение и начальные условия.
Метод вариации постоянных
Применение метода вариации постоянных позволяет найти частное решение дифференциального уравнения, удовлетворяющее дополнительным условиям задачи Коши. Этот метод позволяет снизить задачу нахождения решения дифференциального уравнения к решению системы алгебраических уравнений.
Шаги метода вариации постоянных:
- Найдите общее решение дифференциального уравнения.
- Подставьте в общее решение функцию, содержащую произвольные постоянные, и обозначьте эти постоянные новыми символами.
- Найдите производные этой функции и подставьте их в исходное дифференциальное уравнение.
- Составьте систему уравнений, связывающую новые символы с коэффициентами исходного уравнения.
- Решите эту систему уравнений и найдите значения произвольных постоянных.
- Подставьте найденные значения постоянных в функцию и получите частное решение дифференциального уравнения, удовлетворяющее начальным условиям.
Метод вариации постоянных является удобным инструментом решения задачи Коши для дифференциального уравнения. Он позволяет найти специфическое решение, удовлетворяющее дополнительным условиям, заданным в начальной точке. Этот метод находит широкое применение в различных областях науки и техники, где требуется решить задачу с заданными начальными условиями.








