Решение системы неравенств является важной задачей в математике, а также во многих областях науки и техники. Система неравенств представляет собой набор неравенств, которые должны быть выполнены одновременно. Решение системы неравенств – это множество значений переменных, при которых все неравенства выполняются.
Существует несколько методов для решения систем неравенств, включая графический метод, метод подстановки и метод исключения переменных. Однако наиболее общий и эффективный способ решения систем неравенств – это использование алгебраических методов и правил, которые позволяют найти все возможные значения переменных системы.
При решении системы неравенств необходимо учитывать основные правила алгебры, такие как закон сохранения неравенства при умножении или делении на положительное число, а также знак неравенства при умножении или делении на отрицательное число.
Кроме того, при решении системы неравенств может потребоваться использование понятия интервала – отрезка числовой прямой, который содержит все определенные значения переменной. Интервалы могут быть открытыми, закрытыми или полуоткрытыми, что влияет на решение системы неравенств и определение ее множества решений.
Что такое система неравенств?

Система неравенств может содержать как знаки строгого неравенства (), так и знаки нестрогого неравенства (≤, ≥). Цель решения системы неравенств состоит в определении набора значений переменных, которые удовлетворяют всем неравенствам системы.
Важно отметить, что решением системы неравенств может быть набор чисел или интервалы значений, а не конкретные числа. Например, решением системы может быть набор x ∈ (-∞, 3] ∪ (6, ∞), что означает, что x может быть любым числом меньше или равным 3, или любым числом больше 6.
Для решения системы неравенств необходимо использовать различные методы и приемы алгебры, а также анализировать условия и взаимосвязи между неравенствами в системе. Иногда решение системы может быть представлено в виде графика на числовой оси.
Понимание системы неравенств и умение решать ее является важным навыком в математике, который находит применение во многих областях, включая экономику, физику и программирование.
Методы решения системы неравенств
Графический метод
Один из способов решения системы неравенств – графический метод. Для этого строятся графики каждого неравенства системы на координатной плоскости и определяется область, в которой пересекаются все графики. Решением системы неравенств будет множество всех точек, удовлетворяющих этой области.
Метод подстановки
Другим методом решения системы неравенств является метод подстановки. В этом методе из одного неравенства системы выражают одну переменную через остальные и подставляют это выражение во все остальные неравенства. Затем решается полученное уравнение, и найденное значение переменной подставляется в исходные неравенства для определения остальных переменных. После этого проверяются полученные значения на совместность или несовместность системы.
Метод последовательного исключения переменных
Метод последовательного исключения переменных применяется для систем неравенств с более чем двумя переменными. В этом методе из каждого неравенства системы последовательно исключается по одной переменной до тех пор, пока не останется одно неравенство с одной переменной. Затем это уравнение решается, и значение найденной переменной подставляется в исходные неравенства для определения значений остальных переменных.
Метод линейного программирования
Метод линейного программирования применяется для решения систем неравенств, если требуется найти такие значения переменных, при которых достигается максимальное или минимальное значение линейной функции. Он основан на использовании понятий ограничений и целевой функции.
Метод замены переменных
Метод замены переменных позволяет свести систему неравенств к более простой форме. В этом методе вводятся новые переменные, которые заменяют исходные переменные, и получается система уравнений. Затем решается эта система, и найденные значения новых переменных подставляются в исходные неравенства для определения значений исходных переменных.
Метод исключения неопределенности
Метод исключения неопределенности применяется для систем неравенств, в которых имеется неопределенный знак (неравенство типа «»). В этом методе заменяют все неопределенные знаки соответствующими строгим знаками (неравенство типа «≤», «≥») и решают полученную систему неравенств.
Метод логарифмирования
Метод логарифмирования используется для решения систем неравенств, содержащих логарифмические выражения. В этом методе выражения с логарифмами преобразуются в уравнения, решаются, и найденные значения подставляются в исходные неравенства.
При решении системы неравенств важно помнить о важности проверки полученных решений и областей их существования. Некорректное применение методов может привести к ошибкам и неправильным результатам. Поэтому рекомендуется сначала освоить простые системы неравенств, а затем продолжать решать более сложные задачи.
Метод графиков
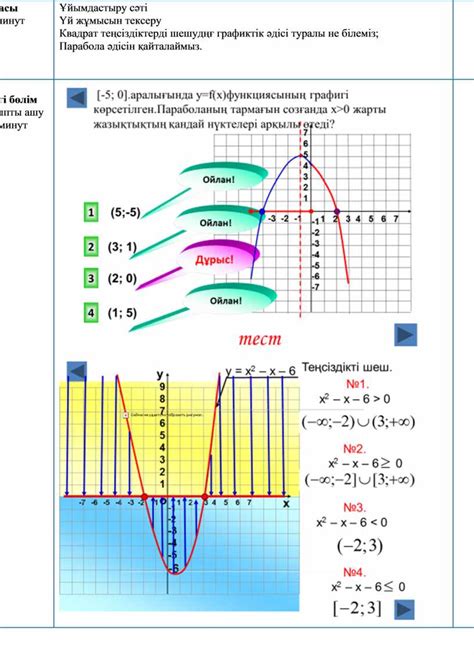
Для решения системы неравенств методом графиков необходимо выполнить следующие шаги:
- Задать неравенства в виде уравнений.
- Построить графики каждого уравнения на плоскости.
- Определить области, в которых выполняются неравенства, и выделить их на графике.
- Найти точки пересечения графиков, которые представляют собой решения системы неравенств.
Для построения графиков уравнений и определения областей решений удобно использовать координатную плоскость. При этом неравенство типа "меньше" представляется полупрямой, направленной влево или вниз от графика уравнения, а неравенство типа "больше" - полупрямой, направленной вправо или вверх от графика уравнения.
Используя метод графиков, можно наглядно представить все возможные решения системы неравенств и определить их количество и характер. Однако этот метод может быть неэффективен для систем с большим числом уравнений и переменных, так как построение графиков становится сложным и трудоемким процессом.
| Пример | График |
|---|---|
| Система неравенств: 2x + y ≤ 5 x - y > 1 |  |
В данном примере, решением системы неравенств является область, закрашенная на графике. Она представляет собой область пересечения полуплоскостей, определенных первым и вторым уравнениями системы.
Метод подстановки
Шаги метода подстановки:
- Выбираем одно уравнение из системы неравенств.
- Выбираем переменную, которой будем подставлять значения.
- Подставляем в выбранное уравнение значение переменной и решаем получившееся уравнение.
- Полученное значение переменной подставляем в остальные уравнения системы и находим значения других переменных.
- Проверяем полученное решение, подставляя его в исходные неравенства системы.
- Если все исходные неравенства выполняются при найденных значениях переменных, то это решение системы неравенств.
- Если хотя бы одно из исходных неравенств не выполняется при найденных значениях переменных, то полученное решение не является решением системы неравенств.
Преимуществом метода подстановки является его простота и понятность. Однако он может быть неэффективным для систем большой размерности или с большим количеством переменных. В таких случаях целесообразно использовать другие методы, например, графический метод или метод исключения.
Метод приведения к двойственной системе

Шаги метода приведения к двойственной системе:
- Записываем исходную систему неравенств в стандартной форме.
- Выбираем вспомогательные переменные и добавляем их к исходной системе. Количество вспомогательных переменных должно быть равно количеству неравенств.
- Меняем знаки неравенств в исходной системе на противоположные.
- Заменяем исходные переменные исключительно с вспомогательными переменными.
- Полученную двойственную систему решаем методом, удобным для данной задачи (например, методом Гаусса или методом простых итераций).
- После нахождения решений двойственной системы выполняем обратные замены и получаем все решения исходной системы неравенств.
Метод приведения к двойственной системе является универсальным и применим для различных видов систем неравенств. Он позволяет решить систему неравенств и найти все ее решения, включая крайние точки.
Алгебраический подход к решению системы неравенств
Основная идея алгебраического подхода заключается в том, чтобы привести систему неравенств к эквивалентной системе уравнений, которую уже легче решить. Для этого используются следующие шаги:
| Шаг | Описание |
|---|---|
| 1 | Представить все неравенства в виде линейных выражений (например, заменить знаки неравенств на знаки равенства) |
| 2 | Решить полученную систему уравнений |
| 3 | Проверить полученные решения на соответствие исходным неравенствам |
Если по результатам шага 2 было получено бесконечное число решений, то это значит, что система неравенств имеет бесконечное число решений. Если же полученное множество решений пустое, то система неравенств не имеет решений.
Алгебраический подход к решению системы неравенств может быть очень полезным, особенно при работе с большим количеством неравенств. Он позволяет легко и систематично решать такие системы, избегая ошибок и упусков.
Использование матриц и векторов

Для решения системы неравенств и поиска всех ее решений может быть полезным использовать понятия матриц и векторов. Матрицы и векторы представляют собой мощные инструменты для организации и работы с большими наборами данных.
Систему неравенств можно представить в виде матрицы, где каждое уравнение системы будет строкой матрицы. Каждое уравнение содержит коэффициенты переменных и значение, к которому оно ограничено. Затем можно использовать методы матричной алгебры для решения системы.
Векторы могут быть использованы для представления решений системы неравенств. Каждый вектор представляет собой точку, которая удовлетворяет всем ограничениям системы. Путем комбинирования векторов можно найти все возможные решения системы.
Использование матриц и векторов является эффективным способом решения систем неравенств, особенно когда количество переменных или уравнений становится слишком большим. Они позволяют упростить вычисления и найти все решения системы без необходимости рассмотрения каждого уравнения отдельно.
Примечание: Обратите внимание, что для использования матриц и векторов требуется некоторое математическое знание и понимание алгебры.
Применение метода Гаусса
Для решения системы неравенств методом Гаусса необходимо следующие шаги:
- Записать систему неравенств в виде расширенной матрицы. В этой матрице уравнения располагаются по строкам, а свободные члены – в последнем столбце.
- Привести матрицу к ступенчатому виду, используя элементарные преобразования строк. Элементарные преобразования включают сложение строк, умножение строки на число и перестановку строк.
- Выразить неизвестные через свободные члены. Это делается путем обратного хода от последней строки матрицы к первой.
- Проверить полученные значения неизвестных, подставив их в исходные неравенства. Если все неравенства выполняются, то найденное решение является корректным. Если хотя бы одно неравенство не выполняется, то система неравенств не имеет решений.
Преимущества метода Гаусса заключаются в его универсальности и простоте применения. Он может быть использован для решения систем неравенств любого размера и типа. Кроме того, этот метод позволяет найти все решения системы неравенств, если они существуют.
Решение системы с помощью линейного программирования
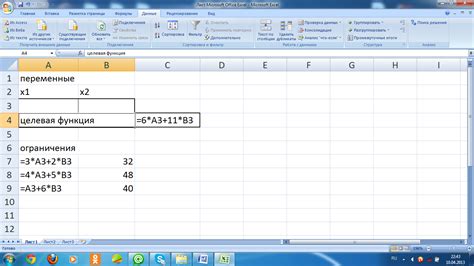
Для решения системы неравенств с помощью линейного программирования необходимо выполнить следующие шаги:
- Записать систему неравенств в виде линейной комбинации переменных, где переменные являются неотрицательными.
- Сформулировать целевую функцию, которую нужно оптимизировать. В качестве целевой функции может быть выбрана сумма переменных или их произведение.
- Ограничения задаются неравенствами, которые нужно преобразовать в равенства с помощью добавления новых переменных.
- Найти оптимальное решение задачи линейного программирования с помощью известных методов, таких как метод симплекс-алгоритма или метод ветвей и границ.
- Получить решения системы неравенств из найденного оптимального решения, учитывая условия на неотрицательность переменных.
Таким образом, использование линейного программирования позволяет эффективно находить все решения системы неравенств. Этот метод является мощным инструментом для решения задач оптимизации и нахождения наилучших вариантов решений.
Нахождение всех решений системы неравенств
Для решения системы неравенств существует несколько методов, включая графический и алгебраический подходы. Графический подход заключается в построении графиков неравенств и определении областей, где графики пересекаются. Алгебраический подход включает в себя применение различных алгебраических методов, таких как метод подстановки и метод исключения.
При нахождении всех решений системы неравенств важно учитывать граничные условия и особые случаи. Например, при решении системы линейных неравенств необходимо проверить случаи, когда некоторые переменные приравниваются к нулю или крайним значениям. Это позволяет нам определить, находятся ли точки на границе решения или внутри него.
Помимо графического и алгебраического подходов, также существуют численные методы для решения систем неравенств, такие как методы оптимизации. Эти методы позволяют найти приближенные значения решений системы неравенств, которые удовлетворяют определенным условиям оптимальности.
Важно отметить, что каждый метод имеет свои преимущества и ограничения, и выбор метода зависит от особенностей конкретной системы неравенств и требуемой точности решений.
В заключение, нахождение всех решений системы неравенств является важным шагом в математике и инженерии. Графический, алгебраический и численный подходы позволяют определить области, в которых выполняются все неравенства, и учесть граничные условия и особые случаи.
Определение границ области решений

Для решения системы неравенств необходимо определить область, в которой все неравенства выполняются одновременно. Эта область называется областью решений или границами области решений.
Чтобы определить границы области решений, нужно рассмотреть каждое неравенство системы по отдельности и найти его график на координатной плоскости.
График каждого неравенства представляет собой множество точек, которые удовлетворяют данному неравенству.
Подобные множества точек для всех неравенств пересекаются, образуя область решений системы неравенств.
Границы области решений могут быть представлены отрезками или полупрямыми на координатной плоскости.
Выделение границ области решений позволяет наглядно представить все возможные значения переменных, удовлетворяющие системе неравенств.








