Производная — это одно из ключевых понятий математического анализа, которое позволяет узнать, как быстро меняется функция в каждой точке своего определения. Продифференцировать функцию означает найти её производную, то есть выразить её изменение по отношению к изменению одной из переменных, от которых она зависит.
На практике нахождение производной позволяет решать множество задач, включая определение экстремумов функций, нахождение касательной к кривой, исследование поведения функций и т. д. В данной статье мы разберем основные правила дифференцирования и покажем, как их применять при нахождении производной различных функций.
Важно помнить, что дифференцирование требует тщательности и точности в вычислениях. Поэтому следует внимательно применять правила дифференцирования и проверять полученные результаты.
Перед тем как приступить к дифференцированию функции, необходимо понимать основные правила дифференцирования и уметь применять их для различных типов функций. Мы рассмотрим основные правила дифференцирования, такие как линейность, степенное правило, правило произведения, правило частного, правило сложной функции и другие. После этого приступим к примерам дифференцирования различных функций, чтобы показать практическое применение этих правил.
Что такое дифференцирование?

Процесс дифференцирования может быть представлен как нахождение предела отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю. В математической записи, если функция f(x) дифференцируема, то ее производная f'(x) равна пределу:
| f'(x) = lim | Δx → 0 | Δf(x) | / Δx |
где Δf(x) - приращение функции, а Δx - приращение аргумента.
Производная функции показывает, как функция меняется в каждой точке. Если производная положительна, то функция возрастает, если отрицательна - убывает, а если равна нулю - достигает экстремума.
Знание дифференцирования позволяет решать множество задач, связанных с оптимизацией, нахождением экстремумов, определением наклона кривых и многое другое. Поэтому оно является неотъемлемой частью математического анализа и имеет широкое применение в различных областях науки и техники.
Определение понятия
Производная функции может иметь различные интерпретации. Например, в физике производная функции показывает скорость изменения физической величины. В экономике производная функции может интерпретироваться как предельная норма замещения. В общем случае, производная функции используется для анализа поведения функции вблизи конкретной точки.
Зачем нужно дифференцировать функцию?
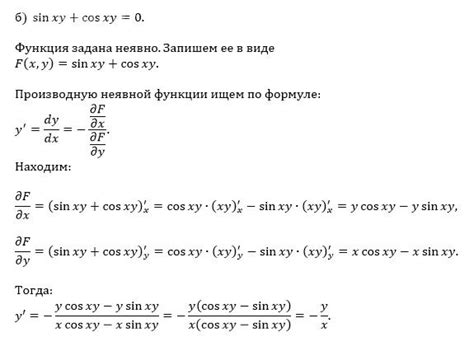
Основное применение дифференцирования состоит в решении задач, связанных с оптимизацией, определением экстремумов функций, анализом траекторий движения тел и многими другими. Например, в экономике дифференцирование используется для определения максимального прибыльного уровня производства, в физике - для моделирования движения тела под действием силы, а в машинном обучении - для настройки параметров модели.
Дифференцирование также позволяет аппроксимировать сложные функции простыми моделями, что упрощает их анализ и позволяет получать более точные результаты. Особенно важно дифференцирование при работе с функциями, заданными аналитически или в виде таблиц, графиков или экспериментальных данных.
Кроме того, понимание процесса дифференцирования и умение находить производные функций помогают развить логическое мышление, улучшить математическую эрудицию и повысить абстрактное мышление. Это важные навыки для студентов и исследователей во многих областях знания.
Как продифференцировать функцию?
Существует несколько методов для продифференцирования функций:
- Использование правил дифференцирования: существуют определенные правила, по которым можно записать дифференциалы для различных функций, например, правило суммы, правило произведения, правило применения элементарных функций и др. Эти правила позволяют нам вычислять производную функции, не обращаясь к определению дифференциала.
- Использование определения производной: альтернативный метод заключается в использовании определения производной. Согласно определению, производная функции f(x) в точке x равна предельному значению отношения изменения функции к изменению аргумента, когда эти изменения стремятся к нулю. Этот метод требует больше усилий и математических навыков, но может быть полезным для понимания процесса дифференцирования.
- Использование формул дифференцирования: существуют также стандартные формулы и табличные значения производных для некоторых базовых функций. Эти формулы позволяют нам вычислять производные функций, используя заранее известные значения производных базовых функций.
В зависимости от сложности функции и доступных средств, выбор метода продифференцирования может варьироваться. Важно быть внимательным и тщательно проводить вычисления, чтобы избежать ошибок.
Используя правила дифференцирования, определение производной или формулы дифференцирования, вы можете продифференцировать функцию и найти её производную. Это позволит вам более глубоко изучить свойства и поведение функции в заданных точках и упростить вычисления в различных математических задачах.
Основные правила дифференцирования
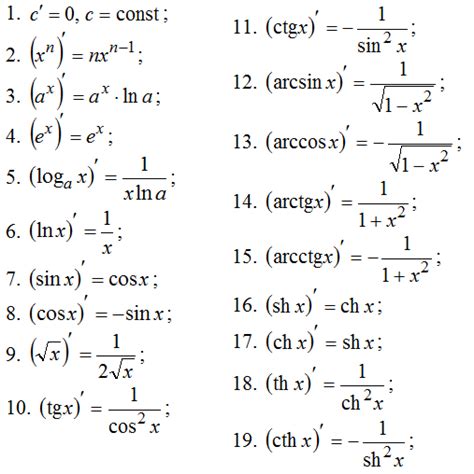
Основные правила дифференцирования включают:
| Правило | Пример |
|---|---|
| Правило линейности | \((k \cdot f(x))' = k \cdot f'(x)\) |
| Правило суммы | \((f(x) + g(x))' = f'(x) + g'(x)\) |
| Правило произведения | \((f(x) \cdot g(x))' = f'(x) \cdot g(x) + f(x) \cdot g'(x)\) |
| Правило частного | \(\left(\frac{f(x)}{g(x)} ight)' = \frac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{(g(x))^2}\) |
| Правило композиции | \((f(g(x)))' = f'(g(x)) \cdot g'(x)\) |
| Правило степени | \((x^n)' = n \cdot x^{n-1}\) |
Эти правила позволяют дифференцировать широкий спектр функций, включая линейные, полиномиальные, тригонометрические, экспоненциальные и логарифмические функции. Они могут использоваться как отдельно, так и в комбинации для нахождения производной сложных функций.
Примеры дифференцирования
Пример 1:
Пусть дана функция f(x) = 2x^2 + 3x + 1. Найдем производную этой функции.
Применим правило дифференцирования многочлена: производная каждого члена многочлена равна производной этого члена.
Таким образом, производная функции f(x) будет равна:
f'(x) = (2*2)x^(2-1) + (3*1)x^(1-1) + 0 = 4x + 3
Пример 2:
Пусть дана функция g(x) = sin(x) + cos(x). Найдем производную этой функции.
Применим правило дифференцирования синуса и косинуса: производная синуса равна косинусу, а производная косинуса равна минус синусу.
Таким образом, производная функции g(x) будет равна:
g'(x) = cos(x) - sin(x)
Пример 3:
Пусть дана функция h(x) = e^x. Найдем производную этой функции.
Применим правило дифференцирования экспоненты: производная экспоненты равна самой экспоненте.
Таким образом, производная функции h(x) будет равна:
h'(x) = e^x
Это лишь некоторые примеры дифференцирования функций. В общем случае, чтобы найти производную функции, нужно применить соответствующее правило дифференцирования в зависимости от вида функции.
Что такое производная?

Производная функции дает информацию о наклоне касательной к графику функции в каждой точке. Если производная положительна в какой-то точке, то функция возрастает в этой точке, а если производная отрицательна, то функция убывает. Если производная равна нулю, то функция имеет экстремум (максимум или минимум) в этой точке.
Производную можно использовать для решения различных задач: нахождения экстремумов функции, определения момента, когда функция достигает своего максимального или минимального значения, и других важных значений. Производная также помогает изучить форму графика функции и исследовать ее поведение.
Определение понятия
Геометрический смысл производной
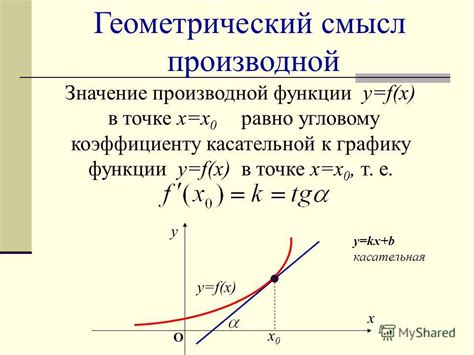
Производная функции имеет геометрическую интерпретацию, которая позволяет нам понять, как меняется функция в каждой точке своей области определения.
Графически геометрический смысл производной можно представить с помощью касательной к кривой функции в данной точке.
Если значение производной положительно, то касательная к графику функции будет подниматься, если значения производной отрицательны, то касательная будет опускаться. Если значение производной равно нулю, то касательная будет горизонтальной и функция будет иметь экстремум в данной точке.
Таким образом, производная функции позволяет нам определить прирост функции в каждой точке и выяснить, в каком направлении изменяется эта функция.
Как найти производную функции?
Существует несколько способов нахождения производной функции. Один из самых распространенных методов - использование формул дифференцирования, которые позволяют найти производную функции для различных типов функций.
Чтобы найти производную функции, необходимо выполнить следующие шаги:
- Определить тип функции (линейная, квадратичная, тригонометрическая и др.);
- Используя соответствующую формулу дифференцирования, записать функцию в виде производной;
- Упростить полученную производную функцию при необходимости;
- Вычислить значение производной функции в заданной точке или оставить ее в виде алгебраического выражения, если требуется.
При нахождении производной функции также необходимо учитывать особенности каждого типа функций, например, использование правил дифференцирования для функций вида сумма, разность, произведение, частное функций.
Нахождение производной функции является важной частью математического анализа и применяется в различных областях, таких как физика, экономика, инженерия и др. Понимание производной функции позволяет более точно моделировать и предсказывать изменения величин, описываемых функциями.
Методы нахождения производной

- Метод дифференцирования по определению. Этот метод основан на определении производной как предела отношения изменения функции к изменению ее аргумента. С его помощью можно найти производную функции прямым вычислением предела.
- Методы дифференцирования элементарных функций. Для некоторых классов функций существуют таблицы производных, которые содержат значения производных для различных элементарных функций. С их помощью можно найти производные сложных функций, применяя правила дифференцирования.
- Методы дифференцирования сложных функций. Если известны производные составляющих функций, то можно применить правила дифференцирования сложных функций, такие как правило производной композиции или правило производной обратной функции, для нахождения производных сложных функций.
- Дифференцирование неявных функций. Некоторые функции задаются неявно, то есть в виде уравнений. Для нахождения их производных можно применить метод неопределенных коэффициентов или метод дифференциалов. Они позволяют выразить производные неявных функций через производные известных функций.
- Прочие методы. Также существует ряд специализированных методов для нахождения производной, таких как метод конечных разностей, метод численного дифференцирования или метод Де Хопиталя. Они применяются в случаях, когда применение других методов затруднено или невозможно.
Выбор метода для нахождения производной зависит от конкретной функции и ее свойств. В некоторых случаях может потребоваться комбинирование разных методов для достижения результата.








