Продифференцирование функции – это математическая операция, которая позволяет найти производную функции по ее аргументу. Производная функции показывает, как функция изменяется в зависимости от изменения ее аргумента. Важно понимать, что производная функции определена для каждого ее значения и позволяет узнать, на сколько быстро меняется функция в данной точке.
Продифференцирование имеет множество практических применений. Например, оно позволяет определить скорость и ускорение движения тела, решать задачи оптимизации, находить экстремумы функций и многое другое. Кроме того, производная функции является одним из основных понятий дифференциального исчисления и служит основой для построения интеграла.
Для того чтобы найти производную функции, необходимо взять ее дифференциал и разделить его на дифференциал аргумента. Процесс продифференцирования может быть сложным и требует знания соответствующих правил и методов. Однако, существуют основные правила дифференцирования, которые позволяют находить производную большинства элементарных функций.
Продифференцирование функций играет важную роль в математике, физике, экономике, программировании и многих других областях науки и техники. Знание основных принципов и правил дифференцирования позволяет понимать и анализировать различные процессы и явления, а также решать разнообразные задачи, связанные с функциями и их изменениями.
Что такое продифференцирование функции?
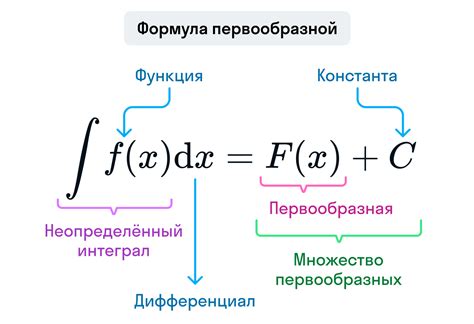
Используется математический символ 'd', записываемый перед функцией справа от знака равенства. Например, если у нас есть функция f(x), то ее производная обозначается как f'(x) или dy/dx.
Производная функции показывает скорость изменения функции в данной точке. Если производная положительна, то функция возрастает. Если производная отрицательна, функция убывает. Если производная равна нулю, то это может быть экстремум функции - максимум или минимум. Производная также может помочь понять форму функции и ее поведение в различных точках.
Продифференцирование функции широко применяется в математике, физике, экономике и других науках. Оно позволяет находить максимумы и минимумы функций, определять скорости, ускорения и другие параметры изменения величин.
Принципы продифференцирования функций
Чтобы продифференцировать функцию, необходимо использовать специальные правила дифференцирования. Существуют основные правила, которые позволяют вычислить производную более сложных функций на основе производных простых функций.
Основные принципы продифференцирования функций:
- Принцип линейности: производная линейной комбинации функций равна линейной комбинации производных этих функций. То есть, если у нас есть функции f(x) и g(x), и числа a и b, то производная функции af(x) + bg(x) равна a * f'(x) + b * g'(x). Это правило позволяет продифференцировать функции, состоящие из сложных математических выражений.
- Принцип произведения: производная произведения двух функций равна произведению производных этих функций плюс произведение первой функции на производную второй функции. То есть, если у нас есть функции f(x) и g(x), то производная от произведения f(x) * g(x) равна f'(x) * g(x) + f(x) * g'(x). Это правило позволяет продифференцировать функции, содержащие умножение.
- Принцип частного: производная частного двух функций равна разности произведения производной первой функции на вторую функцию и произведения первой функции на производную второй функции, деленной на квадрат второй функции. То есть, если у нас есть функции f(x) и g(x), то производная от частного f(x) / g(x) равна (f'(x) * g(x) - f(x) * g'(x)) / g^2(x). Это правило позволяет продифференцировать функции, содержащие деление.
- Принцип составной функции: производная составной функции равна произведению производной внешней функции и производной внутренней функции. То есть, если у нас есть функции f(x) и g(x), и функция h(x) = f(g(x)), то производная функции h(x) равна f'(g(x)) * g'(x). Это правило позволяет продифференцировать функции, состоящие из композиции других функций.
Принципы продифференцирования функций являются важными инструментами для работы с функциями и нахождения их производных. Они позволяют анализировать изменение функции в зависимости от изменения параметров и находить экстремумы, траектории движения и другие особенности функции.
Почему важно производить продифференцирование функции?

Продифференцирование особенно полезно для анализа поведения функции и определения ее важных характеристик, таких как экстремумы, точки перегиба и скорость изменения. Исследуя производную функции, мы можем определить, когда функция возрастает или убывает, где она достигает максимума или минимума, а также как функция меняет свою кривизну в разных точках.
Продифференцирование также находит широкое применение в прикладных науках, включая физику, экономику, инженерию и статистику. Например, зная производную функции, мы можем оценить скорость изменения популяции в разные моменты времени, оптимизировать производственные процессы в инженерии или анализировать рыночные тренды в экономике.
Продифференцирование также позволяет решать различные задачи оптимизации. Например, при помощи производной функции можно найти точку, в которой функция достигает максимального или минимального значения. Это важно для множества практических ситуаций, от разработки оптимальной траектории полета ракеты до осуществления прибыльной торговли на финансовых рынках.
Таким образом, продифференцирование функции играет ключевую роль в математике и позволяет нам лучше понимать и анализировать различные явления и процессы в нашем мире.
Применение продифференцирования в науке и технике
В науке продифференцирование используется во многих областях, например, в физике. Законы физики описывают изменение различных величин в пространстве и времени. Продифференцирование помогает нам понять, как эти величины меняются друг относительно друга и как их изменение влияет на окружающую среду. Например, производная скорости по времени дает нам ускорение, которое позволяет определить, насколько быстро объект изменяет свою скорость. Это основное понятие в кинематике и динамике.
В технике продифференцирование используется для решения различных инженерных задач. Например, в электротехнике мы можем использовать производную, чтобы определить интенсивность тока в цепи, вычислить мощность потребляемую различными устройствами, или определить эффективность электрических систем. В механике продифференцирование позволяет нам изучать движение механических систем и понять, как силы влияют на их состояние и поведение.
Продифференцирование также имеет широкое применение в обработке данных и в компьютерных науках. Оно используется для анализа и предсказания различных явлений, например, в финансовых рынках, в машинном обучении и искусственном интеллекте. Производные помогают нам находить экстремумы функций, определять их поведение в определенных точках и строить модели, которые могут быть использованы для прогнозирования будущих событий.
Короче говоря, продифференцирование играет важную роль в науке и технике. Оно позволяет нам изучать и описывать различные явления и процессы, а также использовать полученные знания для решения практических задач. Без продифференцирования мы были бы ограничены в нашей способности понять и контролировать окружающий мир.
Как произвести продифференцирование функции?

Для выполнения продифференцирования функции необходимо знать основные правила дифференцирования. Если функция задана явно, то ее производная может быть найдена путем применения этих правил.
Основные правила дифференцирования включают общие правила, такие как правило константы, правило суммы и правило произведения, а также специальные правила для таких элементарных функций, как степенная функция, экспоненциальная функция, логарифмическая функция и тригонометрические функции.
При продифференцировании функции необходимо записывать результат в виде новой функции, называемой производной функции. Обозначение для производной функции – f'(x), где f – исходная функция.
Знание производной функции позволяет решать различные задачи, связанные с определением тангенсовых и нормальных прямых, нахождением точек экстремума и выпуклости функции, а также анализом поведения функции на интервалах.
Важно помнить, что продифференцирование функции – это одна из основных операций математического анализа, необходимых для изучения различных явлений и процессов в физике, экономике, технике и других науках.
Основные правила и методы продифференцирования
Существуют несколько правил и методов, которые позволяют продифференцировать функцию. Ниже приведены основные из них:
1. Правило линейности:
Если f(x) и g(x) – две функции, и их производные существуют, то производная суммы f(x) + g(x) равна сумме производных функций, а производная разности f(x) - g(x) равна разности производных функций:
(f(x) + g(x))' = f'(x) + g'(x)
(f(x) - g(x))' = f'(x) - g'(x)
2. Правило произведения:
Если f(x) и g(x) – две функции, и их производные существуют, то производная их произведения равна произведению производной первой функции на вторую плюс произведение первой функции на производную второй:
(f(x) * g(x))' = f'(x) * g(x) + f(x) * g'(x)
3. Правило частного:
Если f(x) и g(x) – две функции, и их производные существуют, то производная их частного равна разности произведения производной первой функции на вторую и произведения первой функции на производную второй, делённой на квадрат второй функции:
(f(x) / g(x))' = (f'(x) * g(x) - f(x) * g'(x)) / g^2(x)
Кроме основных правил, существуют и другие методы продифференцирования, такие как правило степенной функции, правило экспоненциальной функции, правило логарифма и др. Они позволяют находить производные более сложных функций.
Знание основных правил и методов продифференцирования позволяет эффективно решать задачи по оптимизации, нахождению экстремумов функций, анализу скорости и ускорения движения и многим другим областям математики и физики.
Примеры продифференцирования функций

Процесс продифференцирования позволяет найти производную функции в каждой точке ее области определения.
Вот несколько примеров продифференцирования функций:
Пример 1: Функция f(x) = x^2
Для продифференцирования данной функции, используем правило степенной функции: при продифференцировании функции x^n, где n - любое рациональное число, производная равна n * x^(n-1).
Применяя это правило к функции f(x) = x^2, получаем: f'(x) = 2 * x^(2-1) = 2x.
Пример 2: Функция f(x) = sin(x)
Для продифференцирования данной функции, используем правило производной синуса: при продифференцировании функции sin(x), производная равна cos(x).
Применяя это правило к функции f(x) = sin(x), получаем: f'(x) = cos(x).
Пример 3: Функция f(x) = ln(x)
Для продифференцирования данной функции, используем правило производной натурального логарифма: при продифференцировании функции ln(x), производная равна 1/x.
Применяя это правило к функции f(x) = ln(x), получаем: f'(x) = 1/x.
Таким образом, продифференцирование функций позволяет найти производные и изучать их свойства в зависимости от переменной x. Это является важной операцией в математическом анализе и науках, связанных с ним.
Пример 1: продифференцирование полинома
Предположим, у нас есть полином, который задан следующим образом:
$$f(x) = a_n \cdot x^n + a_{n-1}\cdot x^{n-1} + \ldots + a_1\cdot x + a_0$$
Где $$a_n, a_{n-1}, \ldots, a_1, a_0$$ - коэффициенты полинома, а $$x$$ - переменная.
Чтобы продифференцировать полином, нужно взять производную от каждого слагаемого по отдельности. Производная слагаемого $$a_k\cdot x^k$$ равна $$a_k\cdot k\cdot x^{k-1}$$. Таким образом, получим:
$$f'(x) = a_n\cdot n\cdot x^{n-1} + a_{n-1}\cdot (n-1)\cdot x^{n-2} + \ldots + a_1$$
Таким образом, мы получили новую функцию $$f'(x)$$, которая является производной исходного полинома. Эта функция описывает изменение исходного полинома в зависимости от значения $$x$$.








