Интеграл – одно из важнейших понятий математического анализа. Однако, не все функции могут быть проинтегрированы. Некоторые из них имеют расходимость интеграла, то есть интеграл от них не существует или имеет бесконечное значение.
Интеграл расходится, когда значение интеграла для данной функции равно бесконечности. Это может произойти, если функция имеет особенности, такие как точки разрыва или бесконечное возрастание или убывание, в области интегрирования. Расходимость интеграла может указывать на то, что функция не удовлетворяет условиям существования интеграла.
Чтобы понять, почему интеграл расходится, необходимо проанализировать поведение функции в области интегрирования. Если функция имеет особенности, то возможно ее интеграл не существует. В некоторых случаях можно использовать математические методы, такие как расширение области интегрирования или представление функции в виде ряда. Однако, в большинстве случаев расходимость интеграла носит фундаментальный характер и связана с особенностями самой функции.
Пределы интегрирования и разрывы функции

Разрыв функции - это точка или диапазон значений переменной, где функция становится неопределенной или принимает бесконечное значение. Разрывы функции могут возникать из-за различных причин, например, деления на ноль или иных математических ограничений.
Интеграл расходится в случае, если функция имеет разрывы внутри интервала интегрирования. В таком случае, при подсчете интеграла, значения функции в этих разрывных точках могут приводить к неопределенным результатам или бесконечности.
Понять, что интеграл расходится из-за разрывов функции, можно, проанализировав функцию и выявив ее точки разрыва. При наличии разрывов, интеграл может быть посчитан как сумма интегралов на подинтервалах между разрывными точками, при условии, что каждый из этих подинтервалов не содержит разрывов.
Неограниченность функции на интервале интегрирования
Интеграл может расходиться, если функция, которую мы интегрируем, неограниченна на интервале интегрирования. Это означает, что значение функции стремится к бесконечности на определенной части интервала или на всем интервале.
Понять, что функция неограниченна на интервале, можно обратив внимание на различные характеристики функции, такие как ее поведение при стремлении аргумента к граничным значениям интервала или изменение знака функции внутри интервала. Если функция стремится к бесконечности или меняет знак внутри интервала, это может быть признаком неограниченности функции на интервале.
| Пример 1 | Пример 2 |
|---|---|
Функция f(x) = 1/x неограниченна на интервале (0, 1), так как значение функции стремится к бесконечности при стремлении x к нулю. В результате, интеграл от этой функции на интервале (0, 1) будет расходиться. | Функция f(x) = cos(x) ограничена на всем интервале (0, \pi) и не меняет свой знак внутри этого интервала. В результате, интеграл от этой функции на интервале (0, \pi) будет сходиться. |
Неограниченность функции на интервале интегрирования влияет на сходимость или расходимость интеграла. Если функция неограниченна на интервале, то интеграл от нее может расходиться. Если же функция ограничена на интервале, то интеграл от нее будет сходиться.
Разложение функции на сингулярные члены

Разложение функции на сингулярные члены представляет собой способ разбиения функции на более простые компоненты, называемые сингулярными членами. Этот метод позволяет исследовать поведение функции вблизи точек разрыва и определять характер ее сходимости или расходимости.
Рассмотрим функцию f(x), которая имеет точку разрыва в точке x=a. Мы можем разложить эту функцию на ряд, состоящий из сингулярных членов:
| f(x) = C_0 + C_1(x-a) + C_2(x-a)^2 + \ldots |
Здесь C_0, C_1, C_2 и так далее - коэффициенты, которые учитывают особенности поведения функции в окрестности точки разрыва. Сингулярные члены включают в себя компоненты до степени (x-a)^n, где n - целое число положительное или отрицательное.
Разложение функции на сингулярные члены особенно полезно при исследовании интегралов, которые расходятся, то есть не имеют конечного значения. С помощью этого разложения можно определить, какие компоненты функции приводят к расходимости и как их исключить или аппроксимировать, чтобы получить более точный результат.
Расходимость интеграла в несобственной точке
Проблема расходимости интеграла в несобственной точке может возникнуть в нескольких случаях. Например, если функция, которую необходимо интегрировать, имеет разрыв или особенность в данной точке, интеграл может не существовать.
Также расходимость может быть связана с производными или другими свойствами функции в несобственной точке. Например, если функция имеет бесконечное значение или растет неограниченно быстро вблизи заданной точки, интеграл может расходиться.
Расходимость интеграла в несобственной точке может иметь физическую или математическую интерпретацию. Например, в физике расходимость интеграла может означать, что соответствующая величина имеет бесконечное значение или не существует в данной точке. В математике расходимость может указывать на нарушение условий сходимости и ограниченности функции.
В общем случае, чтобы определить, расходится ли интеграл в данной несобственной точке, необходимо анализировать свойства функции и ее поведение в окрестности этой точки. Иногда можно использовать различные методы, такие как интегрирование по частям или замена переменной, чтобы справиться с расходимостью.
Конкретные примеры интегралов с расходимостью в несобственной точке могут быть сложными и требовать более глубокого математического анализа. Но понимание причин расходимости интеграла в несобственной точке является важным элементом в изучении теории интегралов и их применении в различных областях науки и техники.
Оценка интегрируемости функции
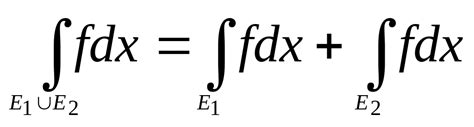
Предположим, у нас есть функция f(x), определенная на промежутке [a, b]. Чтобы оценить возможность интегрирования этой функции, мы можем построить ограничивающие площади под и над функцией на данном промежутке.
Первым шагом в оценке интегрируемости функции является разбиение промежутка [a, b] на множество малых отрезков. Затем мы находим верхние и нижние ограничивающие площади под и над каждым отрезком.
При помощи этих ограничивающих площадей мы можем оценить интеграл функции f(x) на промежутке [a, b]. Если разность между верхней и нижней ограничивающими площадями стремится к нулю при уменьшении ширины отрезков, то функция f(x) считается интегрируемой на данном промежутке.
| Отрезок | Верхняя площадь | Нижняя площадь |
|---|---|---|
| Отрезок 1 | S1 | s1 |
| Отрезок 2 | S2 | s2 |
| ... | ... | ... |
| Отрезок n | Sn | sn |
Верхняя площадь S и нижняя площадь s могут быть вычислены с использованием различных методов, например, методом прямоугольников или методом тrapezoid, а также с использованием численных методов интегрирования, таких как метод Симпсона или метод Монте-Карло.
Оценка интегрируемости функции с помощью ограничивающих площадей позволяет нам получить приближенное значение интеграла и определить, является ли функция интегрируемой на заданном промежутке.
Связь между определенными и несобственными интегралами
Определенный интеграл можно рассматривать как частный случай несобственного интеграла. Несобственный интеграл используется для рассмотрения интеграла от функций, которые не ограничены на заданном интервале или имеют особенности в пределах интегрирования. Несобственный интеграл можно рассматривать как предел значения определенного интеграла при стремлении верхнего предела интегрирования к бесконечности или при наличии особенностей на интервале.
Связь между определенными и несобственными интегралами заключается в том, что несобственный интеграл может сходиться к определенному значению, если предел его значений существует и конечен. Таким образом, сходимость несобственного интеграла означает, что определенный интеграл существует и имеет конечное значение.
В случае, если несобственный интеграл расходится, его значение не существует или бесконечно. Это говорит о том, что определенный интеграл также будет расходиться или не иметь значения на заданном интервале.
| Определенный интеграл | Несобственный интеграл |
|---|---|
| Вычисляет площадь под графиком функции на заданном интервале | Рассчитывает интеграл от функции, которая не ограничена на заданном интервале |
| Находит среднее значение функции на заданном интервале | Рассматривает интеграл от функции с особенностями в пределах интегрирования |
| Может иметь значение или расходиться | Может сходиться к значению или расходиться |
Связь между определенными и несобственными интегралами позволяет более гибко рассматривать функции с особенностями и функции, неограниченные на заданных интервалах. Это важное понимание в математическом анализе и позволяет более точно описывать и изучать различные функциональные зависимости.








