Перемножение матриц: что это такое и как работает

Перемножение матриц – это математическая операция, которая позволяет умножать одну матрицу на другую. В математике матрицы представляются в виде прямоугольных таблиц, состоящих из элементов, которые могут быть числами или другими матрицами. Перемножение матриц широко используется в различных областях, включая физику, экономику, информатику, криптографию и многие другие.

Для перемножения матриц необходимо соблюдать определенные правила. Предположим, у нас есть две матрицы – A и B. Чтобы их перемножить, мы должны умножить каждый элемент строки матрицы A на элемент столбца матрицы B и сложить полученные произведения. Результатом операции умножения будет новая матрица, размерности которой зависят от размеров исходных матриц A и B.

Пример:
Пусть у нас есть две матрицы A и B:
A = [2 4]
[1 3]
B = [5 7]
[6 8]
Для перемножения матриц A и B, мы умножим каждый элемент строки матрицы A на элемент столбца матрицы B и сложим полученные произведения:
2 * 5 + 4 * 6 = 22
1 * 5 + 3 * 6 = 17
Таким образом, результатом перемножения матриц A и B будет новая матрица C:
C = [22]
[17]

Перемножение матриц может быть сложной операцией, особенно когда матрицы имеют большой размер. Однако, это важная математическая операция, которая нашла свое применение во множестве областей и продолжает активно использоваться в современных технологиях.

Что такое матрица и зачем она нужна?

Матрицы служат для хранения и связывания данных, которые имеют структуру или связи между собой. Они могут представлять различные величины, такие как координаты, связи в сетях, значения переменных и прочее. Благодаря своей универсальности и гибкости, матрицы широко используются в различных задачах и алгоритмах.

Основной целью использования матриц является выполнение арифметических операций над элементами. С помощью матриц можно выполнять такие операции, как сложение, вычитание и умножение, а также нахождение определителя, обратной матрицы, транспонирования и т.д.

В контексте перемножения матриц, матрицы используются для представления линейных преобразований и анализа множества уравнений. Они позволяют компактно и эффективно описывать сложные системы и выполнять рассчеты с большим количеством данных.

Перемножение матриц: определение и цель

Цель перемножения матриц состоит в том, чтобы получить новую матрицу, которая является комбинацией информации из исходных матриц. Перемножение матриц широко используется в различных областях, таких как линейная алгебра, численный анализ, графический дизайн, машинное обучение и многие другие.

При перемножении матриц важно учитывать размерность исходных матриц. Для того чтобы матрицы можно было перемножить, количество столбцов в первой матрице должно быть равно количеству строк во второй матрице. Если данное условие выполняется, то результат перемножения будет матрица, у которой количество строк равно количеству строк первой матрицы, а количество столбцов равно количеству столбцов второй матрицы.

	Матрица A
Матрица B	Результат C

Как работает перемножение матриц: основные шаги алгоритма

Основные шаги алгоритма перемножения матриц:

Убедитесь, что количество столбцов первой матрицы равно количеству строк второй матрицы. Это необходимое условие для выполнения операции перемножения.
Создайте новую матрицу с размерами, равными количеству строк первой матрицы и количеству столбцов второй матрицы.
Для каждого элемента новой матрицы выполните следующие действия:
- Умножьте соответствующие элементы строки первой матрицы на соответствующие элементы столбца второй матрицы.
- Сложите полученные произведения.
Запишите полученную сумму в соответствующий элемент новой матрицы.
Повторите шаги 3-4 для всех элементов новой матрицы, пока не будет заполнена полностью.

Таким образом, в результате выполнения алгоритма перемножения матриц получается новая матрица, где каждый элемент является суммой произведений соответствующих элементов первой и второй матрицы. Этот процесс является основой для работы многих математических алгоритмов и вычислений в различных научных и технических областях.

Умножение матриц: свойства и особенности процесса

Одна из особенностей умножения матриц заключается в том, что порядок умножения имеет значение. То есть, если у нас есть матрица A размером n x m и матрица B размером m x p, то результатом их умножения будет матрица C размером n x p. Если поменять порядок матриц на B x A, результат будет отличаться.

Еще одно важное свойство умножения матриц – коммутативность. В общем случае умножение матриц не является коммутативной операцией, то есть A x B не обязательно равно B x A. Это означает, что порядок умножения имеет значение, и его не следует менять без необходимости.

Если матрицы A и B несовместимы для умножения, то умножение невозможно. Для того чтобы умножить матрицу A на матрицу B, необходимо, чтобы количество столбцов матрицы A совпадало с количеством строк матрицы B. Если это условие не выполняется, умножение матриц невозможно.

Кроме того, умножение матриц обладает свойством ассоциативности. Это значит, что при умножении трех или более матриц порядок умножения можно менять без изменения результата. Например, (A x B) x C = A x (B x C).

А	Б	В
1	2	3
4	5	6

Процесс умножения матриц может быть сложным и требует внимательности при выполнении. Правильное применение свойств и учет особенностей операции позволяют получить верный результат.

Как выбрать порядок умножения матриц

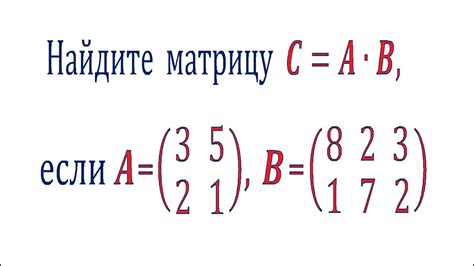
Порядок умножения матриц можно выбрать исходя из следующей формулы: если имеются матрицы A, B и C, то порядок умножения будет следующий: (A * B) * C или A * (B * C).

Порядок умножения матриц может влиять на результат и эффективность вычислений. Во многих случаях, когда порядок имеет значение, умножение матриц выполняется слева направо, то есть сначала умножают первые две матрицы, а затем полученный результат умножают на третью матрицу.

Однако, порядок умножения может быть изменен в зависимости от свойств матриц и требований задачи. Например, если матрицы являются квадратными, то порядок умножения может быть изменен с целью ускорения вычислений.

Важно отметить, что порядок умножения матриц не коммутативен, то есть результат умножения матриц A и B может отличаться от результата умножения матриц B и A. Поэтому правильный выбор порядка умножения является важным этапом при выполнении операции умножения матриц.

Матрица A	Матрица B	Матрица C
a₁₁ a₁₂ a₂₁ a₂₂	b₁₁ b₁₂ b₂₁ b₂₂	c₁₁ c₁₂ c₂₁ c₂₂

Пример:

Даны матрицы A, B и C:

A = a₁₁ a₁₂

a₂₁ a₂₂

B = b₁₁ b₁₂

b₂₁ b₂₂

C = c₁₁ c₁₂

c₂₁ c₂₂

Можно выбрать два порядка умножения: (A * B) * C и A * (B * C). Выполним умножение в обоих случаях:

(A * B) * C =

(a₁₁b₁₁ + a₁₂b₂₁)c₁₁ + (a₁₁b₁₂ + a₁₂b₂₂)c₂₁

(a₂₁b₁₁ + a₂₂b₂₁)c₁₂ + (a₂₁b₁₂ + a₂₂b₂₂)c₂₂

A * (B * C) =

a₁₁(b₁₁c₁₁ + b₁₂c₂₁) + a₁₂(b₂₁c₁₁ + b₂₂c₂₁)

a₂₁(b₁₁c₁₂ + b₁₂c₂₂) + a₂₂(b₂₁c₁₂ + b₂₂c₂₂)

Результаты умножения в обоих случаях могут быть различными, что подтверждает важность выбора правильного порядка умножения матриц.

Алгоритмы умножения матриц: обзор основных подходов

Одним из наиболее простых и распространенных алгоритмов умножения матриц является стандартный алгоритм, который основан на последовательном перемножении элементов матриц. Однако, этот алгоритм имеет время выполнения O(n^3), где n – размерность матрицы, что делает его неэффективным для больших размеров матриц.

Для оптимизации процесса умножения матриц были разработаны другие алгоритмы, которые позволяют снизить время выполнения операции. Например, алгоритм Штрассена основан на идее разделения матриц на подматрицы меньшего размера и рекурсивном умножении этих подматриц. В результате, время выполнения алгоритма Штрассена составляет O(n^log2(7)), что является значительным улучшением по сравнению со стандартным алгоритмом.

Еще одним популярным алгоритмом умножения матриц является алгоритм Фокса, который основан на идеи разбиения матриц на блоки и распределении вычислительной нагрузки между несколькими процессорами. Этот алгоритм особенно полезен при работе с параллельными системами, где можно распараллелить операцию умножения матриц для ускорения выполнения.

Кроме того, существуют и другие алгоритмы умножения матриц, такие как алгоритм Винограда, алгоритм Копперсмита-Винограда, алгоритм Густавсона и др. Каждый из этих алгоритмов имеет свои особенности и применимость в зависимости от конкретной задачи.

В итоге, выбор оптимального алгоритма умножения матриц зависит от размерности матриц, доступных ресурсов и требуемой производительности. При выборе алгоритма следует учитывать все эти факторы для достижения наилучшего результата.

Какие задачи можно решить с помощью умножения матриц

Одной из основных задач, которую можно решить с помощью умножения матриц, является решение систем линейных уравнений. Задачи нахождения решений векторных уравнений, определение коэффициентов векторов-столбцов и нахождение обратной матрицы могут быть решены с использованием умножения матриц.

Умножение матриц также применяется в компьютерной графике для преобразования трехмерных точек и объектов. Матрицы преобразования используются для поворота, масштабирования и сдвига объектов на экране.

В экономике и финансах умножение матриц широко используется для моделирования и анализа финансовых данных. Оно позволяет определить взаимосвязь и зависимость между различными переменными, а также предсказывать будущие значения.

Умножение матриц находит свое применение в машинном обучении и искусственном интеллекте. Матрицы используются для хранения и представления данных, а также для вычисления весов и параметров моделей. Алгоритмы обучения машинного обучения, такие как градиентный спуск и метод наименьших квадратов, основаны на операциях умножения матриц.

Основываясь на этом, можно сделать вывод, что умножение матриц является мощным инструментом для решения различных задач в различных областях математики и ее приложений.

Реализация перемножения матриц на практике: примеры кода

Пример на Python:


def matrix_multiply(a, b):
rows_a = len(a)
cols_a = len(a[0])
rows_b = len(b)
cols_b = len(b[0])
if cols_a != rows_b:
return None
result = [[0 for _ in range(cols_b)] for _ in range(rows_a)]
for i in range(rows_a):
for j in range(cols_b):
for k in range(cols_a):
result[i][j] += a[i][k] * b[k][j]
return result
# Пример использования функции
matrix_a = [[1, 2, 3], [4, 5, 6]]
matrix_b = [[7, 8], [9, 10], [11, 12]]
result = matrix_multiply(matrix_a, matrix_b)
print(result)

Пример на JavaScript:


function matrixMultiply(a, b) {
const rows_a = a.length;
const cols_a = a[0].length;
const rows_b = b.length;
const cols_b = b[0].length;
if (cols_a !== rows_b) {
return null;
}
const result = new Array(rows_a).fill(0).map(() => new Array(cols_b).fill(0));
for (let i = 0; i

В этих примерах функции matrix_multiply (на Python) и matrixMultiply (на JavaScript) принимают две матрицы в виде двумерных массивов и возвращают результат перемножения матриц в виде новой матрицы. Также в коде присутствует проверка размерностей матриц и возвращение null (Python) или null (JavaScript), если матрицы невозможно перемножить.

Обратите внимание, что в обоих примерах используется вложенный цикл для перемножения элементов матриц. Внешние циклы перебирают строки первой матрицы, внутренний цикл перебирает столбцы второй матрицы, а вложенный цикл внутри них вычисляет значение каждого элемента результирующей матрицы.

Перемножение матриц: определение и применение