Перечисление свойств графика функций является важным инструментом для анализа и исследования математических функций. Оно предоставляет возможность визуально представить зависимость переменных и проявления функции на плоскости. Перечисление свойств графика функций позволяет понять и оценить такие параметры, как область определения функции, область значений, поведение функции на разных участках, а также присутствие асимптот и экстремумов.
Перечисление свойств графика функций также является важным шагом в изучении и понимании математических функций. Благодаря анализу и визуализации графика можно определить особые точки, разрывы, периодичность и симметрию функции. Это позволяет провести качественный анализ функции без использования сложных вычислений и доказательств, а также дает представление об их глобальном поведении.
Перечисление свойств графика функций также имеет практическую значимость. Оно позволяет определить области, где функция монотонно возрастает или убывает, а также найти экстремумы. Это может быть полезно при моделировании процессов, определении границ допустимых значений и оптимизации в различных областях науки и техники. При помощи перечисления свойств графика функций можно строить зависимости, оптимизировать параметры и прогнозировать результаты.
Понятие графика функций
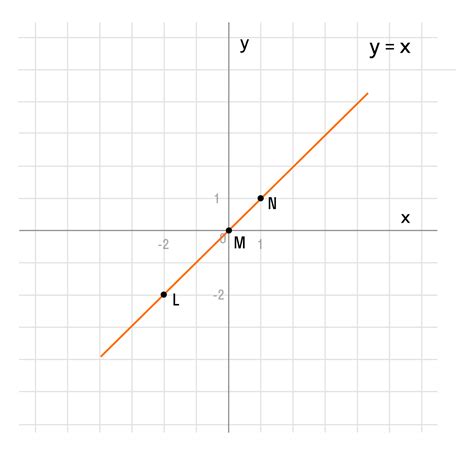
График функций состоит из точек, представляющих значения функции при различных значениях аргумента. Для построения графика обычно выбирается прямоугольная система координат, где аргумент откладывается по горизонтальной оси (ось абсцисс), а значение функции откладывается по вертикальной оси (ось ординат).
График функции может иметь различные формы и свойства. На графике можно определить, есть ли у функции точка перегиба, участки возрастания и убывания, локальные и глобальные экстремумы, асимптоты и другие характеристики.
Построение графика функции является важным инструментом в изучении математики и научных дисциплин. С помощью графика можно визуально представить и понять сложные математические концепции, а также анализировать и сравнивать различные функции.
Для более точного исследования графика функции можно использовать методы математического анализа и геометрии. Это позволяет более детально изучить свойства функции и получить более точные выводы о ее поведении.
| Символ | Описание |
|---|---|
| Р | Аргумент |
| У | Значение функции |
| (Р, У) | Точка на графике |
Определение и основные характеристики
Одной из основных характеристик графика функции является его видимость. График может быть видимым на всей области определения функции или только на определенной части. Также, график может быть непрерывным или иметь разрывы.
Определение основных характеристик графика функции также включает определение экстремальных точек. Экстремальные точки - это точки на графике функции, которые являются максимальными или минимальными значениями функции.
Другой характеристикой графика функции является его поведение вблизи асимптот. График может стремиться к определенным прямым или кривым, которые называются асимптотами. Асимптоты могут быть горизонтальными, вертикальными или наклонными.
Также, график функции может иметь точки перегиба. Точки перегиба - это точки, в которых меняется направление изгиба графика функции. Они могут быть локальными минимумами или максимумами функции.
Наконец, перечисление свойств графика функций включает определение интервалов возрастания и убывания. Интервалы возрастания - это промежутки на которых значения функции увеличиваются. Интервалы убывания - это промежутки на которых значения функции уменьшаются.
Все эти основные характеристики позволяют получить представление о различных аспектах графика функции и использовать их для дальнейшего анализа и решения уравнений.
Важность выбора подходящей функции для графика
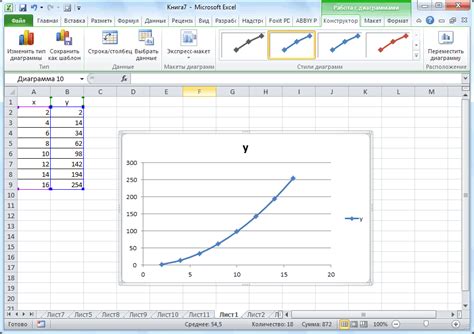
Одним из основных критериев выбора функции является учет формы графика и особенностей изучаемых данных или явления. Например, если требуется изучить экспоненциальную зависимость, то подходящей функцией будет экспоненциальная функция.
Также важно учитывать, что различные функции могут иметь различные участки графика, такие как экстремумы, разрывы или асимптоты. Правильный выбор функции позволяет точнее описать и визуализировать такие особенности.
Кроме того, выбор подходящей функции упрощает вычисление значений функции и анализ ее свойств. Например, если требуется найти точку перегиба или асимптоту, то с помощью соответствующей функции это может быть сделано более эффективно.
Таким образом, выбор подходящей функции является важным этапом в построении графика функции, позволяющим более полно и точно описать изучаемое явление и провести его анализ.
Типы функций и их влияние на график
При построении графика функций, тип функции играет важную роль. Тип функции определяет ее свойства и поведение, а также влияет на форму и характер графика. В данном разделе мы рассмотрим основные типы функций и их влияние на график.
1. Линейные функции. Линейная функция представляет собой прямую линию на графике. Ее уравнение имеет вид y = kx + b, где k - коэффициент наклона, b - свободный член. Линейные функции имеют постоянный коэффициент наклона и создают прямые линии с различным углом наклона.
2. Квадратичные функции. Квадратичная функция имеет вид y = ax^2 + bx + c, где a, b, c - коэффициенты. График квадратичной функции представляет собой параболу. В зависимости от значения коэффициента a парабола может быть направлена вверх (a > 0) или вниз (a
3. Степенные функции. Степенная функция имеет вид y = ax^n, где a - коэффициент, n - показатель степени. График степенной функции может иметь различные формы в зависимости от значения показателя степени. Например, при n > 1 график будет возрастающей кривой, при 0
4. Тригонометрические функции. Тригонометрические функции (синус, косинус, тангенс и др.) имеют периодические графики. Графики этих функций представляют собой повторяющиеся колебания в зависимости от аргумента.
5. Экспоненциальные функции. Экспоненциальная функция имеет вид y = a*b^x, где a, b - коэффициенты. График экспоненциальной функции характеризуется быстрым ростом или спадом в зависимости от знака коэффициента b.
6. Логарифмические функции. Логарифмическая функция имеет вид y = log_a x, где a - основание логарифма. График логарифмической функции имеет форму гиперболы и ограничен ветвями.
Различные типы функций создают разнообразные формы графиков с уникальными свойствами. Понимание этих свойств позволяет анализировать и интерпретировать графики функций, а также использовать их для решения математических задач.
Роль основных свойств графика функций
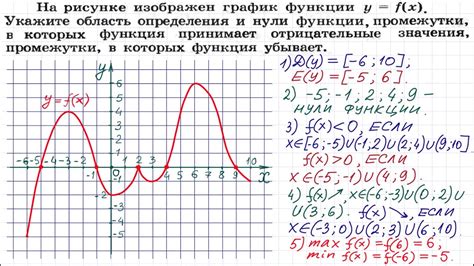
Основные свойства графика функции предоставляют информацию о его форме, поведении и характеристиках функции. Рассмотрим некоторые из этих свойств:
| Свойство | Описание |
|---|---|
| Монотонность | Указывает на изменение знака производной функции на определенном интервале. Свойство монотонности позволяет определить, является ли функция возрастающей или убывающей. |
| Экстремумы | Показывает точки, в которых функция достигает локального минимума или максимума. Экстремумы могут быть как точечными, так и локальными. |
| Асимптоты | Описывают поведение функции в бесконечности. Асимптоты могут быть горизонтальными, вертикальными или наклонными. |
| Периодичность | Позволяет установить, имеет ли функция периодическое повторение своих значений. Если функция периодическая, то ее график будет иметь повторяющиеся участки. |
| Амплитуда | Определяет максимальное отклонение функции от основной линии графика. Амплитуда может быть положительной или отрицательной. |
Знание и понимание основных свойств графика функции позволяет анализировать и интерпретировать ее поведение, а также делать выводы о ее особенностях. Например, знание свойства монотонности позволяет определить интервалы, на которых функция возрастает или убывает, что может быть полезным при решении задач оптимизации или нахождении экстремумов.
Аргумент и область определения
Область определения функции - это множество значений аргумента, при которых функция определена. В графике функции это может быть участок числовой прямой или плоскости, где функция имеет смысл.
Область определения можно представить в виде таблицы, где указывается значение аргумента и соответствующее значение функции. Например:
| Аргумент (x) | Значение функции (y) |
|---|---|
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
Из данной таблицы можно понять, что область определения функции y = x^2 является множеством всех действительных чисел.
Значение точек и линий на графике

При построении графика функции, точки и линии играют важную роль, помогая визуально представить различные характеристики функции. Они помогают наглядно продемонстрировать различные аспекты функции, такие как экстремумы, перегибы, нули функции и другие важные особенности.
Точки на графике функции отображают значения функции для различных значений аргумента. Они помогают определить значения функции в определенных точках, а также легко определить экстремумы функции. Например, вершина параболы, где кривая функции достигает максимального или минимального значения, будет представлена точкой на графике.
Линии на графике, в свою очередь, помогают визуализировать связь между различными точками на графике, а также позволяют определить форму функции. Например, прямая линия на графике может указывать на линейную зависимость между переменными. Склонность линии может указывать на угол наклона и тем самым давать представление о том, как меняется функция в зависимости от значения аргумента.
Комбинация точек и линий на графике функции позволяет легко интерпретировать различные характеристики функции и делать выводы о ее поведении в разных точках. Наличие особых точек и линий на графике может указывать на наличие экстремумов, перегибов, асимптот и других важных особенностей функции.
Таким образом, точки и линии на графике функции имеют большое значение, помогая наглядно представить характеристики функции и легко интерпретировать ее поведение. Это особенно полезно при анализе функций и решении различных математических задач.
То, что можно понять из графика функции
Первый взгляд на график может дать представление о свойствах функции. Если график возрастает слева направо, то функция возрастает. Если график убывает слева направо, то функция убывает. При этом, если график растет или убывает все время, то функция называется монотонной. Если отсутствуют участки возрастания или убывания, то функция называется немонотонной.
Нули функции – это точки на графике, в которых значение функции равно нулю. Нули функции являются корнями уравнения f(x) = 0 и позволяют найти решения уравнения. Нули функции можно определить на графике, где функция пересекает ось абсцисс.
Экстремумы функции – это точки локального минимума и максимума функции. Локальный минимум – это точка, в которой функция принимает наименьшее значение в некоторой окрестности. Локальный максимум – это точка, в которой функция принимает наибольшее значение в некоторой окрестности. Экстремумы функции можно определить на графике, где функция имеет "пики" или "ямки".
Асимптоты функции – это прямые или кривые, которым график функции стремится при приближении к бесконечности или в бесконечности. График функции может иметь горизонтальную, вертикальную или наклонную асимптоту. Асимптоты функции позволяют понять ограничения поведения функции на бесконечности и используются, например, при нахождении предела функции.
Интервалы возрастания и убывания – это участки на графике, на которых функция возрастает или убывает. Интервалы возрастания определяются теми участками, где график функции поднимается вверх, а интервалы убывания – теми участками, где график функции опускается вниз. Знание интервалов возрастания и убывания функции позволяет понять ее поведение и локализовать экстремумы.
Изучение графика функции позволяет получить множество полезной информации о свойствах функции. Путем анализа графика можно определить монотонность функции, нули функции, экстремумы, асимптоты, а также интервалы возрастания и убывания. Вместе с другими методами анализа функций, анализ графика является важным инструментом математического исследования функций и помогает строить более точные представления о самой функции.
Влияние параметров на форму графика функции

При построении графика функции важно учитывать влияние ее параметров на его форму. Параметры функции могут включать такие характеристики, как коэффициенты, степени или корни.
Один из основных параметров, влияющих на график функции, - это коэффициенты при переменных. Изменение коэффициентов приводит к изменению угла наклона графика и его масштаба. Например, при увеличении коэффициента при переменной увеличивается наклон графика. Также можно изменять коэффициенты для сдвига графика функции вверх или вниз, вправо или влево.
Еще одним важным параметром графика функции является степень. Изменение степени переменных может привести к изменению форму графика. Например, при увеличении степени переменной, график становится более «крутым», а при уменьшении степени - менее «крутым».
Корни - еще один важный параметр, который влияет на форму графика функции. Если функция имеет корни, они определяют точки пересечения графика с осью x. Корни функции могут быть различной кратности, что также влияет на форму графика.
При построении графика функции необходимо учитывать все параметры, так как они существенно влияют на его форму и позволяют более точно представить поведение функции.








