Ортоцентр – это одна из важных точек внутри треугольника, которая связана с его высотами. Он является пересечением высот треугольника и обладает рядом удивительных геометрических свойств.
Для определения ортоцентра треугольника необходимо провести высоты из каждой вершины, то есть прямые, перпендикулярные сторонам треугольника и проходящие через противоположные вершины. Их пересечение и будет ортоцентром.
Главное свойство ортоцентра состоит в том, что он лежит на всех трех высотах треугольника. Это означает, что сумма расстояний от ортоцентра до каждой из вершин треугольника равна нулю.
Кроме того, ортоцентр является точкой пересечения описанных окружностей треугольника, образованных с основаниями высот. Он также является центром прямоугольного треугольника, образованного со сторонами, равными высотам треугольника.
Ортоцентр треугольника – это ключевая точка, которая не только имеет важные геометрические свойства, но и является важным инструментом в решении задач треугольниковой геометрии.
Что такое ортоцентр треугольника?
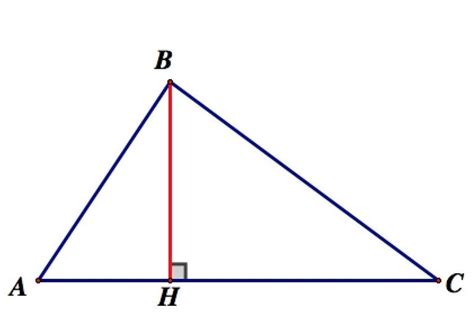
Ортоцентр является одной из особых точек треугольника и обозначается буквой H.
Свойства ортоцентра треугольника:
- Ортоцентр треугольника может быть внутренней точкой треугольника, если все его углы острые.
- Ортоцентр также может быть точкой на стороне треугольника, если один из его углов тупой.
- Если треугольник является равнобедренным, ортоцентр будет лежать на середине основания.
- Если треугольник является прямоугольным, то ортоцентр совпадает с вершиной прямого угла.
Ортоцентр треугольника имеет важное значение при решении геометрических задач и играет роль при определении других особых точек треугольника, таких как центр описанной окружности и точки Ферма.
Связь ортоцентра с высотами треугольника
1. Ортоцентр лежит на всех трех высотах треугольника. Это означает, что отрезки, соединяющие ортоцентр с серединами сторон треугольника, являются высотами.
2. Расстояние от ортоцентра до любой стороны треугольника равно длине соответствующей высоты. Это означает, что ортоцентр является ортогональной проекцией вершины треугольника на соответствующую сторону.
3. Ортоцентр является центром вписанной окружности, описанной окружности и окружности Эйлера треугольника.
4. Ортоцентр является точкой пересечения трех радикальных осей треугольника - прямых, соединяющих вершины треугольника с ортоцентром и перпендикулярных соответствующим высотам.
Таким образом, ортоцентр треугольника тесно связан с высотами треугольника и обладает множеством интересных свойств, которые используются при решении различных геометрических задач.
Теорема о расположении ортоцентра в прямоугольном треугольнике
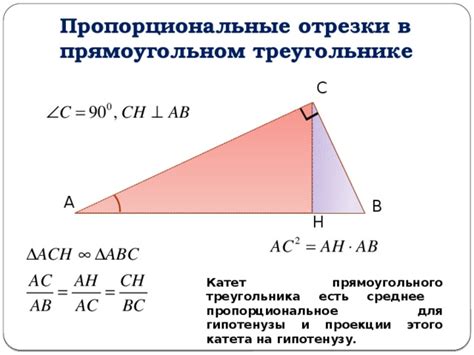
Таким образом, в прямоугольном треугольнике ортоцентр находится на вершине с прямым углом и является точкой пересечения высот.
Высоты прямоугольного треугольника можно легко найти, используя его стороны. Высота, проведенная из вершины с прямым углом, будет равна половине гипотенузы треугольника. Высоты, проведенные из вершин катетов, будут равны соответствующим катетам.
Также отметим, что в прямоугольном треугольнике, ортоцентр совпадает с точкой пересечения медиан и центром окружности, описанной вокруг треугольника.
Ортоцентр прямоугольного треугольника является ключевой точкой для решения различных геометрических задач и имеет множество интересных свойств, которые могут быть использованы для решения задач на практике.
Система координат в ортоцентре треугольника
Система координат, связанная с ортоцентром треугольника, называется ортоцентрической системой координат. В этой системе, вершины треугольника обозначаются буквами A, B и C, а ортоцентр – буквой H.
В ортоцентрической системе координат середины сторон треугольника обозначаются буквами D, E и F. Координаты вершин и ортоцентра могут быть представлены как пары чисел (x, y), где x – расстояние от ортоцентра до прямой, содержащей одну из сторон треугольника, а y – расстояние от ортоцентра до прямой, содержащей другую сторону треугольника.
Ортоцентрическая система координат позволяет анализировать треугольник с точки зрения его геометрических свойств и отношений между его элементами. Также она может быть полезной при решении задач, связанных с треугольником или его свойствами.
Симметричное отражение относительно ортоцентра

Симметричное отражение относительно ортоцентра - это геометрическое преобразование, при котором каждая точка трансформируется в ее симметричную относительно ортоцентра.
Симметричное отражение относительно ортоцентра обладает следующими свойствами:
- Точки, лежащие на сторонах треугольника и трех его высотах, при симметричном отражении остаются на своем месте.
- Симметричное отражение относительно ортоцентра обладает свойством инвариантности длин отрезков и углов между ними.
- Симметричное отражение относительно ортоцентра является обратимым преобразованием, то есть повторное применение этого преобразования к исходному треугольнику приведет к его исходному положению.
Симметричное отражение относительно ортоцентра является одним из фундаментальных преобразований в геометрии треугольников и находит применение в решении задач о построении или анализе свойств треугольников.
Связь ортоцентра с описанной окружностью треугольника
Описанной окружностью треугольника называется окружность, проходящая через все вершины треугольника. Она имеет свои особенности и связана с ортоцентром треугольника, точкой пересечения его высот.
Одним из свойств ортоцентра треугольника является то, что он лежит на описанной окружности треугольника. Для каждого треугольника ортоцентр лежит на описанной окружности, однако это не обязательно означает, что ортоцентр является центром этой окружности.
Существует также обратное утверждение: если точка лежит на описанной окружности треугольника, то она является ортоцентром этого треугольника. Таким образом, ортоцентр треугольника может быть найден как пересечение высот треугольника, но также может быть найден и как пересечение прямых, проходящих через вершину треугольника и середину противолежащей стороны.
Связь ортоцентра с описанной окружностью треугольника играет важную роль в геометрии. Она позволяет решать различные задачи, связанные с треугольниками, например, находить различные углы и расстояния в треугольнике, определять центры окружностей, вписанных в треугольник, и т. д.
| Схематическое изображение ортоцентра треугольника и его связи с описанной окружностью |
 |
На схеме изображена связь ортоцентра треугольника ABC (точка H) с описанной окружностью треугольника (окружность с центром O). Видно, что ортоцентр H лежит на описанной окружности, но не является ее центром.
Из данной связи следует, что если мы знаем радиус и центр описанной окружности треугольника, то можем определить ортоцентр треугольника и наоборот - если мы знаем ортоцентр треугольника, можем найти радиус и центр его описанной окружности.
Таким образом, связь ортоцентра с описанной окружностью треугольника позволяет получать важную информацию о треугольнике и упрощает решение геометрических задач, связанных с треугольниками.
Связь ортоцентра с описанной окружностью в прямоугольном треугольнике
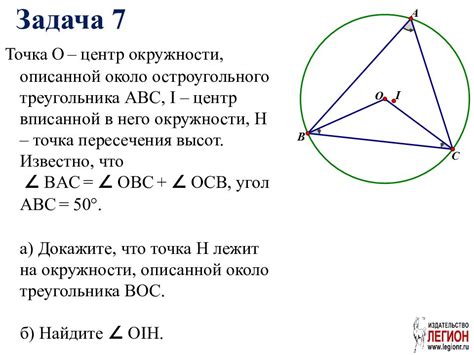
Описанная окружность в прямоугольном треугольнике проходит через все вершины треугольника и имеет диаметр, совпадающий с гипотенузой треугольника. Связь между ортоцентром и описанной окружностью заключается в том, что ортоцентр треугольника является серединой отрезка, соединяющего вершину прямого угла и центр описанной окружности.
Это свойство можно доказать следующим образом: так как ортоцентр треугольника является пересечением высот, он располагается на пересечении перпендикуляров к сторонам треугольника, проведенных через их середины. Пусть точка H обозначает ортоцентр, точка O - центр описанной окружности, и А, В, С - вершины треугольника. Так как вершина прямого угла лежит на окружности, то полусумма углов треугольника, образованных прямым углом и двумя сторонами, равна 180 градусов. Значит, углы AHС и AOC являются смежными и равными между собой углами, а также являются прямыми углами, так как основание прямого угла лежит на окружности. Отсюда следует, что треугольник АОС равнобедренный, и отрезок AH является медианой треугольника АОС и равен радиусу описанной окружности.
Отметим также, что в прямоугольном треугольнике ортоцентр совпадает с пересечением биссектрис треугольника, проведенных через его вершины. Данное свойство можно использовать для определения ортоцентра, если известны координаты вершин треугольника или известны уравнения прямых, на которых лежат его стороны.








