В математике понятие ограниченности функции является важным для понимания ее поведения и свойств. Функция называется ограниченной сверху, если для всех значений аргумента функции найдется такое число, которое будет больше или равно значению функции. И наоборот, функция считается ограниченной снизу, если для всех значений аргумента функции найдется такое число, которое будет меньше или равно значению функции.
В контексте графика функции, ограниченность сверху означает, что график функции лежит ниже некоторой горизонтальной прямой. Другими словами, нет значения функции, которое было бы больше всех остальных значений. Аналогично, ограниченность снизу означает, что график функции лежит выше некоторой горизонтальной прямой. Нет значения функции, которое было бы меньше всех остальных значений.
Ограниченность функции может быть полезной для множества практических задач. Например, в экономике, ограниченность сверху может указывать на максимальное количество товара, которое может быть произведено или продано в определенном периоде времени. Ограниченность снизу может указывать на минимальную стоимость товара, которая может быть установлена для его продажи.
Важно отметить, что ограниченность функции не означает, что ее значения находятся внутри интервала между ограничивающими прямыми. Ограниченная функция может иметь значения, которые находятся как ниже, так и выше этих прямых. Главное, чтобы существовали ограничения сверху или снизу.
Функция ограничена сверху или снизу: понятие и примеры
Когда говорят, что функция ограничена сверху или снизу, имеется в виду, что существует некоторое число, которым все значения функции ограничены.
Функция ограничена сверху, если существует число, называемое верхней границей, такое, что все значения функции меньше или равны этой верхней границе. В математической нотации это записывается как:
f(x) ≤ M, для всех х из области определения функции, где М - верхняя граница.
Например, функция f(x) = x^2 ограничена сверху, так как для любого значения x в области определения функции, значение f(x) будет меньше или равно числу M=1.
Функция ограничена снизу, если существует число, называемое нижней границей, такое, что все значения функции больше или равны этой нижней границе. В математической нотации это записывается как:
f(x) ≥ m, для всех х из области определения функции, где m - нижняя граница.
Например, функция f(x) = sin(x) ограничена снизу, так как для любого значения x в области определения функции, значение f(x) будет больше или равно числу m=-1.
Определение функции ограниченной сверху
Функция называется ограниченной сверху на интервале, если существует некоторое число, называемое верхней границей, такое что все значения функции на этом интервале не превышают заданное число.
Математически это можно записать следующим образом:
Дана функция f(x), определенная на интервале (a, b). Если существует число M, такое что для любого x из интервала выполняется неравенство f(x) ≤ M, то функция f(x) ограничена сверху на интервале (a, b).
Число M называется верхней границей функции f(x) на интервале (a, b).
Иногда вместо "ограничена сверху" говорят "ограничена сверху на интервале" или "имеет верхнюю границу на интервале".
Концы интервала, то есть значения a и b, могут быть как конечными, так и бесконечными.
Как определить ограниченность функции сверху числом
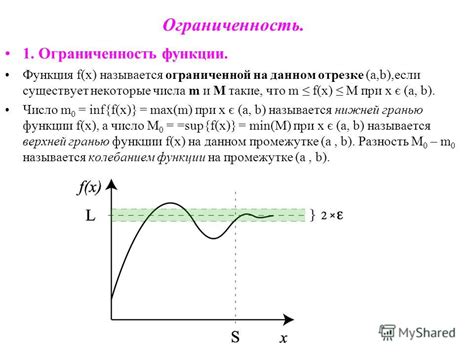
Ограниченность функции сверху числом означает, что функция на всей своей области определения не превосходит этого числа. То есть, существует такое число M, что для любого значения x из области определения функции f(x), значение f(x) будет меньше или равно M.
Для определения ограниченности функции сверху числом можно использовать различные методы. Один из них - аналитический метод. Для этого необходимо найти производную функции и исследовать её поведение в пределах области определения.
Если производная функции положительна на всей области определения, это означает, что функция возрастает и не имеет верхней грани. Если производная функции отрицательна на всей области определения, это означает, что функция убывает и не имеет верхней грани. В этих случаях функция не ограничена сверху.
Если производная функции меняет знак, то необходимо найти точки экстремума - места, где производная равна нулю или не определена. Определив значение функции в этих точках, можно сделать вывод о её ограниченности или неограниченности сверху.
Другим методом определения ограниченности функции сверху числом является графический метод. Для этого необходимо построить график функции и найти его высшую точку. Если эта точка не имеет верхней точки, то функция ограничена сверху. Если график функции стремится к бесконечности сверху, то функция не ограничена сверху.
Таким образом, определение ограниченности функции сверху числом требует анализа поведения функции на всей области определения и может быть проведено как аналитическим, так и графическим методом.
Понятие функции ограниченной снизу
Функция ограничена снизу, если существует такое число $M$, что для всех значений $x$ из области определения функции выполнено неравенство $f(x) \geq M$. Иными словами, снизу ограниченная функция имеет нижнюю границу, которая не превосходит все значения функции.
Чтобы проиллюстрировать понятие функции ограниченной снизу, рассмотрим следующую таблицу:
| $x$ | $f(x)$ |
|---|---|
| 1 | 2 |
| 2 | 5 |
| 3 | 7 |
| 4 | 3 |
В данном случае функция $f(x)$ ограничена снизу значением $M = 2$, так как для всех значений $x$ из области определения функции выполняется неравенство $f(x) \geq 2$. Минимальное значение функции равно 2, и оно не превосходит все значения функции.
Ограниченность функции снизу имеет важное значение при изучении свойств функций и их графиков. Она помогает определить нижнюю границу для значений функции и установить, насколько функция может быть близка к этой границе.
Примеры функций, ограниченных сверху
Вот несколько примеров функций, ограниченных сверху:
1. Функция синуса: $f(x) = \sin(x)$ для всех $x \in \mathbb{R}$. Эта функция ограничена сверху числом 1, так как $|\sin(x)| \leq 1$ для всех значений $x$.
2. Функция экспоненты: $f(x) = e^x$ для всех $x \in \mathbb{R}$. Эта функция ограничена сверху любым положительным числом, так как $e^x$ стремится к бесконечности при $x \to +\infty$.
3. Линейная функция: $f(x) = mx + b$ для всех $x \in \mathbb{R}$, где $m$ - наклон, а $b$ - точка пересечения с осью ординат. Если $m > 0$, то функция ограничена сверху. Например, функция $f(x) = 2x + 3$ ограничена сверху числом 9.
Замечание: Функция может быть ограничена сверху, но не иметь максимального значения. Например, фунция $f(x) = \frac{1}{x}$ для всех $x \in (0, +\infty)$ ограничена сверху числом 1, но не достигает этой верхней границы.
Примеры функций, ограниченных снизу
Ниже приведены несколько примеров функций, которые ограничены снизу:
- Функция синуса: Функция синуса (sin(x)) является периодической и график её колеблется между -1 и 1 на всей числовой оси. Следовательно, она ограничена снизу значением -1.
- Функция квадратного корня: Функция квадратного корня (sqrt(x)) ограничена снизу значением 0, так как квадратный корень из любого неотрицательного числа равен или больше 0.
- Функция экспоненты: Функция экспоненты (exp(x)) всегда больше 0 на всей числовой оси, поэтому она ограничена снизу значением 0.
Это лишь некоторые примеры функций, ограниченных снизу. В математике существует много других функций, которые также могут иметь нижнюю границу, их анализ и изучение является объектом специальных разделов математики.
Функция ограничена сверху и снизу: определение и примеры
Пусть дана функция f(x), определенная на интервале [a, b].
Функция f(x) будет ограничена сверху, если существует число M, такое что для всех x из указанного интервала выполняется неравенство f(x) ≤ M.
Функция f(x) будет ограничена снизу, если существует число m, такое что для всех x из указанного интервала выполняется неравенство f(x) ≥ m.
Для лучшего понимания понятия ограниченности функции сверху и снизу, рассмотрим примеры:
- Пусть функция f(x) = x^2 определена на интервале [-2, 2]. В данном случае функция будет ограничена снизу числом 0, так как для всех x из указанного интервала выполняется неравенство f(x) ≥ 0. Однако функция не будет ограничена сверху, так как для любого числа M существует такое x, что f(x) > M.
- Рассмотрим функцию f(x) = sin(x), определенную на интервале [0, π]. В данном случае функция ограничена сверху числом 1, так как для всех x из указанного интервала выполняется неравенство f(x) ≤ 1. Также функция будет ограничена снизу числом -1, так как для всех x из указанного интервала выполняется неравенство f(x) ≥ -1.
- Пусть дана функция f(x) = e^x, определенная на интервале (-∞, ∞). В данном случае функция ограничена снизу числом 0, так как для всех x из указанного интервала выполняется неравенство f(x) ≥ 0. Однако функция не будет ограничена сверху, так как для любого числа M существует такое x, что f(x) > M.
Таким образом, ограниченность функции сверху и снизу - это свойство функции, позволяющее определить, существуют ли верхние и нижние границы значений функции на заданном интервале.
Как определить ограниченность функции на интервале
Функция считается ограниченной сверху на определенном интервале, если для любого значения x из этого интервала существует такое число M, что значение функции f(x) остается меньше или равным M. То есть, существует такое число M, что f(x) ≤ M для всех x на интервале.
Аналогично, функция считается ограниченной снизу на интервале, если для любого значения x из этого интервала существует такое число L, что значение функции f(x) остается больше или равным L. То есть, существует такое число L, что f(x) ≥ L для всех x на интервале.
Для определения ограниченности функции на интервале необходимо определить, существуют ли такие числа M и L, для которых выполняются условия, указанные выше. Для этого можно проанализировать поведение функции на интервале, вычислить максимальное и минимальное значение функции на этом интервале или построить график функции и изучить его свойства.
Если удалось найти такие числа M и L, то функция считается ограниченной на интервале. В противном случае функция считается неограниченной на этом интервале.
Интерпретация ограниченности функции в контексте графика
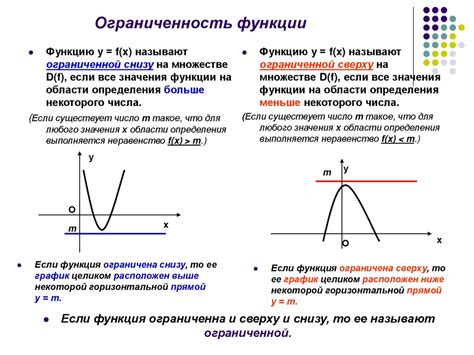
Ограниченность функции сверху или снизу может быть интерпретирована в контексте графика функции.
Если функция ограничена сверху, это означает, что существует горизонтальная прямая, которая является верхней границей для графика функции. То есть ни одна точка графика функции не лежит выше этой прямой. Визуально, график функции находится полностью под данной горизонтальной прямой.
Если же функция ограничена снизу, то существует горизонтальная прямая, которая является нижней границей для графика функции. То есть ни одна точка графика функции не лежит ниже этой прямой. График функции находится полностью над данной горизонтальной прямой.
Если функция ограничена и сверху, и снизу, то существуют две горизонтальные прямые, обрамляющие график функции. Визуально, точки графика функции находятся между этими двумя прямыми.
Ограниченность функции сверху или снизу имеет важное значение в различных математических и физических контекстах. Например, при изучении пределов функций или определенных интегралов, знание ограниченности функции помогает в анализе и вычислениях.
Значение функций ограничения для анализа функций
Аналогично, когда функция ограничена снизу, это означает, что существует число, которое является нижней границей для всех значений функции. Функция не может быть меньше этого числа.
Знание функций ограничения позволяет анализировать и понимать поведение функций и их значимости. Если функция ограничена сверху, это может говорить о том, что функция имеет максимальное значение и не может быть больше этого значения. Аналогично, если функция ограничена снизу, это может говорить о том, что функция имеет минимальное значение и не может быть меньше этого значения.
Ограничения функций также могут быть полезны для определения границы роста или убывания функции. Например, если функция ограничена сверху, то это может говорить о том, что функция растет до определенного максимального значения, после которого она остается постоянной или начинает убывать.
Важно отметить, что ограничения функций могут быть как конкретными числами, так и выражениями. Например, функция может быть ограничена числом 10 или выражением типа x + 5. Эти ограничения могут меняться в зависимости от контекста и требований анализа функции.
Таким образом, понимание и использование функций ограничения позволяет более глубоко исследовать и анализировать функции, их поведение и свойства. Это важный инструмент в математике и науке, который позволяет более точно определить характер и значение функций.








