Неравенства – неотъемлемая часть математического анализа, их решение позволяет определить множество значений, для которых неравенство истинно. При этом, одной из важных задач является нахождение всех целочисленных решений неравенства. Целые решения позволяют нам получить конкретные числовые значения, удовлетворяющие неравенству, и часто находят применение в реальных задачах.
Под понятием "целочисленные решения" понимаются такие значения переменных, при подстановке которых в неравенство, оно остается верным. Например, для неравенства 2x + 3 > 5, целочисленным решением будет любое значение x, для которого 2x + 3 больше 5. Если рассматривать только целые значения переменной x, то все решения можно получить путем перебора всех целых чисел и проверки их на соответствие неравенству.
Однако, существуют разные подходы к решению неравенств. Например, в случае линейных неравенств можно использовать графический метод или алгоритмы решения систем линейных неравенств. В случае квадратных и иных нелинейных неравенств, достаточно сложно получить все целочисленные решения на основе перебора. Для этого обычно применяются методы математической логики и алгебры.
В общем случае, для нахождения всех целых решений неравенств, необходимо применять специальные методы и алгоритмы, которые зависят от типа неравенства и его сложности. Это может включать применение системы диофантовых уравнений, методов численного анализа, алгоритмов поиска корней уравнений и других математических методов.
История и примеры неравенств
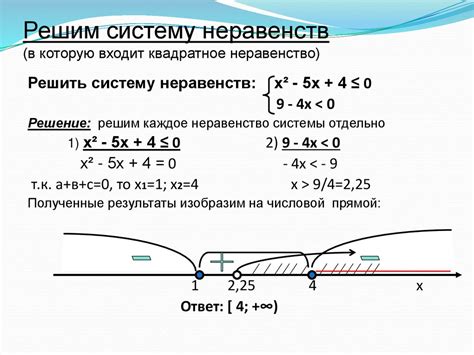
Одним из классических примеров неравенств является неравенство между средними арифметическим и геометрическим значениями для положительных чисел. Для двух чисел a и b, среднее арифметическое (S) равно (a + b) / 2, а среднее геометрическое (G) равно sqrt(a * b).
Тогда неравенство средних утверждает, что S >= G, что можно записать в виде (a + b) / 2 >= sqrt(a * b). Это неравенство имеет простое геометрическое истолкование: среднее арифметическое двух чисел всегда больше или равно среднему геометрическому этих чисел.
Другой пример неравенства, которое обычно изучается в школе, - это неравенство между абсолютными значениями. Для любого числа x, его абсолютное значение (|x|) равно расстоянию между x и нулем на числовой оси.
Таким образом, |x| >= 0 всегда, поскольку расстояние между числом и нулем не может быть отрицательным. Это неравенство также имеет простое геометрическое истолкование: абсолютное значение любого числа всегда больше или равно нулю.
| Примеры неравенств | Решение |
|---|---|
| x + 5 > 10 | x > 5 |
| 2y | y |
| 3z + 7 >= 22 | z >= 5 |
В таблице приведены примеры неравенств и их решения. Для решения неравенств, нужно определить все значения переменной, которые удовлетворяют неравенству. Если неравенство содержит знак > или = или
При решении неравенств, важно помнить правила замены и операций сравнения. Например, при умножении или делении обоих частей неравенства на отрицательное число, знак неравенства изменяется на противоположный.
В заключение, неравенства широко применяются в различных областях, включая алгебру, геометрию, теорию вероятности и теорию игр. Изучение неравенств помогает развить логическое мышление и умение решать сложные математические задачи.
Определение целого решения неравенства
Для того чтобы найти все целые решения неравенства, необходимо следовать определенным шагам:
- Переформулируйте неравенство так, чтобы одна сторона была равна нулю. Например, если у вас есть неравенство 2x + 5
- Решите уравнение, полученное в предыдущем шаге. В нашем примере это 2x - 4 = 0. Решив его, получаем x = 2.
- Проверьте, выполняется ли неравенство при найденном значении x. Для этого подставьте значение x в исходное неравенство и проверьте, что оно выполняется. В нашем случае, если подставить x = 2 в исходное неравенство 2x + 5
- Проверьте все остальные возможные значения x, которые могут удовлетворять неравенству. В нашем примере, можно проверить значение x = 1 и x = 3.
Найденные значения целых чисел, при которых неравенство выполняется, являются целыми решениями данного неравенства.
Почему важно найти все целые решения неравенства?

Знание всех целых решений неравенства позволяет в дальнейшем:
| 1. | Получить полное представление о границах возможных значений переменных. |
| 2. | Анализировать и оценивать диапазоны, в которых можно изменять значения переменных. |
| 3. | Производить точные математические доказательства и рассуждения, основанные на знании всех целых решений. |
| 4. | Получить более точные результаты в прикладных задачах, связанных с множествами и диапазонами значений переменных. |
Решение задач, требующих определения всех целых решений неравенства, имеет широкое применение в математике, физике, экономике и других областях науки. Поэтому, важно уметь корректно и точно находить все целые решения неравенств для получения достоверных результатов и сделать правильные выводы из математических моделей и задач.
Методы поиска всех целых решений неравенства
Метод подстановки
Один из самых простых способов найти все целые решения неравенства – это метод подстановки. Сначала определяются границы допустимых значений переменной x, после чего все значения из этого диапазона подставляются в неравенство и проверяется, выполняется ли оно.
- Определение границ: для неравенства ax + b > c, если коэффициент a > 0, то нижняя граница будет -∞, а верхняя граница (c - b - 1) / a; если коэффициент a
- Подстановка и проверка значений: для каждого значения x из диапазона включительно, подставляется в неравенство и проверяется его выполнение. Если выполняется, то x является решением.
Метод графического представления
Еще один способ найти все целые решения неравенства – это метод графического представления. Для этого необходимо построить график левой и правой части неравенства на координатной плоскости. Все целые значения x, для которых левая часть графика находится выше правой части, являются решениями неравенства.
Метод деления диапазона
Еще один метод поиска всех целых решений неравенства – это метод деления диапазона. Для этого необходимо разделить диапазон допустимых значений переменной x на промежутки с целыми значениями. Затем, для каждого промежутка, подставляются значения x в неравенство и проверяется его выполнение. Если выполняется, то все значения x в этом промежутке являются решениями неравенства.
Применение целых решений неравенств в практике
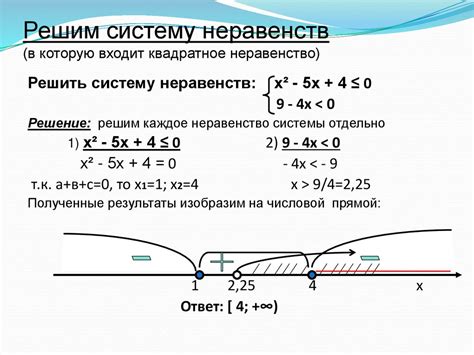
Целые решения неравенств находят широкое применение в различных сферах практики. Это позволяет определить диапазоны значений переменных, удовлетворяющих неравенство, и использовать их для принятия решений или решения задач.
Одной из областей, где целые решения неравенств играют важную роль, является экономика. Например, при планировании бюджета или расчете стоимости проекта, необходимо учитывать ограничения и условия задачи, выраженные в виде неравенств. Найдя все целые решения неравенства, можно определить границы возможных значений переменных, что помогает принять обоснованные решения.
Другой областью, где целые решения неравенств имеют применение, является техническая диагностика и контроль качества. Например, при проверке рабочих параметров оборудования или отборе продукции по заданным требованиям, можно использовать неравенства для определения границ допустимых значений. Поиск целых решений неравенства поможет выявить несоответствия и проблемы в работе.
Также целые решения неравенств могут использоваться в задачах оптимизации. Например, при планировании производства или доставки товаров, необходимо учесть различные ограничения, такие как вес, объем, стоимость и т.д. Поиск всех целых решений неравенств позволяет определить оптимальные варианты и принять эффективные решения.
В заключение, целые решения неравенств играют важную роль в различных сферах практики. Они помогают определить возможные значения переменных в соответствии с ограничениями и условиями задачи. Это позволяет принимать обоснованные решения, решать задачи оптимизации и контролировать качество работ. Поиск всех целых решений неравенств является важным инструментом для достижения эффективных результатов в практических применениях.








