Матрица является одной из важных концепций в линейной алгебре и науке о матрицах. Она используется во многих областях, включая физику, экономику, компьютерную графику и машинное обучение. Одно из ключевых свойств матрицы - ее определенность. Определенность матрицы влияет на ее свойства и поведение в различных операциях и приложениях.
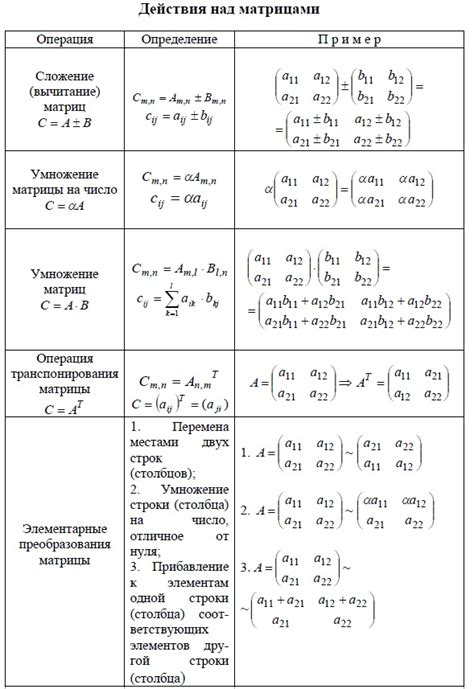
В контексте матриц положительное определение матрицы имеет решающее значение. Когда матрица положительно определена, это означает, что она обладает определенными характеристиками. Положительная определенность матрицы подразумевает, что все ее собственные значения положительны. Это означает, что матрица является положительно определенной.
Такая матрица имеет ряд полезных свойств. Например, она может быть использована для описания эллипсоидальных форм в геометрии и для моделирования случайных процессов. Также положительно определенные матрицы используются в оптимизационных задачах и линейном программировании, где они помогают найти оптимальные решения и улучшить производительность алгоритмов.
Определение положительно определенной матрицы
Иными словами, положительно определенная матрица обладает следующим свойством: для любого ненулевого вектора v его скалярное произведение с матрицей A всегда больше нуля.
Это свойство позволяет говорить о том, что все собственные значения положительно определенной матрицы строго положительны, а ее главные миноры (определители верхних левых подматриц) также положительны.
Положительно определенные матрицы встречаются во многих областях науки и техники, например, в оптимизации, численных методах, статистике, теории управления и др. Они имеют важное значение при решении различных задач, таких как оптимальное распределение ресурсов, аппроксимация функций, моделирование физических процессов и другие.
Критерии положительной определенности
Матрица называется положительно определенной, если для любого ненулевого вектора x выполняется следующее неравенство:
| xT Ax > 0 |
где xT обозначает транспонирование вектора x. Данное неравенство означает, что для любого ненулевого вектора x, его скалярное произведение с матрицей A является положительным числом.
Критерии положительной определенности матрицы A:
- Все собственные значения матрицы A положительны.
- Матрица A является симметричной и положительно определенной.
- Для любой невырожденной подматрицы B матрицы A выполняется неравенство xT Bx > 0 для любого ненулевого вектора x.
Кроме того, положительно определенная матрица A является невырожденной, то есть имеет полный ранг.
Свойства положительно определенных матриц
- Все собственные значения матрицы A больше нуля.
- Для любого ненулевого вектора x, соответствующий квадратичный форма x^T Ax всегда положительно, то есть x^T Ax > 0.
- Матрица A является симметричной и положительно определенной.
Свойства положительно определенных матриц могут быть использованы для решения различных задач в математике и физике. Вот некоторые из них:
| Свойство | Объяснение |
|---|---|
| Уникальность обратной матрицы | Положительно определенная матрица A всегда имеет обратную матрицу A^-1, которая также положительно определена. |
| Критерий минимума | Если A - положительно определенная матрица, то функция f(x) = x^T Ax имеет минимум в точке x = 0. |
| Оценка сходимости | Для положительно определенной матрицы A и любого вектора x, x^T Ax является верхней оценкой для расстояния между итерациями в методе Якоби. |
Исследование свойств положительно определенных матриц играет важную роль в линейной алгебре и находит применение в различных областях науки и техники.
Примеры положительно определенных матриц
Ниже приведены несколько примеров положительно определенных матриц:
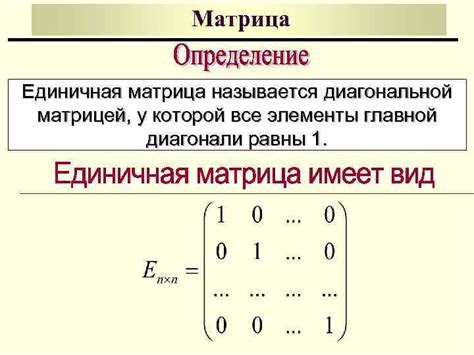
- Единичная матрица. Единичная матрица имеет единицы на главной диагонали и нули в остальных элементах. Она всегда является положительно определенной.
- Матрица Гильберта. Матрица Гильберта имеет элементы, определенные как hij = 1/(i + j - 1), где i и j - индексы строк и столбцов соответственно. Она также является положительно определенной.
- Матрица Вандермонда. Матрица Вандермонда имеет элементы aij = xij-1, где xi - это различные числа. Она является положительно определенной при условии, что xi различны и все положительные.
- Матрица Хилберта. Матрица Хилберта имеет элементы, определенные как hij = 1/(i + j - 1), где i и j - индексы строк и столбцов соответственно. Она также является положительно определенной.
- Матрица Коши. Матрица Коши имеет элементы, определенные как cij = 1/(xi + yj), где xi и yj - некоторые числа. Она является положительно определенной, если числа xi и yj различны и все положительные.
Это лишь несколько примеров из множества положительно определенных матриц. Они имеют важное место в математике и находят широкое применение в дифференциальных уравнениях, приближенных методах и других областях науки и техники.
Симметричность положительно определенной матрицы
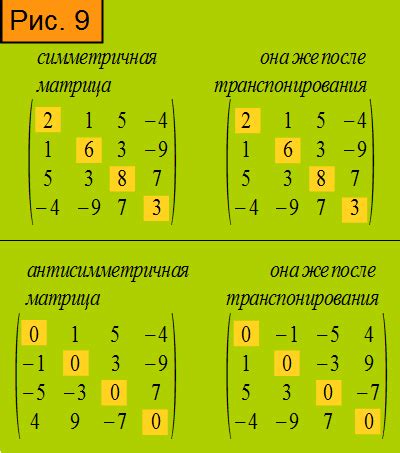
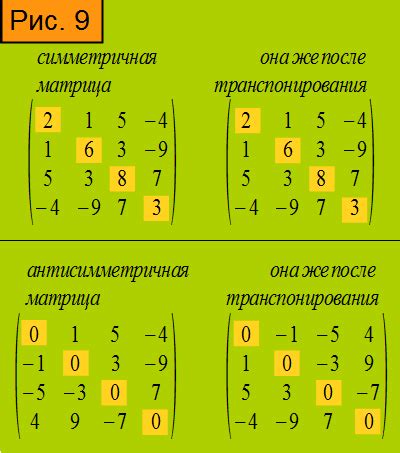
Симметричность матрицы означает, что она равна транспонированной себе: A = A^T, где A – матрица, A^T – транспонированная матрица.
В случае положительно определенной матрицы, симметричность имеет следующий эффект. Пусть A – положительно определенная матрица размера n×n. Тогда существует такая матрица P (также симметричная), что A = P^T × P.
Симметричность матрицы связана с ее собственными значениями. Для симметричной матрицы собственные значения всегда вещественные. Более того, существует ортогональная матрица S, такая что S^T × A × S = D, где D – диагональная матрица с собственными значениями матрицы A на диагонали.
Таким образом, симметричность положительно определенной матрицы позволяет ее спектральное разложение и упрощает анализ ее свойств.
Собственные значения положительно определенной матрицы
Собственное значение матрицы - это число, которое можно получить путем решения уравнения Ax = λx, где A - матрица, x - собственный вектор, а λ - собственное значение.
Для положительно определенной матрицы все собственные значения всегда положительны. Это свойство является следствием самого определения положительно определенной матрицы - все ее собственные значения должны быть положительными.
Собственные значения положительно определенной матрицы играют важную роль во многих областях, таких как оптимизация, анализ данных, теория управления и другие. Они позволяют оценивать и предсказывать различные свойства и характеристики матрицы.
Более того, собственные значения положительно определенной матрицы имеют важные связи с ее собственными векторами. Векторы, соответствующие наибольшим собственным значениям, имеют особую значимость и называются главными осями или главными компонентами матрицы.
Таким образом, собственные значения положительно определенной матрицы предоставляют ценную информацию о ее свойствах и способствуют анализу и пониманию различных процессов и явлений.
Способы определения положительно определенной матрицы
- Определение через собственные значения: Матрица считается положительно определенной, если все ее собственные значения положительны. Собственные значения матрицы можно вычислить с помощью специальных алгоритмов, таких как методы Якоби или степенной метод.
- Определение через индексы: Матрица считается положительно определенной, если все ее главные (или главные диагональные) миноры положительны. Главные миноры могут быть вычислены путем выбора подматрицы из исходной матрицы и определения ее определителя.
- Определение через критерий Сильвестра: Матрица считается положительно определенной, если все ее угловые (верхние левые или нижние правые) миноры положительны и определитель каждой последующей подматрицы также положителен. Критерий Сильвестра позволяет определить положительную определенность матрицы, используя только ее элементы.
Это лишь несколько примеров способов, которые могут быть использованы для определения положительно определенной матрицы. Каждый из этих способов имеет свои преимущества и недостатки, и выбор конкретного метода зависит от конкретной задачи и доступной вычислительной мощности. Важно понимать, что положительно определенная матрица имеет множество интересных свойств и может быть использована в различных областях математики и приложений.
Применение положительно определенных матриц
Положительно определенные матрицы находят широкое применение в различных областях, таких как линейная алгебра, оптимизация, статистика, машинное обучение и др.
Одно из главных применений положительно определенных матриц - решение систем линейных уравнений. Если матрица системы является положительно определенной, то решение системы гарантировано существует и единственно. Это свойство положительно определенных матриц делает их основным инструментом для моделирования и анализа различных физических и экономических процессов.
Еще одним важным применением положительно определенных матриц является их использование в задачах оптимизации. Квадратичная оптимизация, которая сводится к минимизации квадратичной функции, является одной из наиболее распространенных задач в оптимизации. Если матрица квадратичной функции является положительно определенной, то гарантируется наличие и уникальность минимума функции.
Кроме того, положительно определенные матрицы широко используются в статистике и машинном обучении. В задачах регрессии и классификации, положительно определенные матрицы используются для оценки и прогнозирования параметров модели.
Таким образом, положительно определенные матрицы играют важную роль во многих областях современной науки и техники. Их свойства и применение позволяют решать сложные задачи, связанные с моделированием, анализом и оптимизацией различных процессов и явлений.
Алгоритм проверки определенности матрицы

Матрица считается положительно определенной, если все ее главные миноры (миноры, получающиеся из исходной матрицы путем вычеркивания одинаковых строк и столбцов) положительны.
Для проверки определенности матрицы можно использовать следующий алгоритм:
- Начать с исходной матрицы размерности n.
- Проверить значение главного минора порядка 1. Если оно положительное, перейти к следующему шагу, в противном случае матрица не положительно определена.
- Проверить значение главного минора порядка 2. Если оно положительное, перейти к следующему шагу, в противном случае матрица не положительно определена.
- Продолжать проверку главных миноров порядка k, где k = 3, 4, ..., n. Если все главные миноры положительные, то матрица положительно определена, в противном случае - нет.
Используя данный алгоритм, можно определить, является ли матрица положительно определенной. Эта информация может быть полезна при решении различных задач линейной алгебры и оптимизации.








