Поиск корней уравнения – это одна из основных задач математики и науки в целом. Нахождение решений уравнений позволяет понять, как меняется значение переменной при данном соотношении, а также применять эти знания в различных областях жизни. Существует несколько методов, которые помогают найти корень уравнения.
Один из самых простых и распространенных методов – метод подстановки. Суть этого метода заключается в поочередной подстановке предполагаемых значений переменной в уравнение и проверке полученных равенств. Если оно выполняется, значит, это и есть решение уравнения. Если нет, то необходимо выбрать другое предполагаемое значение и повторить процесс.
Еще одним методом, который широко используется для нахождения корней уравнений, является графический метод. Суть этого метода заключается в построении графика функции, заданной уравнением, и определении точек пересечения графика с осью абсцисс. Эти точки и являются корнями уравнения.
Интересно отметить, что для некоторых уравнений можно применить аналитические методы, такие как метод замены переменных, метод дифференцирования или метод группировки членов. Эти методы позволяют найти корень уравнения без необходимости в подстановке значений или построении графика.
Примерами уравнений, которые можно решить с помощью данных методов, являются квадратные уравнения, линейные уравнения, показательные и логарифмические уравнения.
Метод подстановки и его применение

Применение метода подстановки требует знания уравнения и выбора подходящего значения переменной. Значение переменной, которое будет подставлено вместо нее, выбирается на основе анализа уравнения и с учетом удобства вычислений.
Одним из примеров использования метода подстановки может служить уравнение вида ax + b = 0. Подставив значение переменной x = -b/a вместо x в уравнение, мы получим следующее: a(-b/a) + b = 0. Простые вычисления позволяют убедиться, что полученное уравнение верно.
Метод графического представления уравнения
Для использования метода графического представления уравнения необходимо:
- Записать уравнение в виде функции, где искомый корень будет равен нулю;
- Построить график этой функции на координатной плоскости;
- Найти точку пересечения графика с осью абсцисс, которая будет являться корнем уравнения.
Пример:
| Уравнение | График функции | Корень |
|---|---|---|
| x2 - 4 = 0 |  | x = -2, x = 2 |
На графике функции x2 - 4 видно, что пересечение графика с осью абсцисс происходит в точках (-2, 0) и (2, 0), что означает, что корнями уравнения являются значения x = -2 и x = 2.
Следует отметить, что данный метод не всегда применим, особенно в случае сложных функций, где построить график не всегда возможно или требует значительных усилий. Кроме того, метод графического представления может дать только приближенное значение корня и не гарантирует его точности.
Тем не менее, метод графического представления уравнения является полезным инструментом и может быть использован в качестве первоначальной оценки решения уравнения, а также для визуального представления зависимости между переменными.
Метод половинного деления и его эффективность
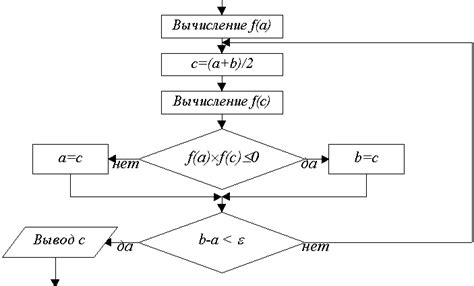
Процесс применения метода половинного деления выглядит следующим образом:
- Выбираются две точки на отрезке [a, b], в котором находится корень уравнения.
- Вычисляется значение функции в середине отрезка, то есть в точке c = (a + b) / 2.
- Если значение функции f(c) близко к нулю (близко к тому, что означает, что c - приближение к корню), то алгоритм завершается и c считается корнем уравнения.
- Если значение f(c) имеет противоположный знак с f(a), то корень уравнения находится в левой половине отрезка, и алгоритм повторяется для отрезка [a, c].
- Если значение f(c) имеет противоположный знак с f(b), то корень уравнения находится в правой половине отрезка, и алгоритм повторяется для отрезка [c, b].
- Шаги 2-5 повторяются до тех пор, пока не будет достигнута требуемая точность или не будет найдено приближенное значение корня.
Метод половинного деления обеспечивает сходимость к корню уравнения, но при этом скорость сходимости является относительно низкой. Тем не менее, этот метод выполняет надежное и устойчивое приближение корня, особенно когда уравнение является непрерывным и монотонным.
Эффективность метода половинного деления зависит от шага сокращения отрезка и заданной точности. Чем меньше шаг сокращения и чем более точное значение корня необходимо найти, тем больше итераций потребуется для вычисления корня. Поэтому при использовании метода половинного деления важно настроить эти параметры для достижения оптимальной эффективности и точности вычисления.
Метод итераций: поиск корня путем последовательных приближений
Для применения метода итераций необходимо привести уравнение к виду x = g(x), где g(x) - некоторая функция.
Итерационный процесс начинается с выбора начального приближения x_0. Затем, на каждой итерации, используется следующее приближение:
x_(n+1) = g(x_n)
Процесс продолжается до тех пор, пока разность между двумя последовательными точками станет достаточно малой, то есть когда выполняется условие:
|x_(n+1) - x_n| < ε
где ε - некоторая заданная точность.
При правильном выборе функции g(x) и начального приближения x_0, метод итераций сходится к корню уравнения. Однако необходимо быть осторожным, так как некорректный выбор функции или начального приближения может привести к расходимости итерационного процесса.
Применение метода итераций широко распространено в различных областях, включая численные методы, оптимизацию и решение уравнений.








