Что значит решить треугольник: основные методы и примеры

Что значит решить треугольник: основные методы и примеры

Вычисление параметров треугольника - одна из основных задач геометрии. Для этого нужно найти значения его сторон и углов. Решать треугольник можно разными способами, в зависимости от известных данных и требуемых результатов.

Один из простейших методов - использование теоремы Пифагора. Если известны длины двух сторон треугольника, можно найти длину третьей стороны, применив формулу a^2 + b^2 = c^2, где a и b - известные стороны, а c - неизвестная сторона.

Если известны сторона и два угла треугольника, можно использовать теорему синусов. Эта теорема позволяет найти длины остальных сторон и неизвестные углы. Формула теоремы: a / sin(A) = b / sin(B) = c / sin(C), где a, b, c - стороны треугольника, A, B, C - соответствующие углы.

Пример решения треугольника: известны сторона a = 5, угол B = 30° и угол C = 60°. По формуле теоремы синусов, получаем a / sin(A) = b / sin(B) = c / sin(C). Известные углы: A = 180° - B - C = 90°. Подставляя значения в формулу, получаем 5 / sin(90°) = b / sin(30°) = c / sin(60°). Упрощая выражение, находим, что b = 5 * sin(30°) / sin(90°) = 2.5, и c = 5 * sin(60°) / sin(90°) = 4.33. Таким образом, получаем стороны треугольника: a = 5, b = 2.5 и c = 4.33.

Это лишь несколько основных методов решения треугольников. Существует еще множество других способов, включая применение теоремы косинусов, формул Герона, правил прямоугольных треугольников и многое другое. Знание и умение решать треугольники является необходимым для решения многих задач различных областей, включая геометрию, физику и инженерию.

Понятие решения треугольника

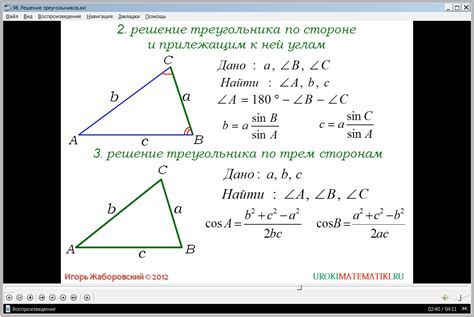
Для решения треугольника обычно используются такие факты, как равенство суммы углов треугольника 180 градусам и свойства треугольников, такие как теорема синусов и теорема косинусов.

Существует несколько методов решения треугольников, включая:

Методы нахождения сторон:

Использование теоремы Пифагора для прямоугольного треугольника;
Использование теоремы косинусов для треугольников с известными углами и сторонами;
Использование равенства площадей смежных треугольников для треугольников с общей стороной.

Методы нахождения углов:

Использование теоремы синусов;
Использование теоремы косинусов;
Использование равенства суммы углов треугольника 180 градусам.

Решение треугольника позволяет определить его геометрические свойства и использовать эти знания в различных областях, включая геометрию, физику, инженерные и архитектурные расчеты и т. д.

Основные методы решения треугольника

Метод с использованием известных сторон и углов:
- Теорема косинусов позволяет найти длину стороны треугольника, если известны длины двух других сторон и между ними расположен угол.
- Теорема синусов позволяет найти длину стороны треугольника, если известны длины двух других сторон и соответствующие углы при них.
- Теорема косинусов и синусов также позволяют найти значения углов треугольника.
Метод с использованием известных сторон и высот:
- Теорема Пифагора позволяет находить длину стороны треугольника, если известны высота, проведенная к этой стороне, и длины других двух сторон.
- Зная длины сторон треугольника и высоту, можно также вычислить площадь треугольника.
Метод с использованием известных величин, таких как площадь, радиус окружности, описанной вокруг треугольника:
- Формула Герона позволяет находить площадь треугольника по длинам его сторон.
- Формула радиуса вписанной окружности позволяет находить радиус окружности, вписанной в треугольник, по его площади и полупериметру.
- Формула радиуса описанной окружности позволяет находить радиус окружности, описанной вокруг треугольника, по длинам его сторон.

Это лишь некоторые из методов, которые применяются при решении треугольника. В зависимости от предоставленных данных и искомых характеристик, можно выбрать наиболее удобный метод для решения конкретной задачи.

Метод синусов и его применение

Суть метода заключается в следующем: используя три соотношения синусов, можно найти значения сторон и углов треугольника, если известны лишь определенные данные.

Для применения метода синусов необходимо знать значение хотя бы одной стороны треугольника и значения двух углов, или значения двух сторон и значение одного угла.

Процесс решения треугольника методом синусов состоит из следующих шагов:

Исходя из имеющихся данных, определить, какие соотношения синусов можно использовать для решения.
Выразить неизвестные величины через известные по формулам синусов.
Решить полученные уравнения и найти значения неизвестных.
Проверить полученные данные и привести их в нужный формат.

Метод синусов может быть применен для решения различных задач, включая нахождение сторон треугольника по известным углам, определение углов треугольника по известным сторонам, а также нахождение высоты или медианы треугольника.

Пример решения треугольника методом синусов:

Дано: сторона a = 5 см, угол B = 45°, угол C = 60°.
Используя соотношение синусов, выразим стороны b и c через известные значения a и углы B и C:
- sin(B) = b / a
- sin(C) = c / a
Подставив известные значения, получим:
- sin(45°) = b / 5
- sin(60°) = c / 5
Решив полученные уравнения, найдем значения b и c.
Проверим полученные данные и приведем их к нужному формату.

Таким образом, метод синусов является эффективным инструментом для решения треугольников и может быть использован в различных задачах, связанных с нахождением сторон и углов треугольников.

Метод косинусов и его преимущества

Основным преимуществом метода косинусов является его универсальность - он может быть применен для решения различных типов треугольников, включая прямоугольные и остроугольные треугольники. Кроме того, данный метод позволяет найти все стороны и углы треугольника, что делает его очень полезным для решения задач со сложными условиями.

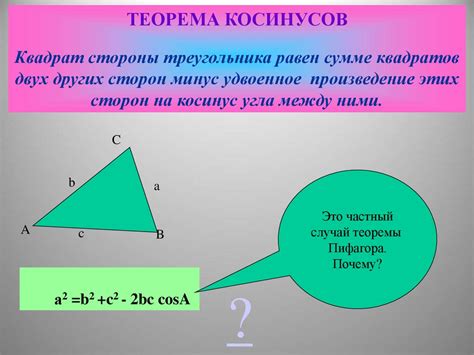
Для применения метода косинусов необходимо знание формул, связывающих стороны и углы треугольника с косинусами. Наиболее часто используемая формула имеет вид:

a² = b² + c² - 2bc * cos(A)

где a, b и c - стороны треугольника, A - угол между сторонами b и c.

Используя данную формулу, можно найти значение недостающей стороны или угла треугольника, подставив известные значения в формулу и решив уравнение относительно искомого значения.

Примеры применения метода косинусов могут включать такие задачи, как нахождение длины стороны треугольника при известных длинах двух других сторон и угла между ними, или нахождение значения угла треугольника при известных длинах двух сторон и значениями углов.

Теорема Пифагора и его роль в решении треугольника

Формула теоремы Пифагора выглядит следующим образом:

a² + b² = c²

Здесь a и b представляют длины катетов, а c - длину гипотенузы.

Теорема Пифагора является одним из основных способов определить отсутствующую сторону или угол в прямоугольном треугольнике. По-сути, она позволяет нам связать длины сторон треугольника с его углами, что делает возможным решение множества задач связанных с треугольниками.

Для решения треугольника с использованием теоремы Пифагора, необходимо знать длины двух сторон треугольника. Затем мы можем использовать формулу теоремы Пифагора, чтобы решить третью сторону. Например, если мы знаем длину двух катетов, мы можем использовать формулу теоремы Пифагора, чтобы найти длину гипотенузы.

Важно отметить, что теорема Пифагора применима только к прямоугольным треугольникам, где один из углов равен 90 градусам. Если треугольник не является прямоугольным, теорему Пифагора нельзя использовать, и для решения треугольника потребуется использование других методов, таких как теоремы синусов и косинусов.

Решение треугольника при помощи тригонометрической формулы

Для начала, необходимо знать значения двух сторон и одного угла треугольника. Далее, можно использовать формулы для нахождения остальных сторон и углов.

Например, если известны сторона a, сторона b и угол C треугольника ABC, можно использовать следующие формулы:

a	b	C
c = √(a^2 + b^2 - 2ab * cos(C))	A = sin^(-1)((a * sin(C)) / c)	B = 180 - A - C

где:

a, b, c - стороны треугольника
A, B, C - углы треугольника
√ - квадратный корень, ^ - возведение в степень
sin - синус угла, cos - косинус угла, tan - тангенс угла
sin^(-1) - обратная функция синуса

Таким образом, при помощи тригонометрической формулы можно решить треугольник, зная значения двух сторон и одного угла. При этом необходимо помнить о правильной последовательности применения формул и о необходимости подстановки значений в правильные места формулы.

Примеры решения треугольника по известным данным

Решение треугольника может быть выполнено для различных известных данных, таких как длины сторон треугольника, значения углов или комбинация обоих. Далее приведены примеры решения треугольника для различных сценариев.

1. Решение по длинам сторон:

Известны длины всех трех сторон треугольника.
Для решения можно использовать теорему косинусов или правило синусов.
Найденные значения углов могут быть использованы для дальнейших вычислений или анализа треугольника.

2. Решение по значениям углов:

Известны значения всех трех углов треугольника.
Для решения можно использовать теорему синусов или теорему косинусов.
Находятся значения длин сторон или другие характеристики треугольника, в зависимости от поставленной задачи.

3. Сочетание известных данных:

Известны длины сторон и значение одного угла (или нескольких).
Могут быть использованы соответствующие формулы и методы для нахождения других значений.
Результирующая информация может включать значения длин сторон, углов или других характеристик треугольника.

Примеры решения треугольника демонстрируют различные способы применения формул и методов, а также позволяют получить полезную информацию о треугольнике на основе имеющихся данных.

Преимущества и ограничения разных методов решения треугольника

Метод синусов

Один из наиболее распространенных методов решения треугольника – метод синусов. Этот метод основан на использовании соотношения между стороной треугольника и синусом противолежащего ей угла. Преимуществами этого метода являются:

Простота и удобство использования;
Возможность решения треугольника даже при отсутствии информации о угле между двумя известными сторонами;
Возможность решения треугольника при наличии информации о углах, но отсутствии информации о сторонах.

Однако, метод синусов имеет и свои ограничения:

Необходимость знания как минимум двух сторон и одного угла;
При неправильном выборе сторон может возникнуть ситуация, когда синус больше 1 или меньше -1, что приводит к отсутствию ответа.

Метод косинусов

Метод косинусов основан на использовании соотношения между стороной треугольника и косинусом угла, смежного с этой стороной. Преимущества метода косинусов:

Простота и удобство использования;
Возможность решения треугольника даже при отсутствии информации о угле между двумя известными сторонами;
Возможность решения треугольника при наличии информации о углах, но отсутствии информации о сторонах.

Ограничения метода косинусов:

Необходимость знания как минимум двух сторон и одного угла;
При неправильном выборе сторон может возникнуть ситуация, когда косинус больше 1 или меньше -1, что приводит к отсутствию ответа.

Метод тангенсов

Метод тангенсов основан на использовании соотношения между сторонами треугольника и тангенсами углов. Преимущества метода тангенсов:

Простота и удобство использования;
Возможность решения треугольника при наличии информации только о сторонах, без знания углов.

Ограничения метода тангенсов:

Необходимость знания как минимум двух сторон или углов;
Если тангенс угла равен бесконечности, то ответа не существует.

Как решить треугольник: основные методы и алгоритмы