Решение круговых примеров — это одна из базовых навыков, которые дети учат во втором классе. Круговые примеры представляют собой задачи, в которых требуется найти значение неизвестной величины в круговом уравнении. При решении таких задач необходимо применять специальные методы и приемы, которые позволяют точно найти ответ.
Один из основных методов решения круговых примеров второго класса — это использование свойства равенства суммы всех углов треугольника 180 градусов. Для этого необходимо записать уравнение, в котором все известные углы суммируются и приравниваются к 180 градусам. Затем требуется найти значение неизвестного угла, подставив известные значения и решив полученное уравнение.
Еще один метод решения круговых примеров — использование свойства равенства противоположных углов. Если в круге даны два равных угла, значит, их противоположные углы тоже равны. Поэтому, зная значение одного из углов, можно найти значение противоположного угла с помощью простой замены.
Круговые примеры второго класса: общая информация и методы решения
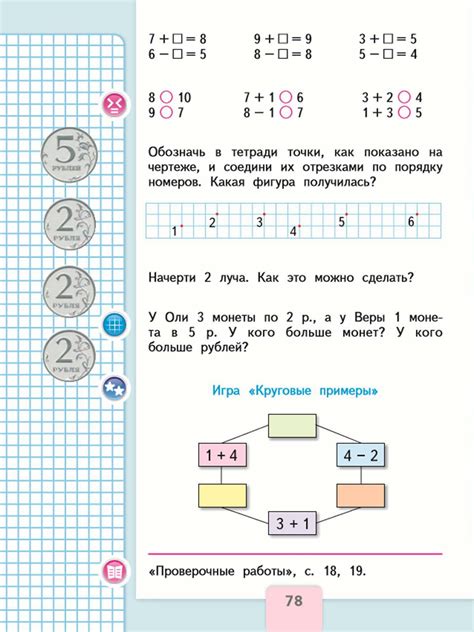
Для решения круговых примеров второго класса необходимо знать основные формулы и правила. Важно помнить, что круг - это фигура с закругленными границами, у которой центр и радиус. При решении задач можно использовать следующие методы:
- Нахождение длины окружности. Для этого необходимо знать формулу длины окружности: длина окружности = 2 * π * радиус.
- Нахождение площади круга. Для этого нужна формула площади круга: площадь круга = π * радиус^2.
- Нахождение радиуса круга. Этот метод требует знания длины окружности: радиус = длина окружности / 2π.
Применяя эти методы, можно решать различные задачи, связанные с кругами. Например, найти длину окружности, если известен радиус, или наоборот, найти радиус, если известна длина окружности.
Решение круговых примеров второго класса помогает развить логическое мышление, умение анализировать информацию и применять знания математики на практике.
Решение круговых примеров с помощью дробей
Для решения круговых примеров, необходимо знать, что круг делится на 360 градусов. Таким образом, каждый градус представляет собой 1/360 круга. Это позволяет представить градусы в виде обыкновенной дроби.
Например, чтобы решить пример "найдите угол, который составляет 120 градусов с целым кругом", мы можем записать это в виде дроби: 120/360. Далее, мы можем упростить эту дробь, разделив числитель и знаменатель на их общий делитель - 120 и 360 делятся на 120, поэтому мы получим 1/3.
Теперь, используя полученную дробь, мы можем ответить на вопрос: "угол, который составляет 120 градусов с целым кругом, равен 1/3 круга".
Таким образом, решение круговых примеров с помощью дробей позволяет более точно и точно определить углы и другие круговые величины. Этот метод особенно полезен при работе с более сложными круговыми примерами и геометрическими задачами.
Метод решения круговых примеров с использованием процентов
Метод решения круговых примеров с использованием процентов основан на представлении чисел в виде процентных долей.
Для решения таких примеров, необходимо:
- Выяснить, какую часть от целого составляет каждое число в примере.
- Представить эти доли в процентах.
- Произвести необходимые вычисления.
Приведем пример:
Задача: Вова выпил из сока 25% от всего количества сока в бутылке, а Маша выпила 30%. Сколько сока осталось в бутылке?
Решение:
- Выясним, какую часть от целого составляет каждое число: 25% = 0.25 и 30% = 0.30.
- Вычтем из 100% доли, которые выпили Вова и Маша: 100% - (25% + 30%) = 45%.
- Представим полученную долю в виде числа: 45% = 0.45.
- Умножим полученную долю на общее количество сока в бутылке: 0.45 * целое количество сока в бутылке = остаток сока в бутылке.
Таким образом, чтобы найти остаток сока в бутылке, необходимо умножить 0.45 на целое количество сока в бутылке.
Ответ: Осталось 45% сока в бутылке.
Круговые примеры с применением пропорции
Для решения круговых примеров второго класса можно использовать метод пропорции. Этот метод позволяет определить значение неизвестной величины, основываясь на уже известной информации.
Пропорция можно записать в виде:
известное значение : неизвестное значение = известное значение : неизвестное значение
Рассмотрим пример:
У Васи есть кукла, а у его сестры - гнездышко с яйцами. Если у сестры 4 яйца, то сколько яиц будет, если кукол будет 6?
Решение:
Мы знаем, что кукол 6, а яиц - неизвестное значение. Тогда пропорцию можно записать в виде:
4 : Неизвестное значение = 6 : 1
Чтобы найти неизвестное значение, нужно выполнить следующие действия:
4 * 1 = 6 * Неизвестное значение
Неизвестное значение = 6 * 1 / 4 = 6 / 4 = 1.5
Ответ: если у Васи будет 6 кукол, то у его сестры будет 1.5 гнездышка с яйцами.
Метод Герона для решения круговых примеров
S = π * r * r
- S - площадь круга
- π - число пи, примерно равное 3.14159
- r - радиус круга
Для решения круговых примеров второго класса с помощью метода Герона нужно знать радиус круга и уметь умножать числа.
Пример:
- Пусть радиус круга равен 5 сантиметров.
- Подставим значение радиуса в формулу: S = 3.14159 * 5 * 5
- Выполним умножение: S = 3.14159 * 25
- Произведем вычисление: S ≈ 78.54
Таким образом, площадь круга с радиусом 5 сантиметров примерно равна 78.54 квадратным сантиметрам.
Обратные круговые примеры: как их решать
| Метод | Описание | Пример |
|---|---|---|
| 1. Обратный ход | Ученик должен начать с ответа и "откатиться" по шагам назад, выполняя обратные действия для каждого шага примера. | Пример: Если в круговом примере ученику дано результат 36 и осталось выполнить последнее действие, то он должен понять, какое действие приводит к данному результату. Например, если ответ получается путем умножения, то обратное действие будет деление. |
| 2. Подстановка вариантов | Ученик может попробовать разные варианты чисел, подставлять их вместо переменных в примере и проверять, приводит ли это к нужному результату. | Пример: Если в примере есть два числа, он может попробовать различные комбинации чисел и проверить, дает ли это нужное значение при последовательном выполнении всех операций. |
| 3. Решение в обратном порядке | Ученик может начать с последнего действия и выполнять операции в обратном порядке, пока не получит исходные числа. | Пример: Если в круговом примере результат известен, ученик может начать с последней операции и выполнять обратное действие в обратном порядке до получения исходных чисел. |
Подходящий метод решения выбирается в зависимости от сложности примера и индивидуальных предпочтений ученика. Решение обратных круговых примеров помогает развивать у ученика логическое мышление, аналитические навыки и умение применять основные математические операции.
Примеры решения сложных круговых заданий с использованием формулы площади круга
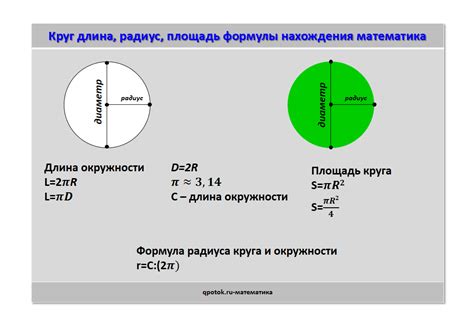
Если вам дан круговой пример второго класса, в котором нужно найти площадь круга, вы можете воспользоваться следующей формулой:
S = πr²
Где S - площадь круга, π - математическая константа, примерное значение которой равно 3.14, а r - радиус круга.
Давайте рассмотрим пример:
У нас есть круг с радиусом 5 см. Чтобы найти его площадь, мы должны воспользоваться формулой:
S = πr²
Подставим в формулу значение радиуса:
S = 3.14 × 5²
S = 3.14 × 25
S ≈ 78.5
Таким образом, площадь данного круга примерно равна 78.5 квадратных сантиметров.
Теперь вы знаете, как использовать формулу площади круга для решения сложных круговых заданий второго класса.
Метод алгебры для решения круговых примеров
Для применения метода алгебры нужно следовать нескольким шагам:
- Записать известные значения, используя переменные или цифры.
- Записать известное математическое выражение, используя переменные и операции сложения и вычитания.
- Решить полученное выражение, находя значение неизвестной переменной.
Возьмем, например, следующий пример:
8 + ? = 15
Для решения этого примера по методу алгебры сначала запишем известные значения. Число 8 - это известное значение, а знак вопроса обозначает неизвестное значение, которое мы будем находить.
Затем запишем математическое выражение с использованием переменной и операции сложения:
8 + x = 15
Далее решим полученное выражение, находя значение неизвестной переменной. Для этого вычтем из обеих частей уравнения число 8:
x = 15 - 8
Выполнив вычисления, получим ответ:
x = 7
Таким образом, решение примера будет равно x = 7.
Метод алгебры позволяет решать круговые примеры второго класса, используя алгебраические операции. Он является универсальным и может быть использован для решения различных типов примеров.
Интерактивные упражнения для тренировки решения круговых примеров
Вот несколько примеров интерактивных упражнений:
- Круговые головоломки: здесь ученикам предлагается решить головоломку, состоящую из нескольких круговых примеров. Они должны найти правильные ответы и расположить их в правильном порядке, чтобы решить головоломку.
- Круговые задачи: в этих упражнениях ученикам предлагается решить задачу, используя круговые примеры. Например, им может быть предложено найти периметр или площадь круга, зная его радиус или диаметр.
- Круговые игры: такие игры помогают ученикам применить свои знания о круговых примерах в практических ситуациях. Например, им может быть предложено сделать круговой пазл или игру на нахождение правильного ответа на круговой вопрос.
Интерактивные упражнения включают использование различных наглядных материалов, таких как круги, цветные карточки и игровые доски. Это помогает ученикам визуализировать круговые примеры и легче понять их решение.
Тренировка с использованием интерактивных упражнений также может быть забавной и увлекательной для учеников, что помогает им лучше усваивать материал и развивать интерес к математике.
Подводя итог, интерактивные упражнения представляют собой эффективный способ тренировки и развития навыков решения круговых примеров для учеников второго класса. Они активизируют мышление и помогают лучше понять математические понятия, связанные с круговыми примерами.








