Математическая функция является важным объектом изучения в различных областях науки, включая математический анализ, экономику, физику и многие другие. Одно из ключевых свойств функции - ее форма. Одним из наиболее распространенных свойств формы функции является выпуклость. В контексте функций, выпуклость означает, что график функции на отрезке между двумя точками лежит ниже или на высоте отрезка, соединяющего эти две точки.
Для определения выпуклости функции воспользуемся понятием касательной к графику функции. Если функция задана на интервале (a, b), то ее график можно изобразить на координатной плоскости. Касательная к графику функции в точке x является прямой, которая касается графика функции в этой точке и имеет ту же наклонную как и функция в этой точке. Если для любых двух точек на графике функции интервал между ними лежит ниже этой функции, то функция является выпуклой на этом интервале. Если выполняется обратное условие, то функция является вогнутой на этом интервале.
Примером выпуклой функции является функция f(x) = x^2. Ее график - парабола, которая открывается вверх. Это означает, что для любых двух точек на графике функции, интервал между ними лежит ниже самой функции. Примером вогнутой функции является функция g(x) = -x^2. Ее график - парабола, которая открывается вниз. Для этой функции выполняется обратное условие - для любых двух точек на графике функции интервал между ними лежит выше самой функции.
Определение функции
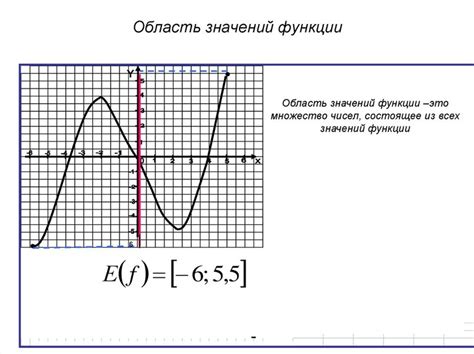
Формально, функция может быть определена следующим образом: для каждого элемента из множества X, называемого областью определения функции, функция сопоставляет элемент из множества Y, называемого областью значений функции.
Обозначение функции может быть различным, например, f(x), g(t), h(y) и т.д. Здесь x, t, y - это переменные, которые могут принимать значения из области определения функции.
Важным свойством функции является ее однозначность. Это означает, что каждому элементу из области определения соответствует только один элемент из области значений. Если функция не обладает этим свойством, она называется многозначной функцией.
Кроме того, функцию можно представить графически. График функции - это множество точек в пространстве, каждая из которых имеет координаты (x, f(x)). Графическое представление функции позволяет наглядно визуализировать ее поведение и исследовать различные свойства.
Определение выпуклости
Математическая функция называется выпуклой, если все точки, лежащие на ее графике, лежат или выше касательных к графику, или на самом графике. Формально, функция f(x) называется выпуклой на интервале I, если для любых точек x1 и x2 из I и для любого значения t из отрезка [0,1] выполняется неравенство:
f((1-t)x1 + tx2) ≤ (1-t)f(x1) + tf(x2)
где (1-t)x1 + tx2 - взвешанное среднее значение между x1 и x2.
Другими словами, если для любых двух точек на графике функции лежащих на интервале I, отрезок между этими точками лежит, или выше графика функции.
Функция выпукла
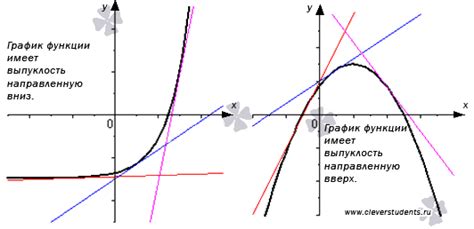
Функция называется выпуклой, если ее график на любом отрезке, соединяющем две точки графика, лежит выше этого отрезка или на нем. Другими словами, если для любых двух точек на графике исходной функции выполняется условие:
f(λx + (1 - λ)y) ≤ λf(x) + (1 - λ)f(y),
где 0 ≤ λ ≤ 1, то функция является выпуклой.
Интуитивно функция выпукла, если все точки ниже хорды соединяющей две любые точки графика лежат ниже самой хорды. В случае строгой выпуклости каждая точка будет лежать выше хорды (либо на хорде). Если условие выпуклости в обоих направлениях обращается в строгое неравенство функция называется строго выпуклой.
Примером функции, которая является выпуклой, может служить парабола с положительным коэффициентом при квадрате переменной. Например:
| x | f(x)=x^2 |
|---|---|
| −3 | 9 |
| −2 | 4 |
| −1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
Как видно из таблицы, добавление точек на график может создать линию, которая лежит выше графика исходной функции, поэтому функция f(x)=x^2 является выпуклой.
Пример выпуклой функции
Для иллюстрации понятия выпуклой функции, рассмотрим следующий пример:
- Пусть дана функция
f(x) = x^2. - Мы можем проверить, является ли эта функция выпуклой, применив определение выпуклости.
- Для этого сначала возьмем две произвольные точки на графике функции, скажем,
(x_1, f(x_1))и(x_2, f(x_2)). - Затем мы можем проверить, лежит ли отрезок, соединяющий эти две точки, ниже графика функции.
- Если отрезок полностью лежит ниже графика функции, то функция является выпуклой.
- В нашем примере, если мы возьмем произвольные точки
(x_1, f(x_1))и(x_2, f(x_2)), мы увидим, что отрезок, соединяющий эти точки, всегда будет лежать ниже графика функцииf(x) = x^2. - Таким образом, мы можем заключить, что функция
f(x) = x^2является выпуклой.
Этот пример демонстрирует, как проверить, является ли функция выпуклой, но в реальности существует много других типов функций, которые также могут быть выпуклыми.
Свойства выпуклых функций
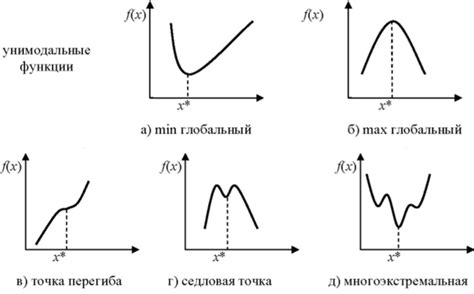
Выпуклая функция обладает несколькими важными свойствами:
- Любое сечение выпуклой функции с вертикальной прямой будет выпуклым отрезком или пустым множеством. Это свойство называется выпуклостью снизу.
- Если функция выпукла, то для любых точек a и b на ее графике и любого числа t от 0 до 1, точка (ta + (1-t)b, tf(a) + (1-t)f(b)) также будет находиться на графике функции. Это свойство называется свойством выпуклости.
- Любая выпуклая функция на некотором открытом интервале будет непрерывной на этом интервале.
- Первая производная выпуклой функции не убывает на ее области определения.
- Вторая производная выпуклой функции неотрицательна на ее области определения. Если вторая производная строго положительна, то функция называется строго выпуклой.
Знание этих свойств помогает в анализе и оптимизации функций, а также в решении задач выпуклого программирования.
Функция не выпукла
- Линейная функция: y = ax + b, где a ≠ 0.
- Экспоненциальная функция: y = abx, где a > 0 и 0
- Логарифмическая функция: y = loga(x), где a > 1.
Во всех этих примерах графики функций имеют вогнутые или впавшие вниз части, что делает их не выпуклыми. Такие функции могут иметь увеличивающиеся значения скорости роста на некоторых промежутках, а затем замедлять рост.
Пример функции с невыпуклой областью

Функция f(x) = x^3 представляет собой пример функции с невыпуклой областью.
Для определения выпуклости функции необходимо проанализировать ее вторую производную. Если вторая производная положительна на всей области определения функции, то функция является выпуклой. Если вторая производная отрицательна на всей области определения функции, то функция является вогнутой.
В случае функции f(x) = x^3 вторая производная равна f''(x) = 6x. Вторая производная положительна на всей числовой прямой, за исключением точки x = 0, где она равна нулю. Таким образом, область определения функции f(x) = x^3 является невыпуклой.
На графике функции видно, что она имеет точку перегиба в точке x = 0. Левая часть графика функции вогнута вверх, а правая часть - вниз. Поэтому функция f(x) = x^3 имеет невыпуклую область, где меняется выпуклость функции.








