Функция удовлетворяет уравнению: основные понятия и примеры

Функция – это важное понятие в математике. Она определяет зависимость одного набора значений от другого. Функции широко используются в различных областях: в физике, экономике, информатике и других. Одним из основных способов описания функций является уравнение, которое позволяет определить набор входных и выходных значений функции.

Уравнение функции представляет собой математическое выражение, в котором присутствуют переменные и константы. Это выражение указывает на зависимость функции от одной или нескольких переменных. Часто уравнение функции представляется в виде y = f(x), где y – зависимая переменная, а x – независимая переменная. Функция f(x) определяет правило соответствия между значениями x и y. Например, уравнение y = 2x описывает линейную функцию, удовлетворяющую прямой пропорциональности.

Важно отметить, что функции могут быть различных типов и иметь разные уравнения. Некоторые функции являются алгебраическими (например, полиномы), другие – тригонометрическими (например, синус или косинус), третьи – экспоненциальными (например, экспоненциальная функция). Хорошим примером уравнения функции может служить уравнение окружности x^2 + y^2 = r^2, где x и y – независимые переменные, а r – радиус окружности.

Основная цель изучения функций и их уравнений заключается в понимании закономерностей и взаимосвязей между переменными. Это позволяет математикам и другим специалистам решать различные задачи, моделировать реальные явления и предсказывать их развитие. Изучение функций и их уравнений является неотъемлемой частью математического анализа и алгебры, а также находит применение в различных учебных курсах и профессиональных областях.

Что такое функция?

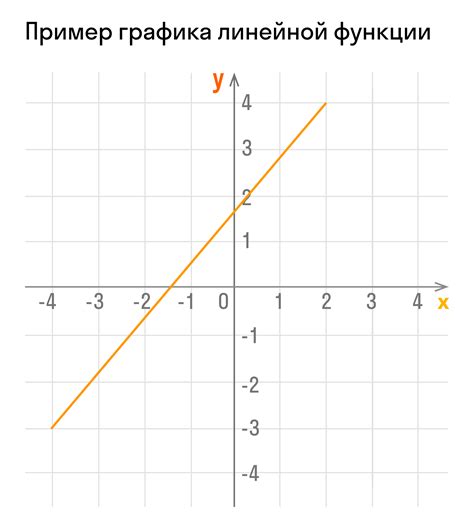
Функция f: X → Y,

где X – множество всех возможных аргументов (область определения), Y – множество всех возможных значений (область значений).

Функция часто обозначается как y = f(x), где переменная x – это аргумент функции, а y – соответствующее значение. Например, функция y = 2x описывает увеличение значения y вдвое относительно значения x.

Функция может иметь разные свойства, такие как монотонность, периодичность, непрерывность и другие. Также функции могут быть представлены в различных математических формах, таких как алгебраические, тригонометрические, показательные и логарифмические.

Примеры функций:

Линейная функция: y = kx + b
Квадратичная функция: y = ax^2 + bx + c
Тригонометрическая функция: y = sin(x)
Логарифмическая функция: y = log(x)

Функции широко используются в различных научных и технических областях, таких как физика, экономика, компьютерные науки и другие. Они позволяют анализировать и моделировать различные процессы, предсказывать значения и принимать решения на основе имеющихся данных.

Основные понятия функции

Домен функции – это множество всех возможных значений аргументов функции. Он определяет, для каких значений аргументов функция определена.
Область значений – это множество всех возможных значений функции. Она определяет, какие значения могут быть получены при подстановке аргументов в функцию.
График функции – это графическое представление функции на плоскости. Он показывает зависимость значений функции от значений аргументов.
Линейная функция – это функция, график которой представляет собой прямую линию. Её уравнение имеет вид y = kx + b, где k и b – постоянные коэффициенты.
Квадратичная функция – это функция, график которой представляет собой параболу. Её уравнение имеет вид y = ax^2 + bx + c, где a, b и c – постоянные коэффициенты.

Это лишь некоторые из основных понятий, связанных с функциями. Изучение функций позволяет анализировать и описывать различные явления и процессы в математике, физике, экономике и других областях науки и жизни.

Уравнение и его связь с функцией

В свою очередь, функция – это правило, которое сопоставляет каждому элементу из одного множества (аргументу) элемент из другого множества (значение функции). Можно сказать, что функция задает зависимость между двумя множествами.

Связь между уравнением и функцией заключается в том, что уравнение может задавать зависимость между аргументом и значением функции. То есть, если мы знаем уравнение, то можем определить, какому значению соответствует определенный аргумент.

Например, рассмотрим уравнение f(x) = 2x + 3, где f(x) обозначает функцию, а 2x + 3 – ее аргумент. Здесь уравнение показывает, что значение функции равно двум значением аргумента плюс три. То есть, для каждого значения аргумента, функция принимает определенное значение.

Аргумент, x	Значение функции, f(x)
1	5
2	7
3	9

Таким образом, уравнение и функция тесно связаны друг с другом. Уравнение задает зависимость между аргументом и значением функции, а функция, в свою очередь, может быть выражена через уравнение. Знание уравнения позволяет нам определить, какое значение функции соответствует определенному аргументу.

Условия существования функции

Для того чтобы функция существовала, необходимо, чтобы выполнялись определенные условия. Основные условия, которым должна удовлетворять функция, включают в себя:

1. Определенность: функция должна быть определена для каждого значения аргумента в ее области определения. В противном случае, функция будет недействительна или неопределена в некоторых точках.

2. Единственность: каждому значению аргумента должно соответствовать только одно значение функции. Если одному и тому же значению аргумента могут соответствовать разные значения функции, то функция не будет являться однозначной.

3. Получение значений: для каждого значения аргумента, функция должна возвращать соответствующее значение функции. Если для какого-то значения аргумента функция не возвращает значение, то функция будет неполной или неопределенной.

4. Отображение: функция должна быть отображением, то есть каждому значению аргумента должно соответствовать некоторое значение функции. Если функция не является отображением, то она будет недействительна.

Всякий раз, когда одно из этих условий нарушается, функция может быть некорректной или неопределенной в некоторых точках.

Примеры функций

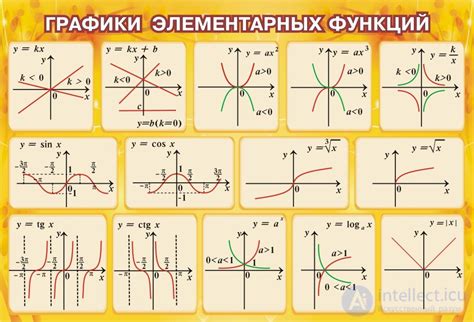
Функция	Описание	Пример
Линейная функция	График функции представляет собой прямую линию	f(x) = 2x + 3
Квадратичная функция	График функции представляет собой параболу	f(x) = x^2 + 2x + 1
Тригонометрическая функция	Функция, которая связывает угол с его тригонометрическими значениями	f(x) = sin(x)
Экспоненциальная функция	Функция, график которой имеет вид экспоненциальной кривой	f(x) = e^x

Это лишь некоторые из множества доступных функций в математике. Функции широко применяются в различных науках и инженерии для описания и моделирования различных явлений и процессов.

Линейная функция

Коэффициент k называется наклоном прямой, а коэффициент b - свободным членом.

Линейная функция имеет множество примеров в реальной жизни. Например, если мы представим время (x) в часах и расстояние (y) в километрах, то уравнение y = 60x будет описывать скорость автомобиля, который движется со скоростью 60 км/ч. Другой пример - уравнение y = 2x + 5 описывает зависимость стоимости (y) от количества килограммов (x) конфет.

График линейной функции - это прямая линия на координатной плоскости. Наклон прямой показывает, насколько быстро или медленно значение y изменяется в зависимости от изменения значения x. Если наклон положительный, то значение y увеличивается с увеличением значения x, а если наклон отрицательный, то значение y уменьшается с увеличением значения x.

Квадратичная функция

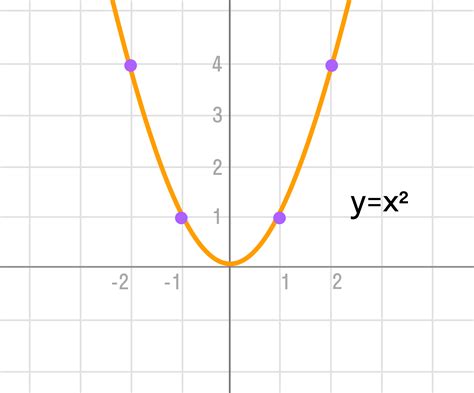
Квадратичная функция имеет следующие особенности:

График квадратичной функции представляет собой параболу.
Если а > 0, то парабола открывается вверх, если а
Вершина параболы – точка максимума или минимума функции.
Квадратичная функция может иметь один или два корня, в зависимости от дискриминанта.
Уравнение f(x) = 0 называется квадратным уравнением, которое можно решить с помощью формулы дискриминанта.
При а = 0 функция становится линейной.
Квадратичные функции широко применяются в физике, экономике и других науках для моделирования различных процессов и явлений.

Примеры квадратичных функций:

f(x) = x^2
f(x) = -2x^2 + 3x - 5
f(x) = 4x^2 + 1

Изучение квадратичных функций является важной частью алгебры и математического анализа.

Показательная функция

Основными свойствами показательной функции являются:

Если a > 1, то график функции возрастает. Если a
Значение функции при x = 0 равно 1.
Если a > 1, то при x стремящемся к бесконечности, значение функции также стремится к бесконечности. Если a

Примеры показательной функции:

f(x) = 2^x
g(x) = 3^x
h(x) = 0.5^x

Тригонометрическая функция

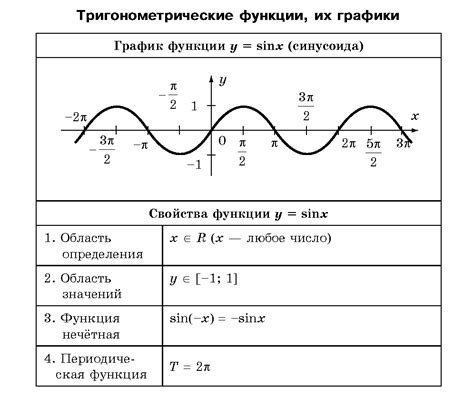
Основные тригонометрические функции включают синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc).

Синус угла - это отношение противоположной стороны к гипотенузе. Например, sin(x) = a / c, где a - противоположная сторона, c - гипотенуза и x - угол.

Косинус угла - это отношение прилежащей стороны к гипотенузе. Например, cos(x) = b / c, где b - прилежащая сторона, c - гипотенуза и x - угол.

Тангенс угла - это отношение противоположной стороны к прилежащей стороне. Например, tan(x) = a / b, где a - противоположная сторона, b - прилежащая сторона и x - угол.

Котангенс угла - это отношение прилежащей стороны к противоположной стороне. Например, cot(x) = b / a, где b - прилежащая сторона, a - противоположная сторона и x - угол.

Секанс угла - это отношение гипотенузы к прилежащей стороне. Например, sec(x) = c / b, где c - гипотенуза, b - прилежащая сторона и x - угол.

Косеканс угла - это отношение гипотенузы к противоположной стороне. Например, csc(x) = c / a, где c - гипотенуза, a - противоположная сторона и x - угол.

Тригонометрические функции широко применяются в математике, физике, инженерии и других областях для решения различных задач, связанных с изучением углов и их свойств.

Логарифмическая функция

Логарифмическая функция записывается в виде:

$$y = \log_{a}{x}$$

где $x$ - аргумент функции (положительное число), $a$ - основание логарифма (положительное число, отличное от 1), $y$ - значение функции.

Основное свойство логарифмической функции заключается в том, что она позволяет найти значение показателя степени, при котором данное основание $a$ возводится, чтобы получить аргумент $x$. То есть, если

$$x = a^y$$

то