Что значит выразить вектор через два других вектора

В линейной алгебре существует возможность выражать один вектор через два других вектора. Это важное понятие позволяет сделать выводы о линейной зависимости векторов и понять, как один вектор может быть представлен в виде комбинации других векторов.

Основной метод, используемый в этом случае, называется линейной комбинацией. Линейная комбинация векторов представляет собой их линейную комбинацию с использованием различных коэффициентов.

Например, пусть у нас есть два вектора, A и B. Чтобы выразить вектор C через векторы A и B, мы можем использовать следующую формулу: C = k*A + m*B, где k и m - коэффициенты, определяющие взаимное положение векторов.

Однако стоит отметить, что выражение вектора через другие векторы не всегда возможно. Если векторы линейно независимы, то существует только тривиальное решение, когда коэффициенты равны нулю. В противном случае, если векторы линейно зависимы, то мы можем найти некоторые ненулевые коэффициенты, для которых выражение справедливо.

Вектор как базовое понятие

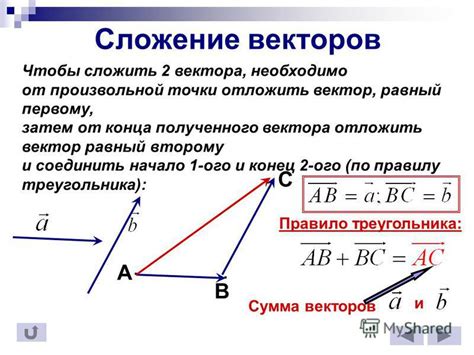
Векторы могут служить для представления различных физических величин, таких как сила, скорость, ускорение. Они являются базовыми понятиями в физике и математике и нашли широкое применение в разных областях науки и техники.

Вектор может быть представлен в виде упорядоченной пары или набора чисел, которые образуют его компоненты. В зависимости от контекста, векторы могут быть двумерными, трехмерными или иметь другую размерность.

Векторы можно складывать, вычитать, умножать на число, находить их скалярное произведение и векторное произведение. Также можно определить длину вектора, его направление и нормализовать его. Векторы могут быть представлены графически с помощью стрелок, которые указывают направление и длину.

Методы выражения вектора через два других вектора

Существует несколько методов выражения вектора через два других вектора. Рассмотрим некоторые из них:

1. Метод проекций.

Суть метода заключается в вычислении проекций исходного вектора на два заданных вектора. Для этого используется формула проекции вектора на другой вектор. По найденным проекциям можно восстановить исходный вектор.

2. Метод линейной комбинации.

Этот метод основан на представлении исходного вектора как линейной комбинации двух других векторов. Для этого нужно найти такие коэффициенты, при умножении на которые исходные векторы суммируются и дают нужный вектор.

3. Метод векторного произведения.

Этот метод применяется в трехмерном пространстве и основан на свойствах векторного произведения. С помощью этого метода можно выразить исходный вектор через два других вектора, найдя их векторное произведение.

4. Метод матриц.

Для этого метода используется матричная форма записи векторов. Система линейных уравнений, составленная на основе матричной формы, позволяет найти коэффициенты исходного вектора и, соответственно, выразить его через два других вектора.

Все эти методы используются для вычисления координат исходного вектора по заданным векторам. Они широко применяются в линейной алгебре и физике для решения различных задач, связанных с векторами.

Метод разложения вектора по базису

Базисные векторы образуют базис векторного пространства. Базис является набором линейно независимых векторов, которые позволяют представить любой вектор данного векторного пространства. Каждый вектор этого пространства может быть представлен в виде линейной комбинации базисных векторов.

Для разложения вектора по базису необходимо найти коэффициенты линейной комбинации, с помощью которых можно представить исходный вектор. Эти коэффициенты называются компонентами вектора по базису.

Чтобы найти компоненты вектора по базису, необходимо составить уравнение, в котором каждое слагаемое будет соответствовать одному из базисных векторов, умноженному на соответствующий ему коэффициент. Затем, решив это уравнение, можно получить значения компонент вектора по базису.

Метод разложения вектора по базису широко используется в различных областях науки и техники. Он является основой для решения многих задач, связанных с работой с векторами и векторными пространствами.

Метод модуля и направления вектора

Модуль вектора - это длина вектора и обозначается обычно символом |AB|. Чтобы найти модуль вектора, можно воспользоваться теоремой Пифагора:

|AB| = √(x^2 + y^2),

где x и y - координаты конца вектора AB.

Направление вектора можно определить с помощью угла, который он образует с положительным направлением оси OX. В геометрическом отношении это направление на плоскости будем обозначаться угловой мерой φ, а в координатной форме – наклоном к абсциссе.

Вектор можно представить в виде суммы двух векторов по формуле:

AB = |AB| · cos φ · i + |AB| · sin φ · j,

где |AB| - модуль вектора, cos φ - косинус угла между вектором AB и положительным направлением оси OX, sin φ - синус этого угла, i и j - орты, направленные вдоль осей OX и OY соответственно.

Метод модуля и направления вектора применяется для нахождения вектора через известные величины его модуля и направления.

Основные понятия выражения вектора через два других вектора

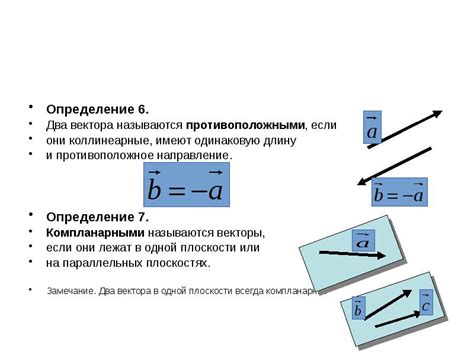
Чтобы выразить вектор AB через два других вектора AC и AD, необходимо определить соответствующие коэффициенты. Для этого можно использовать методы решения систем линейных уравнений или геометрический подход.

Методы выражения вектора через два других вектора

1. Метод решения систем линейных уравнений:
   • Составить систему из трех уравнений, где каждое уравнение представляет собой координатное равенство для вторичных векторов и заданного вектора.
   • Решить систему уравнений для определения значений коэффициентов.
   • Подставить найденные значения коэффициентов в линейную комбинацию и выразить вектор AB через векторы AC и AD.
2. Геометрический метод:
   • Построить параллелограмм на векторах AC и AD.
   • Провести диагональ параллелограмма, соединяющую начало AB с серединой противоположной стороны.
   • Вектор AB можно представить как сумму векторов AC и AD, противоположного вектора проведенной диагонали.

Выражение вектора через два других вектора является важным инструментом в линейной алгебре и геометрии. Оно позволяет более удобно и эффективно работать с векторными операциями и исследовать различные свойства векторов.

Линейная независимость векторов

Пусть даны n векторов: v₁, v₂, ..., v_n. Если существуют такие коэффициенты c₁, c₂, ..., c_n, что уравнение c₁v₁ + c₂v₂ + ... + c_nv_n = 0 имеет только тривиальное решение (т.е. c₁ = c₂ = ... = c_n = 0), то векторы v₁, v₂, ..., v_n являются линейно независимыми.

Если же существуют такие коэффициенты c₁, c₂, ..., c_n, что уравнение c₁v₁ + c₂v₂ + ... + c_nv_n = 0 имеет нетривиальное решение (т.е. хотя бы один из коэффициентов не равен нулю), то векторы v₁, v₂, ..., v_n являются линейно зависимыми.

Если в системе векторов есть линейно зависимые векторы, то можно один из них выразить через комбинацию других векторов с ненулевыми коэффициентами.

Линейная зависимость векторов

Векторы называются линейно зависимыми, если можно найти такие числа (коэффициенты), для которых линейная комбинация этих векторов равна нулевому вектору.

Математически это можно записать в виде:

a1*v1 + a2*v2 + ... + an*vn = 0

где ai - коэффициенты, и v1, v2, ..., vn - векторы.

В случае линейной зависимости можно выразить один из векторов через другие, используя алгоритм Гаусса или метод Грама-Шмидта.

Линейно независимые векторы, наоборот, не могут быть выражены через другие векторы линейной комбинацией.

Метод Гаусса-Жордана для выражения вектора через два других вектора

Для начала, векторы, которые нужно использовать для выражения другого вектора, записываются в матричном виде:

A = [ a₁₁, a₁₂, ..., a_1n]

B = [ b₁₁, b₁₂, ..., b_1n]

C = [ c₁₁, c₁₂, ..., c_1n]

Так как вектор C нужно выразить через векторы A и B, то создаем матрицу из этих векторов:

| a₁₁ a₁₂ ... a_1n |

| b₁₁ b₁₂ ... b_1n |

| c₁₁ c₁₂ ... c_1n |

Далее, применяем элементарные преобразования строк, чтобы привести матрицу к треугольному виду. В результате, получим матрицу вида:

| 1 0 ... 0 |

| 0 1 ... 0 |

| 0 0 ... 1 |

Теперь, чтобы выразить вектор C через векторы A и B, нужно записать полученные коэффициенты при каждом элементе исходных векторов. В данном случае, вектор C будет равен:

C = c₁₁ * A + c₁₂ * B

Таким образом, метод Гаусса-Жордана позволяет выразить вектор через два других вектора, применяя элементарные преобразования строк матрицы. Этот метод является простым и эффективным способом нахождения неизвестных коэффициентов при векторах.