Что значит вписанный треугольник

Вписанный треугольник – это треугольник, который полностью содержится внутри другого геометрического фигуро. Эта фигура может быть, например, окружностью, кругом или другим многоугольником, но наиболее распространенным случаем является вписанный треугольник внутри окружности. Такой треугольник обладает определенными особенностями и свойствами, которые делают его интересным объектом изучения для специалистов по геометрии и математике.

Одной из особенностей вписанного треугольника является то, что его вершины лежат на окружности. Точки пересечения сторон треугольника, продолженных за их концы, называются точками соприкосновения треугольника с окружностью. Именно эти точки образуют вписанный треугольник. Кроме того, в вписанном треугольнике каждый угол является вписанным углом, то есть лежит на окружности. Это свойство позволяет строить различные геометрические заключения и рассуждения, которые находят широкое применение в различных науках и практических областях.

Если вписанный треугольник является равносторонним, то и окружность, в которую он вписан, является равносторонней.

Вписанный треугольник также имеет массу уникальных свойств, которые помогают изучать и анализировать его. Одно из таких свойств – это то, что сумма всех трех вписанных углов в треугольнике всегда равна 180 градусам. Это это связано с тем, что дуги, образованные этими углами на окружности, в сумме составляют полный оборот в 360 градусов. Еще одно особенное свойство вписанного треугольника – это то, что длины его сторон могут быть использованы для вычисления радиуса окружности, в которую он вписан.

Определение вписанного треугольника

Такой тип треугольника имеет ряд особенностей. Например, вписанный треугольник обладает равными углами, соответствующими хордам, и обратная теорема Пифагора справедлива для его сторон.

Вписанный треугольник широко применяется в геометрических задачах и теоремах. Его свойства позволяют решать различные задачи, такие как нахождение длины стороны треугольника или его углов. Вставление вписанного треугольника внутрь окружности может служить основой для решения сложных геометрических задач.

Изучение вписанного треугольника особенно полезно при решении задач с использованием теории окружностей и геометрических конструкций. Он является важным элементом геометрии и находит свое применение не только в учебных заданиях, но и в реальной жизни, например, при рисовании круговых дуг или определении местоположения точек на окружности.

Пример вписанного треугольника

Что такое вписанный треугольник: основные характеристики

1. Срединный перпендикуляр. Любая сторона вписанного треугольника делит окружность на две равные дуги, а середина этой стороны лежит на срединном перпендикуляре, проходящем через центр окружности.

Например, если AB – сторона вписанного треугольника, то срединный перпендикуляр к AB проходит через центр окружности, и точка его пересечения с окружностью называется точкой C.

2. Углы вписанного треугольника. Сумма углов вписанного треугольника равна 180 градусам. Каждый угол вписанного треугольника равен половине соответствующей центральной дуги, отсекаемой на окружности.

Например, если угол BAC вписанного треугольника, то он равен половине дуги BC на окружности.

3. Полярное соотношение. Для вписанного треугольника справедливо полярное соотношение – произведение сторон треугольника на синусы соответствующих противолежащих углов равно диаметру описанной окружности.

Например, для вписанного треугольника ABC с диаметром окружности, равным d, верно следующее соотношение: AB * sin C + BC * sin A + AC * sin B = d.

Зная эти основные характеристики вписанного треугольника, можно проводить различные геометрические рассуждения и выявлять взаимосвязи с другими элементами фигуры или конструкции, в которой он находится.

Формула для вычисления вписанного треугольника

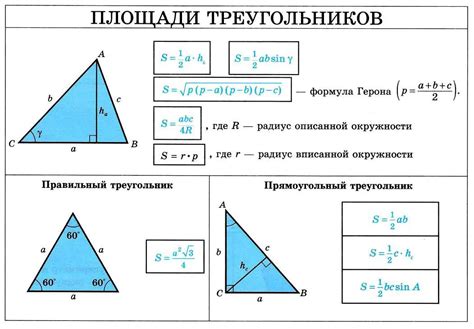
Чтобы вычислить параметры вписанного треугольника, необходимо знать радиус окружности, в которую он вписан. Формула для вычисления радиуса окружности, в которую вписан треугольник, выглядит следующим образом:

R = a/(2*sin(A/2)) = b/(2*sin(B/2)) = c/(2*sin(C/2))

где:

• R - радиус окружности, в которую вписан треугольник;
• a, b, c - стороны треугольника;
• A, B, C - углы треугольника.

Для вычисления углов вписанного треугольника существуют следующие формулы:

A = 2 * arcsin(a/(2 * R))

B = 2 * arcsin(b/(2 * R))

C = 2 * arcsin(c/(2 * R))

где:

• A, B, C - углы вписанного треугольника;
• a, b, c - стороны треугольника;
• R - радиус окружности, в которую вписан треугольник.

Используя эти формулы, можно точно вычислить параметры вписанного треугольника, зная его стороны либо радиус окружности, в которую он вписан.

Особенности вписанного треугольника

Одной из особенностей вписанного треугольника является то, что его углы, образованные сторонами треугольника и хордами окружности, имеют определенные соотношения. А именно, сумма углов, образованных на одной и той же дуге окружности, равна 180 градусов.

Другой важной особенностью вписанного треугольника является то, что стороны треугольника и хорды окружности, соответствующие этим сторонам, также имеют определенные соотношения. Например, если a, b и c - стороны треугольника, а r - радиус описанной окружности, то по теореме синусов выполняется равенство a/sin(A) = b/sin(B) = c/sin(C) = 2r, где A, B и C - соответствующие углы треугольника.

Кроме того, вписанный треугольник имеет ряд других свойств. Например, середины сторон вписанного треугольника образуют отрезок, который параллелен одной из сторон треугольника. Также, если сегмент окружности, определенный двумя сторонами вписанного треугольника, делит третью сторону треугольника на отрезки a и b, то a*b = c^2, где c - третья сторона треугольника.

Геометрические свойства вписанного треугольника

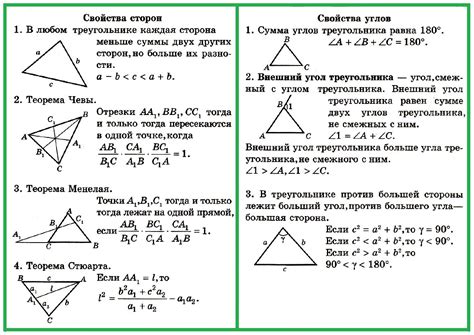
1. Углы вписанного треугольника: Углы вписанного треугольника равны половине меры дуги, опирающейся на этот угол. То есть, если угол треугольника опирается на дугу, имеющую меру α, то угол будет иметь меру α/2.

2. Треугольник, вписанный в окружность, внутри которой находится прямая, называется 'инсцрибированным'. Сумма углов вписанного треугольника равна 180 градусам, то есть треугольник инсцрибированный.

3. Длины сторон вписанного треугольника: Длины сторон вписанного треугольника можно выразить через радиус окружности, в которую вписан данный треугольник. Длина каждой стороны треугольника равна произведению радиуса окружности на синус половины меры угла треугольника.

4. Формула радиуса окружности: Радиус окружности, вписанной в треугольник, может быть выражен через площадь треугольника и полупериметр. Формула: Радиус окружности = (Площадь треугольника) / (Полупериметр треугольника).

5. Теорема о касательных: Вершины вписанного треугольника лежат на касательных, проведенных из вершин этого треугольника к окружности. Данная теорема соотносит углы между касательной и значением углов в треугольнике.

Существование вписанного треугольника: условия

Владея определенными свойствами, треугольник может оказаться вписанным в окружность. Для того чтобы треугольник можно было назвать вписанным, должны выполняться следующие условия:

Если треугольник удовлетворяет этим двум условиям, то он называется вписанным. Вписанный треугольник имеет множество интересных свойств и связей с окружностями, которые изучаются в геометрии.

Основные применения вписанного треугольника

В геометрии вписанный треугольник может использоваться для вычисления различных параметров и углов треугольника. Например, если известны углы треугольника и радиус окружности, на которой он вписан, то можно вычислить длины его сторон.

Одним из основных применений вписанного треугольника является решение задач связанных с построением. Например, если известны радиус окружности и две ее хорды, можно построить вписанный треугольник по этим данным. Вписанный треугольник также может использоваться для построения других геометрических фигур, например, октаэдра или икосаэдра.

Также вписанный треугольник имеет важное значение в тригонометрии. Соотношения между сторонами и углами вписанного треугольника позволяют вычислять значения тригонометрических функций. Это особенно важно при решении задач, связанных с треугольниками и тригонометрией.

Таким образом, вписанный треугольник имеет широкий спектр применений в геометрии, построении и тригонометрии. Изучение его свойств и особенностей позволяет решать различные задачи и получать новые знания о геометрических фигурах и их свойствах.

Примеры вписанных треугольников

Вписанные треугольники встречаются в различных геометрических фигурах и имеют свои особенности. Рассмотрим несколько примеров:

1. Вписанный треугольник в окружность. Треугольник называется вписанным, если все его вершины лежат на окружности. В таком треугольнике сумма двух углов при основании всегда равна измерению третьего угла.

2. Вписанный треугольник в квадрат. В таком случае, одна из сторон треугольника будет совпадать с одной из сторон квадрата. Такой треугольник имеет свойство, что сумма длин двух его сторон всегда больше третьей стороны.

3. Вписанный треугольник в прямоугольник. В этом случае, одна из сторон треугольника совпадает с одной из сторон прямоугольника. Треугольник, вписанный в прямоугольник, является прямоугольным и имеет свойства прямоугольного треугольника.

Это лишь некоторые примеры вписанных треугольников, их существует гораздо больше. Вписанные треугольники широко используются в геометрии и имеют множество интересных свойств и особенностей.

Пример вписанного треугольника в окружность

Возьмем в качестве примера треугольник ABC. Все его вершины лежат на окружности с центром O. Тогда ACB - вписанный треугольник. Вписанный треугольник имеет следующие свойства:

• Сумма углов, опирающихся на одну из дуг окружности, равна 180 градусов.
• Углы, образованные двумя хордами на одной и той же дуге окружности, равны.
• Продолжения сторон вписанного треугольника, лежащие за окружностью, пересекаются в одной точке - центре окружности.
• Если известны два угла вписанного треугольника, то третий угол всегда определяется однозначно.

Изучение особенностей и свойств вписанного треугольника позволяет решать различные задачи, связанные с геометрией и окружностями. Это важное понятие, которое применяется не только в геометрии, но и в других областях науки и техники.

Вписанный треугольник: пример в геометрическом изображении

В геометрии вписанным называется треугольник, все вершины которого лежат на окружности.

Примером вписанного треугольника может служить следующая ситуация:

1. Нарисуем окружность и выберем случайную точку на её окружности.
2. Проведем две хорды, проходящие через выбранную точку.
3. Точки пересечения хорды с окружностью будут вершинами вписанного треугольника.

Таким образом, получаем треугольник, все вершины которого лежат на окружности, и он называется вписанным треугольником.

Вписанные треугольники имеют множество интересных свойств и используются в различных математических задачах и доказательствах.