Векторы - это важное понятие в математике и физике. Они представляют собой объекты, которые обладают как магнитудой (длиной), так и направлением. Векторы могут быть представлены как стрелки, которые указывают на определенную точку в пространстве.
Одной из важных характеристик векторов является их взаимная перпендикулярность. Когда два вектора перпендикулярны, их направления образуют прямой угол. Это означает, что их скалярное произведение равно нулю.
Определение взаимной перпендикулярности векторов играет важную роль во многих областях, таких как геометрия, физика и инженерия. Концепция перпендикулярности позволяет нам решать различные задачи, связанные с векторами, такие как нахождение вектора, параллельного или перпендикулярного данному, а также определение угла между векторами.
Изучение векторов и их взаимной перпендикулярности позволяет нам лучше понять и описать различные физические явления и математические законы. Понимание этой концепции является фундаментальным для успешного решения задач, связанных с векторами и их применением в различных областях науки и техники.
Что такое векторы?
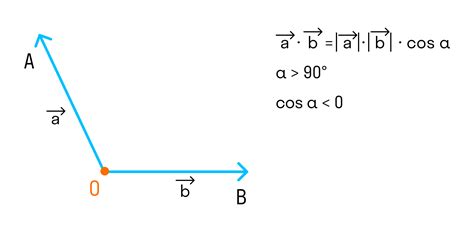
Векторы часто используются для описания таких физических величин, как сила, скорость и перемещение. Например, вектор силы может указывать направление и величину силы, действующей на тело.
Векторы могут быть представлены в виде графических отрезков с началом и концом, а также в виде упорядоченных пар чисел, называемых координатами. Координаты вектора могут представлять направление и величину вектора относительно определенной системы координат.
Векторы могут быть сложены, вычитаны или умножены на число. Сложение векторов выполняется путем сложения соответствующих координат или графическим методом параллелограмма. Умножение вектора на число дает новый вектор, имеющий тот же направление, но измененную величину.
Векторы часто используются в геометрии для определения симметрии и перпендикулярности. Два вектора считаются перпендикулярными, если их скалярное произведение равно нулю. Перпендикулярные векторы образуют прямые углы друг с другом и могут быть использованы для определения перпендикулярных линий и плоскостей.
| Операция | Описание |
|---|---|
| Сложение векторов | Сложение соответствующих координат или графический метод параллелограмма |
| Вычитание векторов | Вычитание соответствующих координат или графический метод параллелограмма |
| Умножение вектора на число | Умножение каждой координаты вектора на число |
| Скалярное произведение векторов | Умножение соответствующих координат векторов и их сложение |
Векторы являются важным инструментом в математике и физике, и их понимание позволяет решать различные задачи, связанные с движением и взаимодействием объектов.
Определение и примеры
Перпендикулярные векторы – это такие векторы, которые образуют прямой угол друг с другом. То есть, если два вектора перпендикулярны, то угол между ними равен 90 градусов.
Примеры перпендикулярных векторов:
- Вектор, направленный вдоль оси x (Ox) и вектор, направленный вдоль оси y (Oy) на координатной плоскости. Эти два вектора являются перпендикулярными и образуют прямой угол друг с другом.
- Вектор, направленный вдоль диагонали квадрата и вектор, направленный вдоль одной из его сторон. Эти векторы также являются перпендикулярными и образуют прямой угол друг с другом.
- Векторы силы тяжести и нормальной силы на горизонтальной поверхности. Эти векторы перпендикулярны друг другу, так как сила тяжести направлена вниз, а нормальная сила направлена вперед по поверхности.
Понимание перпендикулярности векторов позволяет решать множество задач в физике и математике, а также применять их в практике.
Виды векторов
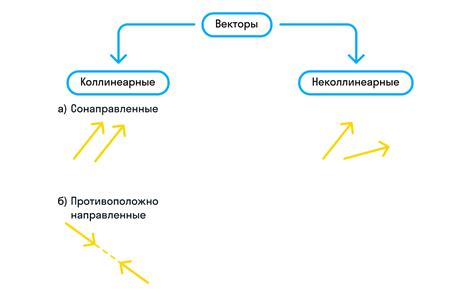
Векторы также могут быть классифицированы по направлению: прямолинейные и противоположно направленные. Прямолинейные векторы имеют одно и то же направление, а противоположно направленные векторы находятся в противоположных направлениях.
Еще одним признаком для классификации векторов является положение их начала и конца. Коллинеарные векторы имеют общее начало и лежат на одной прямой, а неколлинеарные векторы могут иметь разное начало и распологаться в пространстве произвольно.
Также векторы могут быть классифицированы по ориентации на плоскости. Координатные оси образуют базис на плоскости, и векторы могут быть положительно или отрицательно ориентированными относительно этих осей.
Наконец, векторы могут быть классифицированы по своей функциональности. Векторы могут быть физическими, математическими, экономическими и т. д., в зависимости от области, в которой они применяются.
Операции над векторами
Векторы могут подвергаться различным операциям, которые позволяют выполнять вычисления с этими величинами.
Основными операциями над векторами являются:
- Сложение векторов. Для сложения векторов необходимо складывать соответствующие компоненты каждого вектора. Полученный в результате сложения вектор обладает свойством коммутативности и ассоциативности.
- Вычитание векторов. Процесс вычитания векторов аналогичен сложению, только вместо сложения выполняется вычитание компонент.
- Умножение вектора на скаляр. При умножении вектора на скаляр все компоненты вектора умножаются на этот скаляр. Результатом является новый вектор, имеющий ту же направленность, но измененную длину.
- Скалярное произведение. Скалярное произведение двух векторов определяется как произведение модулей векторов и косинуса угла между ними.
- Векторное произведение. Векторное произведение двух векторов определяется как вектор, перпендикулярный плоскости, в которой лежат исходные векторы. Модуль вектора определяется как произведение модулей исходных векторов на синус угла между ними.
Операции над векторами являются основой для решения множества задач в физике, математике и других науках. Понимание этих операций позволяет более глубоко изучать различные аспекты векторных величин и их применение в практике.
Как определить взаимную перпендикулярность векторов?
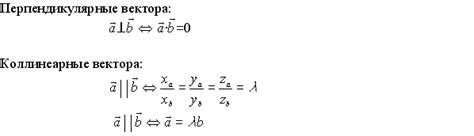
Два вектора называются взаимно перпендикулярными, если они образуют прямой угол друг с другом. Это означает, что векторы могут быть расположены так, что их начала совпадают, а концы образуют прямой угол.
Существуют несколько методов определения взаимной перпендикулярности векторов:
- Геометрический метод: построение. Для определения взаимной перпендикулярности векторов, можно построить графическое представление этих векторов на плоскости или в пространстве. Если полученные отрезки образуют прямой угол, то векторы являются взаимно перпендикулярными.
- Аналитический метод: скалярное произведение. Векторы a и b взаимно перпендикулярны, если их скалярное произведение равно нулю. Скалярное произведение векторов определяется как произведение сумм их соответствующих координат.
- Аналитический метод: векторное произведение. Векторы a и b взаимно перпендикулярны, если их векторное произведение равно нулю. Векторное произведение векторов определяется как произведение длин векторов на синус угла между ними.
Определение взаимной перпендикулярности векторов имеет важное значение во многих областях, включая геометрию, физику и инженерные науки. Знание этого понятия позволяет проводить различные расчеты, решать задачи и делать выводы о взаимосвязи векторов в пространстве.
Теоретическое объяснение
Для определения взаимной перпендикулярности двух векторов необходимо проверить, чтобы их скалярное произведение равнялось нулю. Скалярное произведение двух векторов вычисляется как сумма произведений их координат. Если результат этой операции равен нулю, то это означает, что векторы перпендикулярны друг другу.
Методы определения
Существует несколько методов для определения взаимной перпендикулярности векторов:
- Геометрический метод:
- Визуальное представление векторов на графике и проверка их ортогональности с помощью измерения углов между ними.
- Проверка перпендикулярности векторов с помощью векторного произведения.
- Проверка перпендикулярности векторов с помощью скалярного произведения.
- Аналитический метод:
- Расчет скалярного произведения векторов и проверка его равенства нулю.
- Расчет векторного произведения векторов и проверка его равенства нулевому вектору.
Выбор метода определения взаимной перпендикулярности векторов зависит от задачи и доступных средств анализа. Важно учитывать, что перпендикулярность векторов является особенно важным свойством при решении многих геометрических и физических задач.
Геометрическая интерпретация
Перпендикулярность двух векторов геометрически интерпретируется как отсутствие у них общих точек, кроме начала координат. Если два вектора перпендикулярны, то они образуют прямой угол друг с другом. Это означает, что они расположены таким образом, что прямая, проходящая через их начало координат, делит их на две равные части.
Геометрическая интерпретация векторов и их перпендикулярности позволяет легко визуализировать их свойства и отношения друг к другу. Это важно для понимания многих геометрических и физических концепций и является основой векторного анализа.
Примеры

Рассмотрим несколько примеров, чтобы лучше понять, что такое векторы и как определить их взаимную перпендикулярность.
- Пример 1:
- Пример 2:
Пусть у нас есть два вектора A и B. Вектор A имеет координаты (2, 4) и вектор B имеет координаты (-4, 2). Для определения взаимной перпендикулярности этих векторов, мы можем воспользоваться свойством их скалярного произведения. Если скалярное произведение векторов A и B равно нулю, то они являются перпендикулярными. Выполним расчет:
A * B = (2 * -4) + (4 * 2) = -8 + 8 = 0
Таким образом, наши векторы A и B являются перпендикулярными.
Рассмотрим два вектора C и D. Вектор C имеет координаты (3, 2) и вектор D имеет координаты (1, -8). Для проверки их перпендикулярности, также воспользуемся скалярным произведением:
C * D = (3 * 1) + (2 * -8) = 3 - 16 = -13
В данном случае, скалярное произведение векторов C и D не равно нулю, следовательно, они не являются перпендикулярными.
Таким образом, скалярное произведение векторов помогает нам определить их взаимную перпендикулярность и применять этот прием в различных математических дисциплинах.








