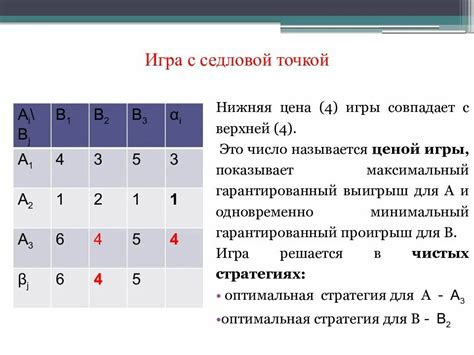
Седловая точка матрицы является важным понятием в линейной алгебре. Она представляет собой элемент матрицы, который является наименьшим в своей строке и наибольшим в своем столбце. Таким образом, седловая точка матрицы является пересечением определенной строки и столбца, где элемент имеет экстремальное значение.
Определение седловой точки матрицы помогает в анализе и решении задач, связанных с оптимизацией и нахождением экстремумов. Седловые точки используются в различных областях науки и техники, включая экономику, информатику, физику и многое другое. Они играют важную роль при решении задач оптимизации и принятии решений.
Примером седловой точки матрицы может служить следующая матрица 3x3:
8 5 2 1 9 8 7 6 3
В данном примере седловыми точками являются числа 8 и 3. 8 является наибольшим в своем столбце (в первом столбце) и наименьшим в своей строке (во второй строке). 3 является наименьшим в своей строке (в третьей строке) и наибольшим в своем столбце (в третьем столбце).
Определение седловой точки матрицы
Другими словами, если в матрице найдется элемент, который является максимумом в своей строке и минимумом в своем столбце, то этот элемент будет седловой точкой матрицы.
Седловая точка матрицы - это элемент, который имеет наименьшее значение в своем столбце и наибольшее значение в своей строке. Она является пересечением столбца и строки, где все другие элементы этих областей меньше или равны ей.
Седловых точек может быть несколько в матрице или не быть вовсе. Возможна ситуация, когда седловой точки в матрице нет, в таком случае говорят, что матрица не имеет седловых точек.
Приведенная ниже таблица демонстрирует пример матрицы с седловой точкой:
| Столбец 1 | Столбец 2 | Столбец 3 | |
|---|---|---|---|
| Строка 1 | 5 | 3 | 2 |
| Строка 2 | 4 | 6 | 9 |
| Строка 3 | 7 | 8 | 1 |
В данной матрице элементом 7 является седловой точкой, так как он является максимумом в строке 3 и минимумом в столбце 1.
Седловая точка матрицы: свойства
1. Уникальность в столбце и строке. Седловая точка имеет наибольшее значение в своем столбце и наименьшее значение в своей строке. Это означает, что нет других элементов матрицы, которые бы были больше седловой точки в столбце или меньше в строке.
2. Отсутствие нескольких седловых точек. Матрица может иметь только одну седловую точку или не иметь ее вообще. Это означает, что в столбце может быть только один наибольший элемент, который является седловой точкой, и в строке может быть только один наименьший элемент, который также является седловой точкой.
3. Возможность отсутствия седловой точки. Не все матрицы имеют седловые точки. В некоторых случаях может быть так, что нет элементов, удовлетворяющих условиям седловой точки.
4. Возможность наличия нескольких седловых точек. Некоторые матрицы могут содержать несколько седловых точек, если в одной строке или столбце имеются несколько наименьших или наибольших элементов, соответственно.
Знание этих свойств поможет вам понять, как распознать и определить седловые точки в матрице.
Примеры седловых точек матриц
Матрица 2x2:
2 1 3 4
В данном примере точка (2) является седловой точкой матрицы. Она является наименьшим элементом в своей строке (2 1).
Матрица 3x3:
4 9 1 2 6 5 3 8 7
В данном примере точка (6) является седловой точкой матрицы. Она является наименьшим элементом в своей строке (6 2).
Матрица 4x4:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
В данном примере точка (13) является седловой точкой матрицы. Она является наименьшим элементом в своей строке (13 9).
Таким образом, седловые точки матриц могут быть найдены в различных размерностях матрицы и представляют собой элементы, которые выделяются по своим значениям в строке и столбце.
Применение седловых точек в математике и науке
Одно из основных применений седловых точек - это в экономике. В экономической теории седловая точка матрицы используется для определения равновесия в экономической системе. Это позволяет найти оптимальные значения переменных для достижения максимального прибытка или минимальных затрат.
Другое применение седловых точек связано с игрой теорией. В теории игр седловые точки используются для анализа стратегий и нахождения оптимальных решений в игре между двумя или более игроками. Седловая точка определяет равновесие, при котором ни одному игроку нет смысла менять свою стратегию, так как он не может улучшить свое положение, играя против оптимальной стратегии противника.
Седловые точки также применяются в оптимизации и линейном программировании. Они помогают найти оптимальное решение для системы ограничений. Благодаря своим особенностям, седловые точки приносят большую пользу в решении задачи максимизации или минимизации.
В области искусственного интеллекта и машинного обучения седловые точки используются для оптимизации алгоритмов и моделей. Они помогают найти оптимальные значения параметров и сделать прогнозы на основе имеющихся данных.
Использование седловых точек распространено и в других областях, таких как физика, биология, социология и др. Они позволяют анализировать сложные системы и находить оптимальные решения для достижения желаемых результатов.








