Векторы являются важным понятием в области математики и физики. Они представляют собой стрелки, которые указывают на направление и величину величины или вектора. Один из интересных типов векторов - противоположно направленные векторы.
Противоположно направленные векторы - это пары векторов, которые указывают в противоположных направлениях. Они имеют одинаковую величину, но противоположные знаки. Например, если один вектор указывает направо, то противоположно направленный вектор будет указывать налево.
Противоположно направленные векторы можно представить с помощью математического обозначения. Вектор A и вектор -A считаются противоположно направленными. Они имеют одинаковую величину, но разные знаки. Например, если вектор A имеет координаты (3, -4), то вектор -A будет иметь координаты (-3, 4).
Примером противоположно направленных векторов может служить вектор силы и силы противодействия. Если вектор силы указывает налево, то вектор силы противодействия будет направлен вправо. Оба вектора будут иметь одинаковую величину, но противоположные знаки.
Противоположно направленные векторы имеют важное значение в различных областях, таких как физика, геометрия и информатика. Изучение этих векторов помогает понять принципы силы и противодействия, а также позволяет решать различные математические задачи.
Векторы и их определение
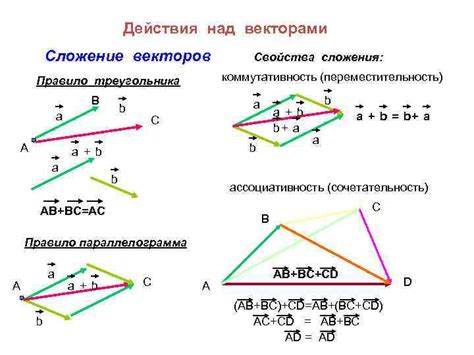
Определение вектора включает две основные характеристики: модуль (величину) и направление. Модуль вектора - это его числовое значение и обозначается числом. Направление вектора - это прямая, на которой лежит вектор, или угол с положительным направлением оси координат. Направление вектора может задаваться числом или с использованием направления на некоторый предмет или место.
Обычно векторы обозначаются строчными буквами с векторным значком над ними, например, вектор силы обозначается как F. Также векторы могут быть представлены в виде стрелок, где длина стрелки соответствует модулю вектора, а направление стрелки - его направлению.
| Примеры векторов | Описание |
|---|---|
| Вектор скорости | Характеризует скорость движения объекта и имеет модуль (величину) и направление. |
| Вектор ускорения | Описывает изменение скорости объекта и также имеет модуль и направление. |
| Вектор силы | Характеризует воздействие на объект и имеет модуль и направление. |
Определение и понимание векторов является важным в различных областях науки и инженерии, таких как физика, математика, геометрия, аэродинамика и др. Понимание противоположно направленных векторов позволяет анализировать различные взаимодействия и движения объектов в пространстве.
Противоположно направленные векторы: основные понятия
Одно из основных понятий, связанных с противоположно направленными векторами, - это векторное сложение. При сложении двух векторов противоположного направления и одинакового по модулю, сумма векторов равна нулевому вектору. Это означает, что противоположно направленные векторы могут компенсировать друг друга.
Примером противоположно направленных векторов может служить сила тяжести и противовес, действующие на тело. Сила тяжести направлена вниз, а противовес - вверх. Оба вектора имеют одинаковую величину (модуль), но противоположное направление. Их сумма равна нулевому вектору, что означает, что на тело не будет действовать никакая сила.
Противоположно направленные векторы также применяются для описания движения тела в противоположных направлениях. Например, при движении автомобиля вперед и взгляде назад, оба вектора имеют одинаковую величину (скорость), но противоположное направление.
Определение противоположно направленных векторов

Противоположно направленные векторы обозначаются знаком "-" перед вектором. Например, если вектор A направлен вправо, то противоположно направленный вектор будет обозначаться как -A и будет указывать влево.
Противоположно направленные векторы часто используются в физике для описания движения тел и сил. Например, если два тела движутся навстречу друг другу с одинаковой скоростью, то их скорости будут противоположно направленными векторами.
Что такое противоположно направленные векторы?
Математически, два вектора a и b называются противоположно направленными, если их сумма равна нулевому вектору. Иными словами, если a + b = 0, то векторы a и b являются противоположно направленными.
Примером противоположно направленных векторов может служить движение тела в противоположных направлениях. Например, если одно тело движется влево, а другое тело движется вправо с одинаковой скоростью, то векторы скорости этих двух тел будут противоположно направленными, так как указывают в противоположные стороны.
Примеры противоположно направленных векторов
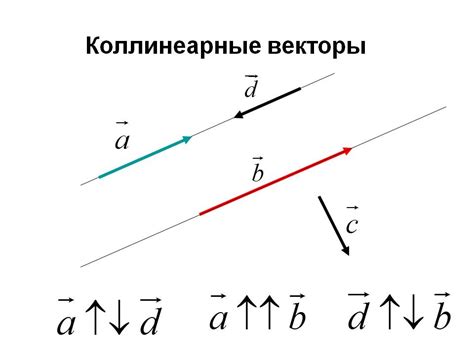
Ниже представлены несколько примеров противоположно направленных векторов:
1. Движение поезда: Если поезд движется вперед, то вектор его движения направлен вперед, а противоположный вектор будет указывать в обратную сторону, то есть назад.
2. Тяготение: Вектор тяготения, действующий на объект падающий вниз, будет направлен вниз, а противоположно направленный вектор будет указывать вверх.
3. Сила трения: Если объект движется вперед, сила трения, действующая против движения, будет направлена назад, а противоположно направленная сила трения будет указывать вперед.
Во всех этих примерах направления векторов являются противоположными друг другу.
Пример противоположно направленных векторов в физике
В физике есть множество примеров противоположно направленных векторов. Рассмотрим несколько из них:
- Скорость: если два тела движутся в разных направлениях, их скорости считаются противоположно направленными векторами. Например, если одно тело движется вправо со скоростью 10 м/с, а другое движется влево со скоростью 10 м/с, то их векторы скорости будут противоположно направленными.
- Сила: если две силы действуют в противоположных направлениях на одно и то же тело, то их векторы считаются противоположно направленными. Например, если сила тяготения действует вниз, а сила подъема действует вверх на один и тот же объект, то их векторы сил будут противоположно направленными.
- Ускорение: если движущееся тело замедляется или изменяет направление движения, его ускорение может считаться противоположно направленным вектором. Например, если автомобиль едет на запад со скоростью 20 м/с и его скорость начинает уменьшаться, то его ускорение будет направлено на восток и будет противоположно направленным вектором.
Это лишь некоторые примеры противоположно направленных векторов в физике. Изучение и понимание их играют важную роль в различных областях науки и техники.
Пример противоположно направленных векторов в математике
Рассмотрим пример: движение по прямой. Пусть у нас есть вектор "a", который описывает движение вправо на 5 единиц. Также у нас есть вектор "b", который описывает движение влево на 5 единиц. В этом случае вектор "a" и вектор "b" являются противоположно направленными векторами, так как они направлены в противоположные стороны, но имеют одинаковые по модулю значения.
Математически, это может быть представлено следующим образом:
a = 5
b = -5
Где "-" перед числом "5" указывает на противоположное направление.
Примеры противоположно направленных векторов также могут быть найдены в других областях, например, в физике и геометрии. Важно понимать, что противоположно направленные векторы имеют разные знаки, но одинаковые по модулю значения, что делает их противоположными по направлению, но равными по величине.
Свойства противоположно направленных векторов
Вот некоторые свойства противоположно направленных векторов:
| Сложение | Сумма двух противоположно направленных векторов всегда будет равна нулевому вектору. Это свойство можно выразить следующим образом: |
В + (-В) = 0 | |
| Умножение на число | Умножение противоположно направленного вектора на любое число приведет к получению противоположно направленного вектора с измененной длиной, но сохраненным направлением. Это свойство можно выразить следующим образом: |
-В * а = -(В * а) = (-В) * а (где а - любое число) | |
| Параллельность | Противоположно направленные векторы всегда параллельны друг другу. Это означает, что они лежат на одной прямой. |
| Равенство | Два противоположно направленных вектора считаются равными, если они имеют одинаковую длину и противоположные направления. |
Применение знания о свойствах противоположно направленных векторов может быть полезно при выполнении различных математических и физических задач, таких как нахождение силы трения или решение уравнений с противоположно направленными векторами.
Сложение и вычитание противоположно направленных векторов
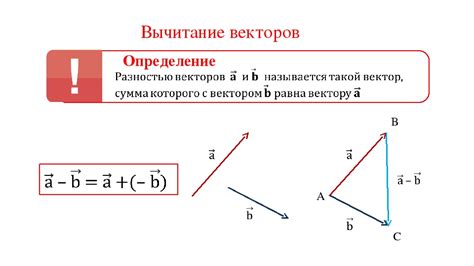
Противоположно направленные векторы имеют разные направления, но одинаковые по величине. Для сложения противоположно направленных векторов достаточно их отнять друг от друга.
Допустим, у нас есть вектор a, направленный вправо, и вектор -a, направленный влево. Векторы a и -a являются противоположно направленными.
Сложение противоположно направленных векторов происходит путем вычитания их компонент. Если a = (a1, a2) и -a = (-a1, -a2), то их сумма равна (a1 - (-a1), a2 - (-a2)). Упрощая выражение, получаем (a1 + a1, a2 + a2), что равно (2a1, 2a2).
Вычитание противоположно направленных векторов также происходит путем сложения их компонент. Если a = (a1, a2) и -a = (-a1, -a2), то их разность равна (a1 + (-a1), a2 + (-a2)). Упрощая выражение, получаем (0, 0), что является нулевым вектором.
Пример:
- Пусть a = (3, 2) и -a = (-3, -2). Сумма противоположно направленных векторов равна (3 - (-3), 2 - (-2)) = (6, 4).
- Пусть b = (-5, -7) и -b = (5, 7). Разность противоположно направленных векторов равна (-5 + 5, -7 + 7) = (0, 0).
Скалярное произведение противоположно направленных векторов
Если два вектора являются противоположно направленными, то их скалярное произведение будет отрицательным. Пусть у нас есть два вектора v и w, противоположно направленные друг другу. Их скалярное произведение можно записать следующим образом:
v ⋅ w = |v| ⋅ |w| ⋅ cos(180°) = - |v| ⋅ |w|,
где |v| и |w| - длины векторов v и w соответственно.
Таким образом, если векторы v и w являются противоположно направленными, скалярное произведение между ними будет равно отрицательному числу, умноженному на произведение их длин. Например, если |v| = 3 и |w| = 4, то v ⋅ w = -12.








