Приближение функций - это изучение и использование методов, которые помогают аппроксимировать сложные функции более простыми или более понятными. Это важная область математики и её применений, и использование этих методов может быть полезно во многих научных и инженерных задачах.
В данной статье мы рассмотрим несколько простых способов приближения функций. Один из них - это линейная аппроксимация. Этот метод основан на приближении функции линейной функцией (прямой линией). Хотя такое приближение может быть грубым, оно может быть достаточно точным в некоторых случаях.
Другим методом приближения функций является полиномиальная аппроксимация. В этом методе функция приближается полиномом определенной степени. Чем выше степень полинома, тем более точным будет приближение. Однако использование полиномиальной аппроксимации может быть затруднено из-за сложности вычислений и необходимости знания точного значения функции в нескольких точках.
Также существует ещё один метод - интерполяция. При интерполяции используется набор заданных точек для построения гладкой функции, проходящей через эти точки. Это может быть полезно, когда известны только конкретные значения функции в определенных точках и требуется получить приближение для других значений.
Важно помнить, что каждый метод имеет свои преимущества и ограничения, и выбор метода зависит от конкретной задачи и требуемой точности приближения. Важно также учитывать, что приближение функций может быть полезно не только с математической точки зрения, но и в практических приложениях для решения различных задач.
Математическое определение и основные понятия

Функция обычно обозначается символом f(x), где f – это имя функции, а x – переменная, от которой зависит функция. Значение функции f(x) в точке x обозначается как f(x).
График функции – это геометрическое представление функции в координатной плоскости. График функции является множеством всех упорядоченных пар (x, f(x)), где x принадлежит области определения функции.
Функция может быть задана явно, когда правило, по которому определены значения функции, представлено в виде аналитической формулы или выражения. Например, f(x) = x^2.
Также функцию можно задать неявно, когда значение функции определяется как решение уравнения или системы уравнений. Например, уравнение окружности x^2 + y^2 = r^2 задает зависимость y от x, и можно сказать, что y является функцией от x в этом случае.
Функции могут быть линейными, квадратичными, тригонометрическими, экспоненциальными и другими видами функций, которые описывают различные зависимости в природе и науке.
Аппроксимация: что это и зачем нужно?
Аппроксимация широко применяется в научных и инженерных расчетах, а также в статистике, для упрощения и анализа сложных данных. Использование аппроксимации помогает ускорить вычисления, упростить математические модели и сделать интерпретацию данных более понятной.
Основная цель аппроксимации - найти более простую функцию или модель, которая приближенно описывает исходные данные или функцию. При этом, чем меньше ошибка аппроксимации, тем более точно новая функция или модель описывает исходные данные.
Существует множество методов аппроксимации, включая интерполяцию, приближение полиномами, сглаживание данных и другие. Выбор оптимального метода зависит от характера исходных данных, требуемой точности и других факторов. Некоторые из этих методов используют математические алгоритмы, а другие основаны на статистических методах.
| Преимущества аппроксимации | Недостатки аппроксимации |
|---|---|
| Упрощение сложных данных или функций | Потеря точности |
| Ускорение вычислений | Возможность пропустить значимую информацию |
| Улучшение интерпретации данных | Зависимость от выбранного метода аппроксимации |
В заключение, аппроксимация - это мощный инструмент в области анализа данных и численных расчетов. Она помогает упростить сложные функции и данные, ускорить вычисления, улучшить интерпретацию данных. Однако, при использовании аппроксимации необходимо учитывать возможные потери точности и зависимость результатов от выбранного метода аппроксимации.
Линейная аппроксимация и ее особенности
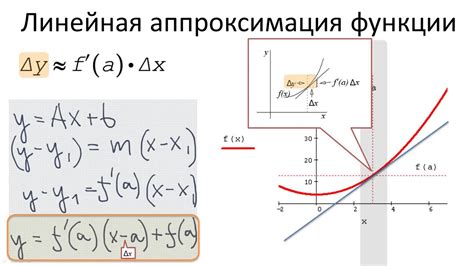
Для выполнения линейной аппроксимации необходимо иметь две точки на графике функции. Пара значений (x1, y1) и (x2, y2) позволяет определить уравнение прямой y = kx + b, которая будет наилучшим образом приближать исходную функцию на отрезке [x1, x2].
Коэффициенты k и b находятся из системы уравнений:
y1 = k * x1 + b
y2 = k * x2 + b
Решение данной системы позволяет определить значения k и b, которые представляют собой угловой коэффициент и свободный член уравнения прямой соответственно.
Одним из главных преимуществ линейной аппроксимации является ее простота. Она не требует использования сложных математических методов и алгоритмов. Кроме того, линейная аппроксимация актуальна в случаях, когда аппроксимируемая функция достаточно близка к прямой линии на заданном отрезке.
Однако, следует заметить, что линейная аппроксимация имеет свои ограничения. Если исходная функция имеет существенные отклонения от прямой на заданном отрезке, то линейная аппроксимация может давать неточные результаты. В таких случаях необходимо использовать более сложные методы или увеличивать количество точек для аппроксимации.
Полиномиальная аппроксимация: преимущества и недостатки
Однако полиномиальная аппроксимация имеет свои недостатки. Во-первых, она может быть ограничена в точности. Полиномиальная функция может приблизить исходную функцию только в определенном диапазоне значений, и за пределами этого диапазона может происходить существенное отклонение. Во-вторых, использование полиномов высокой степени может привести к проблемам численной неустойчивости. Например, частые сложения и умножения больших чисел могут привести к большим ошибкам округления и ошибкам вычислений.
Кроме того, приближение полиномиальной функцией может потребовать большого количества коэффициентов, особенно для сложных функций. Это может усложнить анализ и интерпретацию полученных результатов. Кроме того, полиномиальная аппроксимация может быть времязатратной операцией, особенно для функций с большим количеством точек данных.
В целом, полиномиальная аппроксимация является мощным инструментом для приближения функций, но требует внимательного подхода и оценки ее ограничений и недостатков.
Аппроксимация с помощью интерполяции
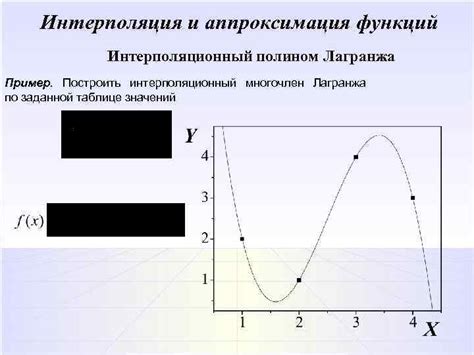
Интерполяцию можно выполнять разными способами, но наиболее распространенными являются методы наименьших квадратов и использование полиномиальной интерполяции. При использовании метода наименьших квадратов строится функция, которая наилучшим образом соответствует заданным значениям функции. Полиномиальная интерполяция основывается на построении полинома, проходящего через известные точки функции.
Для выполнения интерполяции можно использовать различные алгоритмы, такие как метод Ньютона, метод Лагранжа или метод Эрмита. Каждый из этих алгоритмов имеет свои особенности и преимущества, поэтому выбор конкретного алгоритма зависит от требуемой точности и удобства использования.
| Преимущества интерполяции | Недостатки интерполяции |
|---|---|
| - Простота в использовании. | - Возможность появления огромных колебаний в окрестности точек интерполяции. |
| - Возможность достаточно точного приближения функции. | - Возможность увеличения ошибки при использовании полиномов больших степеней. |
| - Возможность получения значений функции в произвольных точках. | - Возможность плохой интерполяции, если значения функции сильно отличаются в заданных точках. |
Итак, интерполяция представляет собой удобный и эффективный способ приближения функции, который может быть использован в различных областях науки и техники. Однако следует помнить о ее ограничениях и возможных недостатках, и выбирать оптимальный метод интерполяции, учитывая конкретную задачу.
Аппроксимация с использованием метода наименьших квадратов
Для аппроксимации функции с использованием метода наименьших квадратов необходимо иметь набор данных, состоящий из x-координат и соответствующих им y-координат. Задача состоит в нахождении функции, которая минимизирует расстояние между значениями y-координат и значениями функции.
Алгоритм работы метода наименьших квадратов следующий:
- Выбрать приближающую функцию. Это может быть линейная функция, полиномиальная функция или другой вид функции, в зависимости от предполагаемого вида зависимости данных.
- Подобрать коэффициенты приближающей функции таким образом, чтобы минимизировать сумму квадратов отклонений между значениями y-координат и значениями функции.
- Оценить качество аппроксимации с использованием различных метрик, таких как средняя квадратичная ошибка или коэффициент детерминации.
Метод наименьших квадратов широко используется в различных областях, включая физику, экономику, статистику и машинное обучение. Он позволяет находить аналитическое выражение для функции, которая наилучшим образом приближает экспериментальные данные, и использовать это выражение для проведения различных анализов и прогнозирования значений функции для новых наборов данных.
Кусочно-постоянная аппроксимация
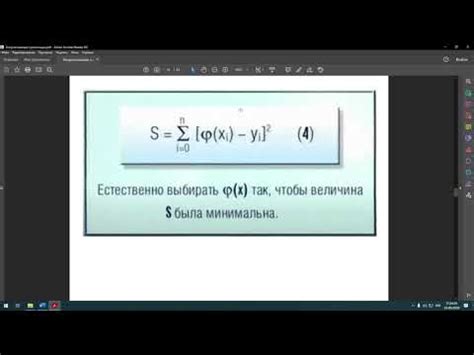
Для приближения функции кусочно-постоянной функцией необходимо разбить отрезок, на котором задана функция, на несколько подотрезков. Затем на каждом подотрезке необходимо выбрать постоянное значение функции так, чтобы оно наилучшим образом приближало исходную функцию.
Кусочно-постоянная аппроксимация широко используется в математике, физике и инженерии. Этот метод позволяет упростить вычисления и анализ функций, а также улучшить понимание свойств исследуемого явления.
Преимущества кусочное постоянной аппроксимации включает простоту вычислений и возможность аналитического исследования полученной кусочно-постоянной функции. Кусочно-постоянная аппроксимация также может быть использована для аппроксимации кривых и поверхностей в трехмерном пространстве.
Однако, кусочно-постоянная аппроксимация имеет свои недостатки. Она может привести к потере точности приближения функции, особенно при большом количестве подотрезков. Кроме того, кусочно-постоянная аппроксимация может быть неадекватной для функций с быстрыми изменениями и осцилляциями.
В целом, кусочно-постоянная аппроксимация - это удобный и эффективный способ приближения функции во многих областях науки и техники. Он позволяет упростить сложные математические задачи, а также улучшить понимание и анализ исследуемого явления.
Аппроксимация с помощью граничных условий
Один из способов приблизить функцию состоит в использовании граничных условий, которые определяют значения функции на границе определенного интервала.
Для аппроксимации функции с помощью граничных условий можно использовать различные методы, такие как метод конечных разностей или метод конечных элементов.
Метод конечных разностей основан на аппроксимации производных функции с помощью разностных формул. Граничные условия используются для определения значений функции на границе интервала. Затем, решая систему уравнений, полученную с использованием разностной аппроксимации, можно получить приближенное решение задачи.
Метод конечных элементов также использует граничные условия, но представление функции осуществляется с помощью базисных функций, определенных на конечных элементах. Значения функции на границе интервала определяются с помощью граничных условий. Затем, решая систему уравнений, полученную с использованием метода конечных элементов, можно получить приближенное решение задачи.
Аппроксимация с помощью граничных условий является одним из важных методов для решения задач математической физики и инженерных задач. Он позволяет получить приближенное решение функции на заданном интервале с заданной точностью.
Однако следует учитывать, что аппроксимация с помощью граничных условий может давать только приближенное решение и не всегда достаточно точное. Для более точного аппроксимации функции могут потребоваться более сложные методы и моделирование с использованием компьютерных программ.
Аппроксимация с помощью сплайнов
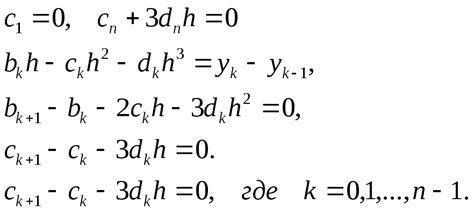
Преимуществом аппроксимации с помощью сплайнов является то, что она позволяет создать кривую, которая адаптируется к заданным точкам и сохраняет гладкость функции. Это полезно, когда необходимо приблизить функцию, имеющую разрывы или резкие изменения.
Существует несколько видов сплайнов, таких как линейные, квадратичные или кубические сплайны, в зависимости от степени полиномов, составляющих сплайн. Кубические сплайны наиболее часто используются, так как они обеспечивают наилучшую аппроксимацию и гладкость функции.
Процесс создания сплайна состоит из нескольких шагов:
- Интерполяция: нахождение интерполяционного полинома для каждого отрезка между заданными точками.
- Нахождение коэффициентов: определение коэффициентов полинома для каждого отрезка путем решения системы уравнений.
- Соединение отрезков: объединение полиномов для каждого отрезка, чтобы образовать сплайн.
Таким образом, аппроксимация с использованием сплайнов позволяет достичь гладкости и точности приближения функции. Этот метод широко применяется в различных областях, таких как компьютерная графика, численное моделирование, статистика и машинное обучение.
Примеры применения аппроксимации в реальной жизни
1. Физика
В физике аппроксимация широко используется для приближения зависимостей между физическими величинами. Например, при моделировании движения тела под действием силы трения или сопротивления воздуха, можно использовать аппроксимацию для приближенного описания траектории движения.
2. Экономика
Аппроксимация применяется в экономических исследованиях для анализа и приближения экономических зависимостей, например, спроса и предложения на рынке или зависимости дохода от образования и опыта работы.
3. Инженерия
В инженерии аппроксимация используется при проектировании и моделировании различных систем и процессов. Например, при проектировании аэродинамических профилей крыла самолета, можно использовать аппроксимацию для приближенного расчета аэродинамических характеристик и оптимизации дизайна.
4. Медицина
В медицине аппроксимация может использоваться для анализа результатов исследований или наблюдений, приближенного моделирования физиологических процессов или прогнозирования заболеваемости и эффективности лечения.
5. Финансы
Аппроксимация часто применяется в финансовой аналитике и оценке рыночных рисков. Например, для оценки цены активов или прибыли можно использовать аппроксимацию для приближенного моделирования финансовых рынков и прогнозирования их будущего поведения.
Применение аппроксимации в реальной жизни позволяет упростить анализ и моделирование сложных функций, а также получить приближенные результаты, которые могут быть полезны в принятии решений и планировании различных процессов и явлений.








