Одной из важнейших задач в математике является нахождение суммы бесконечного ряда. Для этого необходимо установить заданную точность, чтобы приближенное значение равнялось реальному с нужной точностью. В этой статье мы рассмотрим несколько способов, которые позволят вам посчитать сумму ряда с заданной точностью.
Один из способов нахождения суммы ряда с заданной точностью - это использование численных методов, таких как метод Монте-Карло или метод трапеций. Эти методы позволяют аппроксимировать сумму ряда путем приближенного вычисления интегралов или использования случайных чисел. Однако, такие методы требуют определенных вычислительных ресурсов и могут быть неэффективными для сложных рядов.
Другим способом является использование аналитического метода, который позволяет найти точное значение суммы ряда. При этом необходимо разложить ряд в более простую форму, например, в виде сходящегося ряда или интеграла. Затем, используя свойства ряда и алгебраические преобразования, можно получить точное значение суммы ряда.
Например, таким образом можно вычислить значение числа e (основание натурального логарифма) с заданной точностью: разложив его в бесконечный ряд e = 1 + 1/1! + 1/2! + 1/3! + ..., можно остановить вычисление суммы в тот момент, когда разница между приближенным значением и точным значением будет меньше заданной точности.
Таким образом, нахождение суммы ряда с заданной точностью может быть достигнуто различными способами, в зависимости от сложности ряда и требуемой точности. Важно учитывать, что для сложных рядов может потребоваться больше ресурсов и времени для вычисления точного значения.
Методы подсчета суммы ряда с заданной точностью: основные приемы и советы

1. Метод последовательного приближения. Этот метод заключается в последовательном приближении к требуемой точности суммы ряда путем сложения определенного числа слагаемых. Для этого необходимо определить условие остановки, то есть задать требуемую точность. Затем, в цикле, суммируются слагаемые ряда до тех пор, пока не достигнута заданная точность.
2. Метод суммирования по диапазону. Этот метод предполагает разбиение ряда на диапазоны и суммирование слагаемых в каждом диапазоне. Затем полученные суммы складываются. Чтобы достичь требуемой точности, можно изменять размеры диапазонов и сравнивать результаты с предыдущими. Если разность между результатами достаточно маленькая, можно считать, что требуемая точность достигнута.
3. Метод ряда Тейлора. Этот метод используется для вычисления функций с помощью ряда. Ряд Тейлора представляет функцию в виде суммы бесконечного ряда слагаемых. Путем последовательного приближения к требуемой точности суммы ряда можно вычислить значение функции. Для этого необходимо ограничить число слагаемых в ряду, итеративно увеличивая его до достижения заданной точности.
4. Метод использования алгоритмов численного анализа. Существует множество алгоритмов численного анализа, которые позволяют найти численное значение суммы ряда с заданной точностью. Некоторые из этих алгоритмов включают методы численного интегрирования, численного дифференцирования, интерполяции и другие.
При использовании любого из указанных методов важно осознать, что точность результата зависит от точности входных данных и выбранного алгоритма. Необходимо быть внимательным при выборе метода и правильно настроить параметры для достижения требуемой точности. Также рекомендуется проверять результаты с помощью других методов или аналитических решений, чтобы убедиться в правильности полученной суммы ряда.
Арифметический подход к решению задачи
Для начала, мы можем выразить каждый элемент ряда через его предыдущий элемент и коэффициент убывания:
$$a_n = q \cdot a_{n-1}$$
где $$a_n$$ - n-ый элемент ряда, $$a_{n-1}$$ - (n-1)-ый элемент ряда, а q - коэффициент убывания.
Затем, мы можем записать искомую сумму ряда как:
$$S = a_1 + a_2 + a_3 + ... + a_n$$
Проанализировав данную сумму, мы можем заметить, что множество элементов ряда сокращается, и остаются только отдельные элементы, образующие геометрическую прогрессию:
$$S = a_1 + q \cdot a_1 + q^2 \cdot a_1 + ... + q^{n-1} \cdot a_1$$
Заметим, что данная сумма представляет собой сумму геометрической прогрессии с первым элементом $$a_1$$ и знаменателем q.
Таким образом, для нахождения суммы ряда с заданной точностью, мы можем использовать формулу суммы геометрической прогрессии:
$$S = \frac{a_1 \cdot (1 - q^n)}{1 - q}$$
где $$a_1$$ - первый элемент ряда, q - коэффициент убывания, n - количество слагаемых суммы.
Этот подход позволяет получить результат суммы ряда с заданной точностью, минимизируя количество операций. Однако, следует учитывать особенности каждой конкретной задачи и правильно выбирать коэффициент убывания и первый элемент ряда для достижения необходимой точности.
Геометрические прогрессии как основа для вычислений

Геометрическая прогрессия представляет собой последовательность чисел, в которой каждый последующий элемент получается умножением предыдущего элемента на фиксированный множитель. Данная прогрессия имеет важное применение в вычислениях, включая подсчет суммы ряда с заданной точностью.
Формула расчета суммы геометрической прогрессии выглядит следующим образом:
Sn = a1 * (1 - qn) / (1 - q),
где:
- Sn - сумма первых n членов прогрессии;
- a1 - первый член прогрессии;
- q - множитель прогрессии;
- n - количество членов прогрессии.
Для вычисления суммы ряда с заданной точностью необходимо сравнить значение очередного элемента прогрессии с требуемой точностью и прекратить итерации, когда значение станет меньше этой точности.
Пример использования геометрической прогрессии в вычислениях можно представить при подсчете суммы бесконечного ряда, такого как ряд Гейзеля:
S = a / (1 - q),
где:
- S - сумма бесконечного ряда;
- a - первый член ряда;
- q - множитель ряда (|q| < 1).
Геометрические прогрессии являются эффективным инструментом для вычислений сумм рядов с заданной точностью, что позволяет сократить количество итераций и улучшить скорость выполнения расчетов.
Точность в математике: погрешности и их учет при расчетах
Существуют различные виды погрешностей, включая абсолютную погрешность и относительную погрешность. Абсолютная погрешность - это абсолютное значение разницы между истинным и приближенным значением, а относительная погрешность - отношение абсолютной погрешности к истинному значению.
При выполнении расчетов с заданной точностью необходимо учитывать погрешности, чтобы получить достоверные результаты. Для этого можно использовать различные методы и алгоритмы, такие как метод Ньютона или метод простой итерации.
Один из способов учета погрешностей - это установка предельного значения для разности между двумя последовательными значениями ряда. Если разность меньше или равна заданному предельному значению, расчеты считаются достаточно точными и могут быть остановлены.
Важно также учесть, что точность расчетов может быть улучшена путем увеличения количества итераций или изменения алгоритма расчетов. Однако необходимо оценивать затраты на вычисления и решать, насколько точные результаты требуются.
При выполнении численных расчетов важно помнить о погрешностях и учитывать их в процессе расчетов. Это поможет получить более достоверные результаты и избежать неправильных выводов.
Примеры суммирования рядов с использованием разных методов
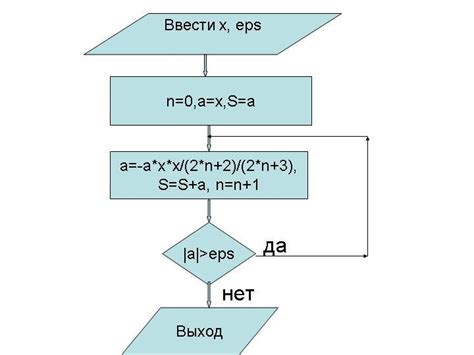
Метод простых последовательных слагаемых
В качестве примера рассмотрим ряд:
1 + 1/2 + 1/3 + 1/4 + 1/5 + ...
Сумма первых n слагаемых этого ряда может быть вычислена следующим образом:
s_n = 1 + 1/2 + 1/3 + ... + 1/n
При достаточно большом значении n можно получить приближенное значение суммы ряда с требуемой точностью.
Метод частичной суммы ряда
Для примера используем ряд:
1 - 1/2 + 1/3 - 1/4 + ...
Сумма первых n слагаемых этого ряда может быть записана как:
s_n = 1 - 1/2 + 1/3 - ... + (-1)^(n+1)/n
Вычисление значения суммы с помощью этого метода требует выполнения большого числа арифметических операций, но при достаточно большом значении n можно получить приближенное значение суммы с заданной точностью.
Метод взвешенного среднего
Для примера рассмотрим ряд:
1/2 + 1/4 + 1/8 + ...
Сумма первых n слагаемых этого ряда может быть записана как:
s_n = 1/2 + 1/4 + ... + 1/2^n
С помощью метода взвешенного среднего можно получить приближенное значение суммы ряда с заданной точностью путем усреднения найденных значений сумм с различными значениями n.
Советы по оптимизации вычислений для повышения скорости работы программы
При работе с вычислительными задачами часто возникает необходимость оптимизировать программу для повышения скорости ее работы. Ниже представлены некоторые советы по оптимизации вычислений:
- Используйте эффективные алгоритмы: Перед началом работы над программой проанализируйте возможные алгоритмы решения задачи и выберите наиболее оптимальный вариант. Некоторые алгоритмы могут иметь более высокую сложность, чем другие, поэтому выбор правильного алгоритма может существенно повлиять на скорость работы программы.
- Избегайте повторных вычислений: Если в вашем коде есть части, которые выполняются несколько раз, то попытайтесь избегать повторных вычислений этих частей. Используйте переменные для сохранения уже вычисленных значений и повторно используйте их вместо повторного выполнения вычислений.
- Используйте подходящие типы данных: При работе с числами выбирайте подходящие типы данных для хранения и обработки значений. Использование более компактных типов данных может сократить объем используемой памяти и повысить скорость операций.
- Минимизируйте операции внутри циклов: Если внутри цикла есть операции, которые не зависят от его переменных, то переместите их за пределы цикла. Это поможет сократить время выполнения цикла и увеличить общую скорость программы.
- Используйте параллельные вычисления: Если вашей задаче требуется обработка большого объема данных, то попробуйте использовать параллельные вычисления. Распараллеливание задачи может помочь ускорить работу программы путем распределения вычислений между несколькими ядрами процессора или между несколькими компьютерами.
- Удаляйте неиспользуемый код: Проверьте вашу программу на наличие неиспользуемого кода или неиспользуемых переменных. Избавление от неиспользуемого кода может существенно сократить время выполнения программы.
- Используйте специализированные библиотеки: Если вам требуется выполнить сложные математические вычисления, то попробуйте использовать специализированные библиотеки для таких вычислений. Они часто имеют оптимизированный код, который может существенно ускорить выполнение вычислений.
Следуя этим советам, вы сможете оптимизировать программу и повысить скорость ее работы. Однако, необходимо помнить, что оптимизация может снизить читаемость и поддерживаемость кода, поэтому не забывайте о балансе между скоростью работы программы и ее качеством.








