Ортонормированный базис - это набор векторов, удовлетворяющих двум важным условиям: они ортогональны (перпендикулярны) друг другу, их нормы равны единице. Такой базис является одним из ключевых понятий в линейной алгебре и находит широкое применение в различных областях науки и техники.
Ортонормированный базис часто используется для удобства векторного представления данных. Он позволяет разложить любой вектор на независимые составляющие, обозначаемые координатами по каждому из базисных векторов. Так, каждый вектор представляется в виде суммы произведений его координат на соответствующие базисные векторы.
Примером ортонормированного базиса является стандартный базис в трехмерном пространстве, состоящий из векторов i, j и k. Координаты этих векторов соответственно равны [1, 0, 0], [0, 1, 0] и [0, 0, 1]. Определив длину каждого из базисных векторов равной единице, мы получаем ортонормированный базис.
Ортонормированные базисы также играют важную роль в решении уравнений, представленных в матричной форме. Они позволяют упростить эти уравнения и получить более наглядные и понятные решения. Матричные операции, такие как умножение матрицы на вектор или на другую матрицу, легче выполнять в ортонормированном базисе, что позволяет существенно сократить время вычислений.
Определение ортонормированного базиса

Ортонормированный базис играет важную роль в линейной алгебре и математическом анализе. Он позволяет представлять любой вектор в данном векторном пространстве как линейную комбинацию его базисных векторов. Такое представление удобно для решения различных задач, включая вычисление координат вектора, ортогональные и параллельные преобразования, ортогональные проекции, скалярные произведения и многое другое.
Примеры ортонормированных базисов:
- Канонический базис в трехмерном пространстве: {(1, 0, 0), (0, 1, 0), (0, 0, 1)}
- Базис Фурье в пространстве функций: {1, cos(x), sin(x)}
- Базис Хаара в пространстве сигналов: {1, h1(x), h2(x), ..., hn(x)}
Ортонормированный базис является важным инструментом для различных областей математики и физики, так как он позволяет удобно и эффективно описывать и анализировать структуру векторных пространств и их свойства.
Примеры ортонормированных базисов
1. Стандартный базис в трехмерном пространстве: {e1, e2, e3}, где e1 = (1, 0, 0), e2 = (0, 1, 0), e3 = (0, 0, 1). Векторы этого базиса образуют ортонормированную систему, так как их скалярное произведение равно нулю, если векторы различны, и единице, если векторы совпадают. Базис является стандартным, так как его векторы сонаправлены с осями координат.
2. Базис Фурье в пространстве L2[0, 2π] (пространство функций, интегрируемых на отрезке [0, 2π] с квадратом интеграла). Этот базис состоит из тригонометрических функций: {1, cos(x), sin(x)}. Эти функции образуют ортонормированную систему, так как их скалярное произведение равно нулю при различных функциях, и единице при совпадении функций. Базис Фурье широко используется в математическом анализе и обработке сигналов.
3. Канонический базис в пространстве многочленов степени не выше n: {1, x, x2, ..., xn}. Векторы этого базиса образуют ортонормированную систему относительно определенного скалярного произведения (интеграла от произведения двух многочленов). Канонический базис является удобным инструментом для работы с многочленами и решения задач алгебры.
Разница между ортонормированным и ортогональным базисом
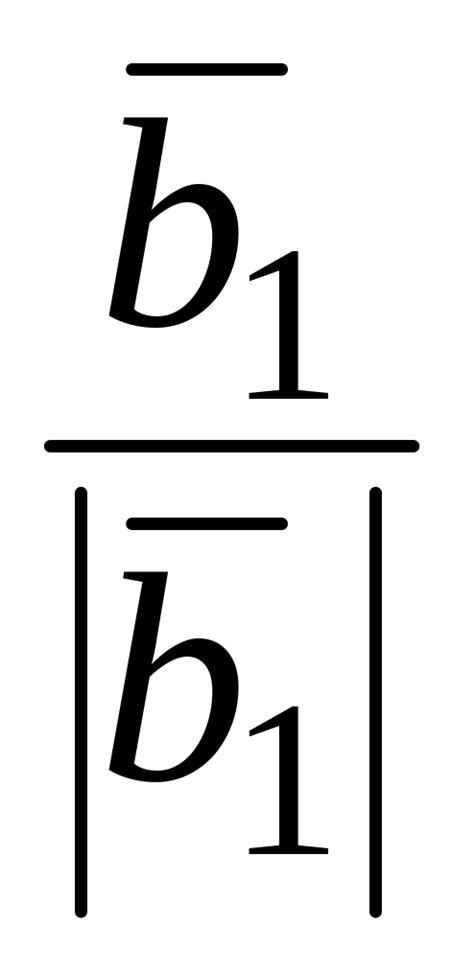
Ортогональный базис - это набор векторов в линейном пространстве, которые попарно ортогональны друг другу. Ортогональные векторы означают, что их скалярное произведение равно нулю. Если векторы ортогонального базиса также нормированы (их длина равна 1), то он становится ортонормированным базисом.
Ортонормированный базис - это более строгое определение, которое требует, чтобы все векторы базиса не только были ортогональными друг другу, но и нормированы между собой. Он образует ортонормированную систему, в которой каждый вектор имеет единичную длину и векторы ортогональны друг другу.
Однако, ортогональный базис не всегда является ортонормированным базисом. Он может содержать векторы, которые ортогональны друг другу, но имеют ненулевую длину, что отличает их от ортонормированного базиса.
Например, в трехмерном пространстве векторы (1, 0, 0), (0, 1, 0) и (0, 0, 1) образуют ортогональный базис, потому что они попарно ортогональны друг другу. Однако, они не являются ортонормированным базисом, так как не нормированы.
Таким образом, основное отличие между ортогональным базисом и ортонормированным базисом заключается в нормировании векторов. Ортогональный базис основывается только на ортогональности, тогда как ортонормированный базис является более строгим определением, требующим и нормирования векторов.
Свойства ортонормированного базиса
1. Ортогональность: В ортонормированном базисе все векторы попарно ортогональны друг другу. Это значит, что скалярное произведение любых двух векторов базиса равно нулю, если векторы не совпадают.
2. Нормализация: Длина каждого вектора ортонормированного базиса равна 1. Это означает, что скалярное произведение вектора базиса на самого себя равно 1.
3. Линейная независимость: Векторы ортонормированного базиса линейно независимы. Это означает, что нельзя линейно выразить один вектор через другие векторы базиса.
4. Удобство в вычислениях: Использование ортонормированного базиса упрощает многие вычисления в линейной алгебре. Например, скалярное произведение векторов в ортонормированном базисе сводится к простому умножению координат векторов.
Пример: Ортонормированный базис в трехмерном пространстве может быть задан векторами {i, j, k}, где i - вектор с началом в начале координат и направленный в положительном направлении оси X, j - вектор в положительном направлении оси Y, и k - вектор в положительном направлении оси Z. В этом базисе каждый вектор имеет длину 1 и ортогонален остальным векторам базиса.








