Поиск экстремумов функции – важный этап в анализе математических моделей и графиков. Независимо от того, занимаетесь ли вы исследованием функции, оптимизацией процессов или прогнозированием результатов, понимание точек экстремума поможет вам принять правильные решения и сделать выводы. В статье мы расскажем, как найти сумму точек экстремума функции и предоставим вам полезные советы и инструкции для надежного и точного анализа функций.
Итак, что такое экстремум функции? И экстремум – это точка на графике функции, в которой функция принимает максимальное или минимальное значение. В зависимости от характера функции, экстремум может быть глобальным или локальным. Глобальный экстремум – это точка, в которой функция принимает наибольшее или наименьшее значение на всей области определения функции. Локальный экстремум – это точка, в которой функция принимает наибольшее или наименьшее значение на небольшом участке области определения функции. Поиск экстремумов производится путем анализа производной функции.
Один из основных инструментов для нахождения точек экстремума функции – анализ первой и второй производной. Первая производная функции позволяет определить области возрастания и убывания функции, а также точки экстремума. Для этого вычисляем производную функции и анализируем знак производной. Если на некотором интервале производная положительна, то функция возрастает. Если на интервале производная отрицательна, то функция убывает. Точки, где производная меняет знак, являются точками экстремума функции.
Анализ функции: простые советы и инструкции

Для проведения анализа функции необходимо выполнить следующие действия:
- Найти область определения функции. Для этого необходимо определить значения, при которых функция имеет смысл.
- Найти точки разрыва функции. Точки разрыва - это значения, при которых функция не определена или не непрерывна.
- Найти точки экстремума функции. Точки экстремума - это значения, при которых функция достигает наибольшего или наименьшего значения.
- Определить интервалы возрастания и убывания функции. Интервалы возрастания - это значения, при которых функция увеличивается. Интервалы убывания - это значения, при которых функция уменьшается.
- Найти асимптоты функции. Асимптоты - это прямые или кривые, к которым функция стремится при приближении к определенным значениям.
Для удобства анализа функции можно использовать таблицу, в которой указываются значения аргумента и значения функции. Это позволяет наглядно представить изменения функции и облегчает нахождение точек экстремума, интервалов возрастания и убывания.
| Аргумент | Значение функции |
|---|---|
| 1 | 5 |
| 2 | 8 |
| 3 | 4 |
| 4 | 7 |
Таким образом, анализ функции позволяет получить полную картину ее изменений и определить основные характеристики. Это помогает лучше понять свойства функции и использовать их в различных математических задачах.
Поиск корней функции: основные подходы и методы
Существует несколько основных подходов и методов для поиска корней функции. Рассмотрим некоторые из них:
- Метод бисекции (деление отрезка): данный метод основан на принципе интервального деления. Суть метода заключается в разбиении отрезка на две части и нахождении корня в одной из этих частей. Процесс повторяется до достижения требуемой точности.
- Метод Ньютона: данный метод основан на принципе локальной линеаризации функции. Суть метода заключается в приближенном вычислении корня функции путем последовательных итераций. На каждой итерации используется линейное приближение функции.
- Метод простых итераций: данный метод основан на принципе построения итерационного процесса. Суть метода заключается в преобразовании уравнения с корнем в виде итерационного процесса с выражением корня функции в виде итерации.
- Метод секущих: данный метод основан на принципе построения секущей к графику функции. Суть метода заключается в построении секущей, проходящей через две точки графика функции, и последующем пересечении этой секущей с осью абсцисс.
Каждый из этих методов имеет свои преимущества и недостатки, и выбор конкретного метода зависит от задачи и свойств функции. Важно учитывать точность и скорость сходимости каждого метода, а также возможность возникновения ошибок и особенностей функции.
Определение точек экстремума функции: алгоритмы и рекомендации
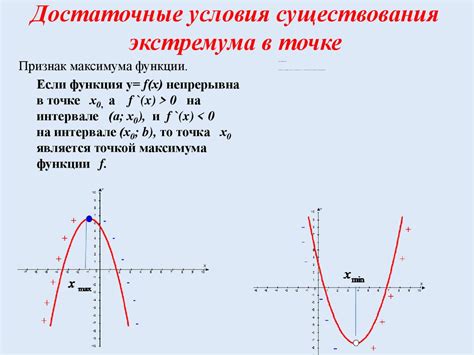
1. Исследование функции:
Перед тем, как найти точки экстремума функции, необходимо провести исследование самой функции. Это позволит определить, где она может иметь экстремумы. Исследование функции включает в себя нахождение области определения, точек разрыва и особых точек, а также анализ поведения функции на бесконечностях.
2. Нахождение производной функции:
Для нахождения точек экстремума необходимо вычислить производную функции и найти ее корни. Точки, в которых производная равна нулю или не существует, могут быть точками экстремума.
3. Анализ знаков производной:
Для определения типа экстремума в найденных точках, необходимо проанализировать знаки производной функции в этих точках. Если производная меняет знак с "плюса" на "минус" или с "минуса" на "плюс", то точка будет соответствовать экстремуму.
4. Проверка на вторую производную:
Чтобы убедиться, что найденные точки действительно являются экстремумами, необходимо проанализировать вторую производную функции в этих точках. Если вторая производная положительна, то точка будет являться точкой минимума, если отрицательна - точкой максимума. Если же вторая производная равна нулю или не существует, то точка будет требовать дополнительного исследования.
5. Проверка границ области определения:
Необходимо также проверить значения функции на границах области определения. Если значение функции в граничной точке больше (меньше) значений функции в точках экстремума, то граничная точка также может быть точкой экстремума.
6. Проверка особых точек:
Если были найдены особые точки (например, разрывы и вертикальные асимптоты), то необходимо анализировать поведение функции в этих точках отдельно. Они также могут быть точками экстремума.
Следуя этим алгоритмам и рекомендациям, вы сможете определить точки экстремума функции и более глубоко изучить ее поведение. Это поможет вам в решении задач, связанных с оптимизацией и нахождением значений функций.
Определение типа точек экстремума: практические советы
Для определения типа точек экстремума можно использовать следующие практические советы:
1. Анализ производной функции.
Один из основных способов определения типа точек экстремума - анализ производной функции. Если производная функции меняет знак с "плюса" на "минус" в точке экстремума, то это может указывать на максимум функции. Если производная функции меняет знак с "минуса" на "плюс" в точке экстремума, то это может указывать на минимум функции.
2. Анализ второй производной функции.
Вторая производная функции также может помочь в определении типа точек экстремума. Если вторая производная функции положительна в точке экстремума, то это может указывать на минимум функции. Если вторая производная функции отрицательна в точке экстремума, то это может указывать на максимум функции. Если вторая производная функции равна нулю в точке экстремума, то это может указывать на точку перегиба.
3. Анализ графика функции.
Анализ графика функции может дать дополнительную информацию о типе точек экстремума. Если график функции имеет локальный максимум в точке, то это может указывать на максимум функции. Если график функции имеет локальный минимум в точке, то это может указывать на минимум функции. Если график функции имеет точку, где график меняет свой наклон или кривизну, то это может указывать на точку перегиба.
При определении типа точек экстремума необходимо учитывать все указанные факторы и проводить анализ функции с использованием нескольких методов. Это позволит получить более точный результат и избежать возможных ошибок.
Вычисление значения функции в точках экстремума: несколько подходов
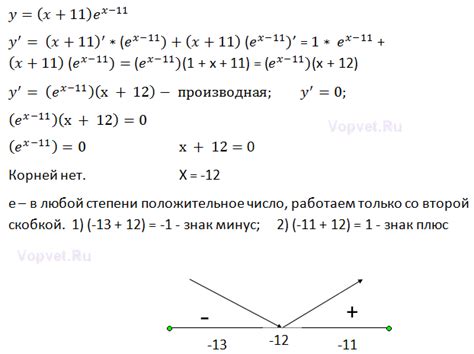
Для вычисления значения функции в точке экстремума можно использовать различные подходы:
1. Подставить значение аргумента в исходную функцию и выполнить соответствующие вычисления. Например, если найденная точка экстремума имеет координаты (x0, y0), то можно вычислить значение функции f(x) в этой точке подстановкой значения x = x0 и выполнением необходимых математических операций.
2. Воспользоваться графиком функции и найти значение функции в точке экстремума графически. На оси абсцисс откладывают значение аргумента, а на оси ординат - значение функции. Найденную точку экстремума можно отметить на графике и найти соответствующее значение функции, откладывая вертикальную линию от найденной точки до графика функции.
3. Воспользоваться аналитическими методами, если функция имеет аналитическое выражение. Например, если функция задана алгебраическим выражением, можно подставить значение аргумента в это выражение и выполнить необходимые вычисления для получения значения функции.
Выбор метода вычисления значения функции в точке экстремума зависит от доступных инструментов и особенностей самой функции. Используйте тот подход, который наиболее удобен в конкретной ситуации и предоставляет наиболее точные результаты.
Графическое представление точек экстремума: возможности исследования
Одним из способов исследования точек экстремума на графике является анализ изменения наклона касательной к кривой. В точках экстремума наклон графика меняется с положительного на отрицательный или наоборот. Это позволяет определить, что в данной точке находится максимум или минимум функции.
Другим способом исследования является анализ изменения выпуклости или вогнутости графика. В точках экстремума график может быть выпуклым или вогнутым в зависимости от типа экстремума. На графике это выражается в изменении формы кривой.
Также можно провести анализ значений функции в окрестности точек экстремума. Приближаясь к экстремуму справа или слева, значения функции будут увеличиваться или уменьшаться. Это помогает определить, является ли точка максимумом или минимумом.
Графическое представление точек экстремума позволяет получить наглядное представление о свойствах функции и легко определить наличие и положение экстремумов. Оно также помогает в выборе методов численного нахождения экстремумов, таких как метод дихотомии, метод золотого сечения и др.
При работе с графиками, важно учитывать, что точка экстремума может быть не единственной. Функция может иметь несколько максимумов и минимумов на заданном интервале. Поэтому при исследовании точек экстремума следует учитывать все возможные значения функции.
Выводы, сделанные на основе графического представления точек экстремума, могут быть полезными при решении различных задач и оптимизации функций. Этот метод анализа является доступным и понятным, что делает его важным инструментом для исследования экстремумов функций.
Проверка наличия точек экстремума с помощью производной: шаги и советы
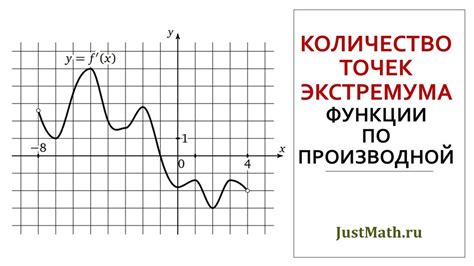
При анализе функций и определении их экстремальных точек мы можем использовать производные. Производная функции позволяет нам выявить моменты, когда функция имеет экстремумы. Ниже приведены шаги и советы по проверке наличия точек экстремума с помощью производной.
- Вычислите производную функции.
- Решите уравнение, полученное при приравнивании производной к нулю.
- Постройте таблицу знаков производной и определите интервалы, на которых производная положительна или отрицательна.
- Проверьте, является ли точка, в которой производная равна нулю или не существует, экстремальной.
- Проанализируйте значения функции в окрестности найденных точек экстремума, чтобы определить, является ли точка локальным максимумом или минимумом.
Кроме того, здесь есть несколько советов, которые помогут вам более точно определить сумму точек экстремума:
- Убедитесь, что вы правильно вычислили производную функции и решили уравнение, полученное при приравнивании производной к нулю.
- Не забывайте учитывать возможные граничные условия, которые могут оказывать влияние на наличие экстремумов.
- Проверьте полученные результаты путем построения графика функции. График даст вам визуальное представление о наличии и значении точек экстремума.
- Используйте дополнительные методы, такие как вторая производная для проверки характера точек экстремума.
Следуя этим шагам и советам, вы сможете успешно проверить наличие точек экстремума при анализе функций и определить их сумму.
Оценка значения функции в бесконечно удаленных точках: способы и примеры
Первый способ заключается в анализе поведения функции при стремлении аргумента к бесконечности. Если функция имеет предел при неограниченном стремлении аргумента, то значение функции в бесконечно удаленной точке будет равно этому пределу. Например, функция f(x) = \frac{1}{x} имеет предел 0 при x \to \infty, поэтому значение функции в бесконечно удаленной точке будет равно 0.
Второй способ заключается в рассмотрении асимптотического поведения функции. Если функция имеет асимптоту при неограниченном стремлении аргумента, то значение функции в бесконечно удаленной точке будет определяться этой асимптотой. Например, функция f(x) = \frac{x^2 + 2x + 3}{x} имеет горизонтальную асимптоту y = x + 2 при x \to \infty. Следовательно, значение функции в бесконечно удаленной точке будет равно \infty.
Третий способ заключается в использовании таблицы значений функции при больших значениях аргумента. Если функция обладает устойчивым поведением при больших значениях аргумента, то можно использовать некоторые интерполяционные методы для оценки значения функции в бесконечно удаленной точке. Например, рассмотрим функцию f(x) = \sqrt{x^2 - x}. Если построить таблицу значений функции при больших значениях x, можно заметить, что значения функции становятся все больше и больше. Следовательно, можно сделать вывод, что значение функции в бесконечно удаленной точке будет равно \infty.
| x | f(x) |
|---|---|
| 100 | 990.05 |
| 1000 | 998.02 |
| 10000 | 999.80 |
В данном разделе мы рассмотрели несколько способов оценки значения функции в бесконечно удаленных точках. Важно помнить, что использование этих способов требует внимательного анализа особенностей функции и может быть предметом дополнительного математического исследования.








