Треугольник - это одна из самых простых и фундаментальных геометрических фигур. Он состоит из трех сторон и трех углов, и его свойства и взаимоотношения могут быть использованы в широком спектре приложений, от инженерии до естественных наук.
Важной задачей в геометрии является нахождение длин сторон треугольника. Знание длин сторон позволяет вычислить другие характеристики треугольника, такие как периметр и площадь. Кроме того, оно необходимо для решения различных задач, связанных с треугольниками, например, для нахождения углов с помощью законов синусов и косинусов.
Одним из основных методов нахождения длин сторон треугольника является применение теоремы Пифагора. Она утверждает, что квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин его катетов. Эта теорема часто используется для нахождения длины стороны треугольника, если известны длины двух других сторон.
Знание длин сторон треугольника важно не только в математике, но и в реальном мире. Оно применяется в различных областях, таких как инженерия, архитектура и физика. Например, в инженерных расчетах необходимо знать длины сторон треугольника для определения механических свойств и прочности конструкций. А в архитектуре - для создания пропорциональных и эстетически приятных зданий.
Таким образом, нахождение длин сторон треугольника является важной задачей, имеющей как теоретическое, так и практическое значение. Знание длин сторон позволяет решать различные геометрические задачи, а также применять этот результат в широком спектре областей науки и техники.
Геометрические особенности поиска сторон треугольника
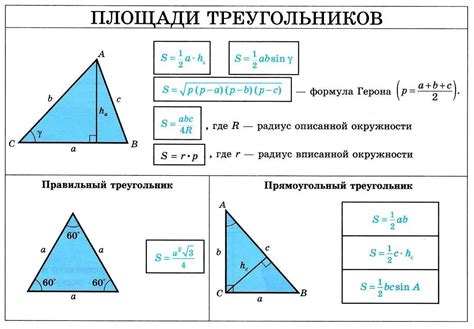
Для нахождения длин сторон треугольника можно использовать различные методы и формулы. Одним из самых простых способов является использование теоремы Пифагора, которая применяется для прямоугольных треугольников. Другими словами, если известны длины катетов треугольника, можно найти длину гипотенузы.
Если треугольник не является прямоугольным, можно применить теорему косинусов или теорему синусов. Теорема косинусов позволяет найти длину одной из сторон треугольника, используя длины других двух сторон и косинус угла между ними. Теорема синусов же позволяет найти длину одной из сторон треугольника, используя длины других двух сторон и синус угла, противолежащего этой стороне.
Еще одним методом нахождения сторон треугольника является использование тригонометрических функций (синуса, косинуса и тангенса) и известных углов треугольника. Применение этих функций позволяет находить длины сторон треугольника по известным углам и другим известным сторонам.
Геометрические особенности поиска сторон треугольника зависят от его формы и углов. Нахождение сторон треугольника является важным шагом в решении задач с участием треугольников, таких как вычисление площади, определение высот и построение синусовидных тригонометрических функций.
Таблица ниже представляет особенности поиска сторон треугольника в зависимости от его формы:
| Треугольник | Особенность |
|---|---|
| Равносторонний треугольник | Все стороны равны |
| Равнобедренный треугольник | Две стороны равны |
| Прямоугольный треугольник | Применение теоремы Пифагора |
| Треугольник произвольной формы | Применение теоремы косинусов или теоремы синусов |
Основные понятия и определения
Для полного понимания значения поиска сторон треугольника необходимо ознакомиться с несколькими основными понятиями и определениями:
- Треугольник - это геометрическая фигура, которая состоит из трех отрезков, называемых сторонами, и трех углов, образованных этими сторонами.
- Стороны треугольника - отрезки, соединяющие вершины треугольника. Каждая сторона имеет длину, которая может быть измерена в единицах длины, таких как сантиметры или метры.
- Вершины треугольника - точки пересечения сторон треугольника. Обозначаются обычно заглавными буквами латинского алфавита, например, A, B и C.
- Углы треугольника - образованы пересечением сторон треугольника и обозначаются маленькими буквами греческого алфавита, например, α, β и γ.
- Геометрические особенности треугольника - треугольники могут быть различных типов в зависимости от свойств и условий их сторон и углов, например, прямоугольные, равнобедренные или равносторонние.
Основные понятия и определения, связанные со сторонами треугольника, являются основой для дальнейшего изучения геометрии треугольников и активного применения при решении различных задач и проблем в разных областях науки и техники.
Взаимосвязь между сторонами треугольника

В геометрии треугольника взаимосвязь между его сторонами играет важную роль при решении различных задач. Понимание этой взаимосвязи помогает нам определить углы и длины сторон треугольника, а также использовать их для нахождения различных параметров.
Например, существует ряд теорем, которые позволяют нам определить длину одной стороны треугольника, если известны длины других сторон и углы. Одна из таких теорем - теорема косинусов, которая устанавливает взаимосвязь между длинами сторон и углами треугольника.
Теорема косинусов гласит:
- Величина квадрата длины одной стороны треугольника равна сумме квадратов длин двух других сторон, умноженной на два раза произведение этих сторон на косинус соответствующего им угла.
- Формула теоремы косинусов может быть выражена следующим образом: a^2 = b^2 + c^2 - 2bc*cosA, где a, b и c - длины сторон треугольника, A - угол, соответствующий стороне a.
Эта формула позволяет находить длину одной из сторон треугольника, если известны длины остальных сторон и угол между ними.
Также существуют теоремы, которые позволяют нам определить отношения между сторонами треугольника. Например, в прямоугольном треугольнике с длинами катетов a и b и гипотенузой c справедливо соотношение: a^2 + b^2 = c^2. Это соотношение называется теоремой Пифагора и широко применяется при решении задач по нахождению длин сторон треугольника.
Таким образом, взаимосвязь между сторонами треугольника является важным инструментом для решения задач и определения различных параметров треугольника. Знание соответствующих теорем позволяет нам анализировать и использовать стороны треугольника для нахождения углов, длин сторон и других характеристик треугольника.
Теорема Пифагора и ее применение
Формула теоремы Пифагора выглядит следующим образом: a² + b² = c², где a и b - длины катетов, а c - длина гипотенузы.
Теорема Пифагора имеет множество практических применений в различных областях науки и техники. Первоначально она была использована для решения задач связанных с построением прямоугольников и диагоналей в них. Сегодня она находит применение в архитектуре, при решении геодезических задач, в физике и многих других областях.
Например, теорема Пифагора используется при рассчете расстояний на плоской поверхности. Если известны координаты двух точек на плоскости, то по формуле теоремы Пифагора можно найти расстояние между ними.
Также теорема Пифагора используется при решении задач связанных с электрическими цепями. Например, для нахождения значения резистора в электрической цепи, зная значения сопротивлений в других участках цепи.
Теоремы о треугольниках с равными сторонами
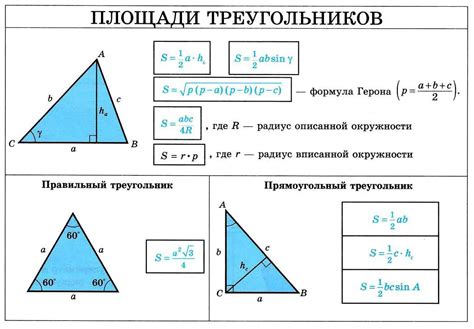
Теорема 1: В равностороннем треугольнике все углы равны 60 градусам.
Доказательство: Разделим равносторонний треугольник на два равносторонних треугольника, соединив середины сторон треугольника прямыми линиями. Таким образом, получаем шесть равных треугольников. У каждого треугольника угол равен 180 градусам (сумма углов треугольника), а так как углы равных треугольников равны, то в каждом из этих треугольников угол равен 30 градусам. Значит, все углы исходного равностороннего треугольника равны 30 градусам.
Теорема 2: В равностороннем треугольнике высота является биссектрисой и медианой одновременно.
Доказательство: Рассмотрим медиану и высоту, проведенные из одной вершины равностороннего треугольника. Так как треугольник равносторонний, то высота, как и медиана, делит основание треугольника пополам. Кроме того, по теореме о том, что в треугольнике, делящем основание пропорционально, стороны треугольника делятся пополам, высота является биссектрисой угла при вершине треугольника. Таким образом, высота является и медианой, и биссектрисой в равностороннем треугольнике.
Теорема 3: Вписанный в равносторонний треугольник круг содержит центральный угол в 120 градусов.
Доказательство: Рассмотрим центральный угол треугольника, составленный прямыми линиями, соединяющими вершины треугольника с центром описанной окружности. Так как в равностороннем треугольнике все углы равны 60 градусам, то сумма углов составляющих центральный угол равна 180 градусам. Значит, центральный угол вписанного в равносторонний треугольник круга равен 120 градусам.
Применение поиска сторон треугольника
1. Решение геометрических задач.
Поиск сторон треугольника позволяет находить решения для различных геометрических задач. Например, зная длины сторон треугольника, можно вычислить его площадь, периметр, а также различные углы и высоты.
2. Работа с картографическими данными.
В картографии часто требуется находить расстояние между точками на карте. В некоторых случаях можно приближенно считать, что расстояние между точками - это длина отрезка прямой линии, но в реальности поверхность Земли имеет сферическую форму и для точного расчета расстояний необходимо использовать геодезические методы. Поиск сторон треугольника может быть одним из таких методов.
3. Архитектурное проектирование и строительство.
В архитектуре и строительстве треугольники широко используются для расчета размеров, углов и пропорций зданий. Поиск сторон треугольника играет важную роль в этих расчетах, позволяя получить точные и надежные данные.
4. Тригонометрические вычисления.
Тригонометрия - это раздел математики, изучающий отношения между углами и сторонами в треугольниках. Поиск сторон треугольника является важной частью тригонометрии, так как позволяет вычислять значения тригонометрических функций (синус, косинус, тангенс и т.д.) и использовать их в решении различных задач.
5. Компьютерная графика и моделирование.
В компьютерной графике и моделировании треугольники используются для построения различных геометрических объектов, таких как полигоны, многоугольники и другие. Поиск сторон треугольника позволяет определить положение и размеры этих объектов на экране.
Таким образом, поиск сторон треугольника имеет широкое применение в различных областях и является основой для выполнения различных геометрических вычислений.
Измерение длин сторон в планировании земельных участков
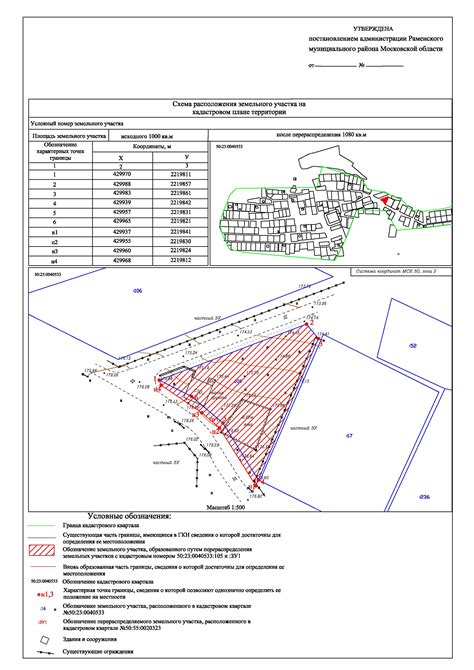
Измерение длин сторон треугольника имеет важное значение в планировании земельных участков. Земельные участки обычно имеют треугольную форму или приближенную к ней, поэтому знание длин сторон треугольника позволяет определить площадь участка и его геометрические особенности.
Измерение длин сторон треугольника производится с помощью линейки, теодолита или геодезической станции. Полученные данные заносятся в карту участка, что позволяет точно определить его границы и форму. Это особенно важно при планировании застройки или при проведении границевых работ.
Знание длин сторон треугольника также позволяет вычислить его высоту и углы. Это полезно при проектировании строений на участке, таких как дома, дачи или промышленные здания. Высота треугольника и углы его прилегающих сторон могут быть использованы для определения оптимального расположения строений, а также для расчета прочности конструкций.
Таким образом, измерение длин сторон треугольника является важной частью планирования земельных участков. Это позволяет определить границы участка, его форму и геометрические особенности, а также использовать полученные данные при проектировании строений.
Вычисление площади треугольника и других фигур
Вычисление площади треугольника
Площадь треугольника является одной из основных характеристик этой геометрической фигуры. Площадь можно вычислить, зная длины двух сторон и угол между ними, или зная длины всех трех сторон. Для этого существует несколько формул, основанных на принципе геометрических вычислений.
Одна из самых простых формул для вычисления площади треугольника называется "Полупроизведение сторон и синус угла". Она выглядит следующим образом:
S = (a * b * sin(C)) / 2
Где S - площадь треугольника, a и b - длины сторон, C - угол между этими сторонами. Здесь используется тригонометрическая функция синус.
Также можно использовать формулу Герона для вычисления площади треугольника, которая основана на полупериметре и длинах трех сторон. Формула выглядит следующим образом:
S = sqrt(s * (s - a) * (s - b) * (s - c))
Где S - площадь треугольника, s - полупериметр (сумма длин всех сторон, деленная на 2), a, b и c - длины сторон.
Вычисление площади других фигур
Помимо треугольника, площадь можно вычислить и для других геометрических фигур. Некоторые из них:
Квадрат: площадь квадрата вычисляется по формуле S = a * a, где S - площадь, a - длина стороны.
Прямоугольник: площадь прямоугольника вычисляется по формуле S = a * b, где S - площадь, a и b - длины сторон прямоугольника.
Круг: площадь круга вычисляется по формуле S = pi * r * r, где S - площадь, pi - число пи (приблизительно 3,14), r - радиус.
Это лишь некоторые примеры вычисления площади различных геометрических фигур. В общем случае, для каждой фигуры существуют свои формулы, основанные на ее геометрических параметрах.








