Производная функции – это одно из самых важных понятий математического анализа.
Она позволяет найти скорость изменения функции в каждой точке её области определения.
Производная по определению – это один из способов вычисления производной.
Для определения производной по определению мы используем предел и формулу:
f'(x) = lim[(f(x + h) - f(x))/h] при h -> 0
Данная формула показывает, как изменяется функция f(x) при изменении аргумента x на некоторую малую величину h.
Если функция гладкая (имеет непрерывные производные), то в каждой точке x у неё есть производная.
Таким образом, производная функции позволяет найти наклон касательной к графику функции в каждой его точке.
Для вычисления производной по определению нужно выполнить несколько шагов.
Во-первых, выразить функцию f(x) в виде аналитического выражения.
Затем, применяя формулу производной по определению, вычислить предел при h, стремящимся к 0.
Приведем простой пример вычисления производной. Пусть у нас есть функция f(x) = x^2.
Подставим ее в формулу производной по определению:
f'(x) = lim[(f(x + h) - f(x))/h] при h -> 0
f'(x) = lim[( (x + h)^2 - x^2 )/h] при h -> 0
f'(x) = lim[( x^2 + 2hx + h^2 - x^2)/h] при h -> 0
f'(x) = lim[( 2hx + h^2)/h] при h -> 0
f'(x) = lim[2x + h] при h -> 0
f'(x) = 2x
Таким образом, производная функции f(x) = x^2 равна f'(x) = 2x.
Что такое производная по определению?

Производная функции в точке определяется по определению как предел отношения приращения функции к приращению аргумента при бесконечно малом приращении аргумента. Формально, производная функции f(x) в точке x_0 вычисляется по следующей формуле:
В данной формуле, f(x) - функция, x_0 - точка, в которой вычисляется производная, h - бесконечно малое приращение аргумента.
Вычисление производной по определению позволяет получить точное значение производной функции в заданной точке. Однако, процесс вычисления может быть достаточно сложным в случае функций с большим числом переменных или сложной структурой.
Пример вычисления производной по определению:
- Рассмотрим функцию f(x) = x^2. Чтобы вычислить производную по определению, нужно выразить приращение функции и приращение аргумента через х и h:
- Приращение функции: f(x + h) - f(x) = (x + h)^2 - x^2 = x^2 + 2xh + h^2 - x^2 = 2xh + h^2.
- Приращение аргумента: h.
- f'(x) = lim(h->0) (2xh + h^2)/h = lim(h->0) 2x + h = 2x.
Это лишь один из возможных примеров вычисления производной по определению для простой функции. В общем случае, процесс может быть более сложным, но все же основные принципы остаются теми же.
Определение и примеры вычисления
Для вычисления производной по определению, необходимо использовать предел, где h стремится к нулю:
f'(x) = lim(h → 0) (f(x+h) - f(x))/h
Например, рассмотрим функцию f(x) = x^2. Для вычисления производной в точке x=a, нужно заменить в формуле функцию f(x) на f(a) и вычислить предел:
f'(a) = lim(h → 0) (f(a+h) - f(a))/h
Подставляем функцию f(x) = x^2:
f'(a) = lim(h → 0) ((a+h)^2 - a^2)/h
Раскрываем скобки и упрощаем выражение:
f'(a) = lim(h → 0) (a^2 + 2ah + h^2 - a^2)/h = lim(h → 0) (2ah + h^2)/h = lim(h → 0) (2a + h)
В пределе при h→0, выражение превращается в 2a, поэтому производная функции f(x) = x^2 равна 2a.
Таким образом, производная функции f(x) = x^2 равна 2x.
Определение производной функции

Определение производной функции формально записывается следующим образом:
Пусть f(x) - функция, определенная на открытом интервале, содержащем точку x0. Производная функции в точке x0 обозначается как f'(x0) или dy/dx и определяется по формуле:
f'(x0) = limx→x0 (f(x) - f(x0))/(x - x0) |
Интуитивно, производная функции в точке x0 показывает, насколько быстро значение функции меняется, когда x приближается к x0. Если производная положительна, функция возрастает в данной точке, если отрицательна - убывает, а если равна нулю - имеется экстремум (минимум или максимум).
Например, рассмотрим функцию f(x) = x2. Ее производная может быть найдена следующим образом:
f'(x) = limh→0 (f(x+h) - f(x))/(h) f'(x) = limh→0 ((x+h)2 - x2)/(h) f'(x) = limh→0 (x2 + 2xh + h2 - x2)/(h) f'(x) = limh→0 (2xh + h2)/(h) f'(x) = limh→0 2x + h f'(x) = 2x |
Таким образом, производная функции f(x) = x2 равна 2x. Это означает, что скорость изменения значений функции f(x) равна удвоенному значению аргумента x.
Дифференциальный коэффициент и пределы
Дифференциальный коэффициент функции f(x) в точке x = a определяется как значение предела отношения приращения функции к приращению аргумента:
f'(a) = limh→0 (f(a + h) - f(a)) / h
где lim обозначает предел, а h - маленькое число, стремящееся к нулю.
Дифференциальный коэффициент показывает, как изменяется значение функции при изменении аргумента вблизи данной точки. Он является касательной к графику функции в этой точке.
Например, если функция f(x) = x^2, то дифференциальный коэффициент в точке x = 2 будет:
f'(2) = limh→0 ((2 + h)^2 - 2^2) / h
Раскрывая скобки и сокращая, получим:
f'(2) = limh→0 (4 + 4h + h^2 - 4) / h = limh→0 (4h + h^2) / h = limh→0 4 + h = 4
Таким образом, дифференциальный коэффициент функции f(x) = x^2 в точке x = 2 равен 4. Это означает, что скорость изменения функции в этой точке равна 4.
Производная как скорость изменения
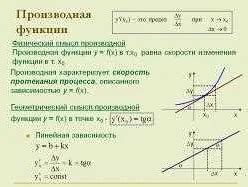
Для понимания этой концепции рассмотрим пример. Пусть у нас есть функция, заданная уравнением y = 3x^2, где x - аргумент, а y - значение функции.
Мы можем рассчитать производную этой функции в любой точке, используя определение. Например, для точки x = 2 мы можем рассчитать производную следующим образом:
Производная в точке x = 2:
lim(h→0) [f(2 + h) - f(2)] / h
lim(h→0) [(3(2 + h)^2) - (3(2)^2)] / h
lim(h→0) [(3(4 + 4h + h^2)) - (12)] / h
lim(h→0) [(12 + 12h + 3h^2) - 12] / h
lim(h→0) (12h + 3h^2) / h
lim(h→0) 12 + 3h
= 12
Таким образом, мы получили, что производная функции y = 3x^2 в точке x = 2 равна 12. Это означает, что функция меняется со скоростью 12 единиц на каждую единицу изменения аргумента в этой точке.
Таким образом, производная является важным инструментом в математике и физике, позволяющим изучать скорость изменения функций и расчитывать траектории движения, скорости и ускорения объектов.
Геометрическая интерпретация производной
Производная функции в точке является скоростью изменения значения функции в данной точке. Графически производная функции в точке равна тангенсу угла наклона касательной к графику функции в этой точке.
Например, рассмотрим функцию f(x) = x^2. Ее график представляет собой параболу, которая открывается вверх.
Если мы возьмем точку на графике, например, x = 2, то тангенс угла наклона касательной в этой точке будет равен производной функции в этой точке. В данном случае, производная функции f(x) = x^2 равна f'(x) = 2x. Таким образом, в точке x = 2 производная равна 4, что означает, что скорость изменения значения функции в этой точке составляет 4.
Таким образом, геометрическая интерпретация производной позволяет нам понять, как функция меняется в каждой точке и описать ее поведение на всем протяжении графика.
Производная и тангенс угла наклона
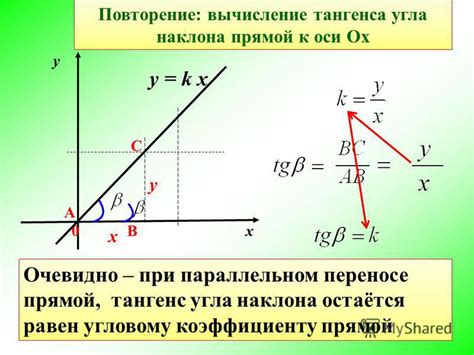
Для того чтобы вычислить тангенс угла наклона (производную) функции y=f(x) в данной точке, необходимо следовать следующим шагам:
- Найти значение производной функции f(x), то есть f'(x).
- Заменить x на значение данной точки в производной функции и вычислить полученное значение. Обозначим это значение как m.
- m является тангенсом угла наклона, так как тангенс угла наклона определяется как отношение прилежащего катета к противолежащему катету в прямоугольном треугольнике, где прилежащий катет равен deltax (изменение x) и противолежащий катет равен deltay (изменение y).
Для наглядности вычисления тангенса угла наклона можно использовать таблицу значений функции. Рассмотрим пример:
| x | f(x) | f'(x) | m |
|---|---|---|---|
| 1 | 3 | 2 | 2 |
| 2 | 5 | 2 | 2 |
| 3 | 7 | 2 | 2 |
В данном примере, когда значение x равно 1, 2 и 3, производная функции равна 2, а значение тангенса угла наклона равно 2. Это говорит о том, что функция имеет одинаковый наклон при изменении x в данных точках.








