Когда мы говорим о нахождении нуля функции, мы обычно имеем в виду определение значения аргумента, при котором функция обращается в ноль. Это важное понятие в математике и физике, и его понимание позволяет решать различные задачи и уравнения.
Найти ноль функции означает найти решение уравнения f(x) = 0. Другими словами, мы ищем значение аргумента x, при котором функция f(x) равна нулю. Это позволяет нам найти точку на графике функции, где она пересекает ось абсцисс, итак определить свойства функции и решить различные задачи.
Для примера рассмотрим функцию f(x) = x^2 - 4. Найдем ноль этой функции. Для этого мы должны решить уравнение x^2 - 4 = 0. Применяя различные методы, мы можем найти, что решением этого уравнения являются значения x = 2 и x = -2. Именно в этих точках функция f(x) обращается в ноль.
Найти ноль функции - это важный шаг при решении уравнений и задач в математике и физике. Это позволяет определить положение и свойства графика функции и дает нам возможность решать различные задачи. Понимание этого понятия является ключевым для успешного изучения и применения математики и физики.
Что это значит и почему это важно?

Значение нуля функции
Нахождение нуля функции очень важно в различных областях математики и науки, так как это позволяет решать уравнения, моделировать явления и анализировать поведение функций.
Существует несколько методов для нахождения нулей функций, включая графический метод, метод подстановки, метод итераций (метод простой итерации) и методы численного анализа, такие как метод бисекции, метод Ньютона и метод секущих.
Для наглядности приведем примеры функций и их нулей:
- Функция f(x) = x^2 - 4 имеет нули при x = -2 и x = 2.
- Функция f(x) = sin(x) имеет нули при x = 0, x = π, x = 2π и так далее.
- Функция f(x) = e^x - 1 имеет нуль при x = 0.
Основное значение поиска нуля функции заключается в том, что оно помогает нам понять, где и как функция пересекает ось абсцисс и дает нам возможность решать уравнения вида f(x) = 0. Это важный инструмент на практике и в научных исследованиях.
Почему поиск нуля функции является важным этапом?

Поиск нуля функции имеет широкое применение в различных областях. В физике, например, нахождение нуля функции может помочь в определении равновесного состояния системы или в решении задач о движении объектов. В экономике ноль функции может использоваться для нахождения точки безубыточности или определения максимальной прибыли.
Поиск нуля функции также позволяет решать уравнения, приводить функции к каноническому виду и строить графики. Он помогает понять свойства функций, такие как монотонность, возрастание или убывание, экстремумы и точки перегиба.
Особое внимание уделяется корням функций, когда необходимо найти все значения аргумента, при которых функция равна 0. Поиск корней функции может быть выполнен с помощью аналитических методов (например, методом подстановки) или численных (например, методом половинного деления или методом Ньютона).
В итоге, поиск нуля функции является важным этапом, так как позволяет получить информацию о свойствах функции, решить уравнения и применить полученные знания в практических задачах.
Основные методы поиска нуля функции
Найти ноль функции означает найти значение аргумента (или значения аргументов), при котором значение функции равно нулю. Это может быть полезно, например, для определения точек пересечения графика функции с осью абсцисс или для решения уравнений.
Существует несколько основных методов для поиска нуля функции:
1. Метод подстановки. Данный метод заключается в замене значения функции переменной и последующем решении уравнения. Например, если нам дана функция f(x) = x^2 - 4 и мы хотим найти ее нули, мы можем подставить значение нуля вместо x и решить уравнение: f(0) = 0^2 - 4 = -4. Таким образом, ноль функции f(x) = x^2 - 4 не существует.
2. Графический метод. Для некоторых функций можно построить график и визуально определить точку (или точки) пересечения с осью абсцисс. Например, для функции f(x) = x^2 - 4 график будет иметь форму параболы, и пересечение с осью абсцисс будет происходить в точках (-2, 0) и (2, 0). То есть нули функции f(x) = x^2 - 4 равны -2 и 2.
3. Метод численных итераций. Данный метод основывается на последовательном приближении к решению уравнения с помощью итераций. Например, для функции f(x) = x^2 - 4 можно выбрать начальное приближение (например, x0 = 1) и затем последовательно вычислять значения xi+1 = xi - f(xi)/f'(xi), где f'(xi) - производная функции f(x) в точке xi. При достаточном количестве итераций этот метод может сойтись к нулю функции.
4. Аналитический метод. В некоторых случаях нули функции можно найти аналитически с помощью математических методов, таких как факторизация, исключение переменных или применение формулы корней уравнения. Например, для функции f(x) = x^2 - 4 нули можно найти аналитически с помощью факторизации: f(x) = (x - 2)(x + 2), откуда x = 2 и x = -2.
Знание и применение этих методов помогают в решении различных математических задач, связанных с поиском нуля функции.
Метод дихотомии
Основная идея метода дихотомии состоит в следующем:
- На первом шаге определяется интервал, в котором находится корень функции. Интервал должен быть таким, чтобы на его концах функция принимала значения с разными знаками.
- Затем интервал делится пополам, определяя середину отрезка.
- Значение функции в середине отрезка сравнивается с нулем.
- Если значение функции в середине отрезка равно нулю или достаточно близко к нулю, то середина отрезка является корнем функции.
- Если значение функции в середине отрезка имеет другой знак, чем значения на концах отрезка, то корень функции находится в одной из половин интервала.
- Выбирается та половина, в которой значение функции имеет такой же знак, как и на конце отрезка, и процесс повторяется с новым интервалом.
- Повторение процесса продолжается до тех пор, пока не будет достигнута существенная близость к нулю значения функции в середине отрезка, либо когда достигнута необходимая точность решения.
Применение метода дихотомии позволяет с высокой точностью находить корни функций и решать уравнения. Однако необходимо учитывать, что для применения метода требуется знать интервал, в котором находится корень функции, и функция должна быть непрерывной на этом интервале.
Пример использования метода дихотомии:
import math
def f(x):
return x**2 - 4
a = 0
b = 3
epsilon = 0.001
while abs(b-a) > epsilon:
c = (a + b) / 2
if f(c) == 0:
break
if f(a) * f(c) В данном примере метод дихотомии используется для нахождения корня уравнения x^2 - 4 = 0 на интервале [0, 3].
Метод хорд
Алгоритм метода хорд очень прост:
- Задаем начальные значения точек а и б на исследуемом интервале [a, b] таким образом, чтобы значения функции в этих точках имели разные знаки: f(a) * f(b)
- Находим точку пересечения хорды, соединяющей точки (a, f(a)) и (b, f(b)), с осью OX. Эта точка и будет приближенным значением корня функции.
- Для следующей итерации выбираем в качестве новых точек а и б такие точки, чтобы они опять имели разные знаки функции.
- Повторяем шаги 2 и 3 до достижения заданной точности.
Чтобы увидеть, как работает метод хорд, рассмотрим пример. Решим уравнение sin(x) - x = 0 на отрезке [0, 1].
Таблица ниже показывает значения функции в начальных точках a и b на каждой итерации метода хорд, а также приближенное значение корня функции, найденное после каждой итерации.
| Итерация | a | b | f(a) | f(b) | Приближенное значение корня |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0.84147 | 0.54030 |
| 2 | 0.54030 | 1 | -0.42552 | 0.84147 | 0.75042 |
| 3 | 0.75042 | 1 | -0.13715 | 0.84147 | 0.83477 |
| 4 | 0.83477 | 1 | -0.04452 | 0.84147 | 0.86190 |
| 5 | 0.86190 | 1 | -0.01438 | 0.84147 | 0.87245 |
| 6 | 0.87245 | 1 | -0.00461 | 0.84147 | 0.87778 |
Метод хорд сходится быстро к точному значению корня функции, однако его сходимость может быть медленной в некоторых случаях или при плохом выборе начальных точек a и b. В таких случаях более эффективными методами являются методы Ньютона или секущих.
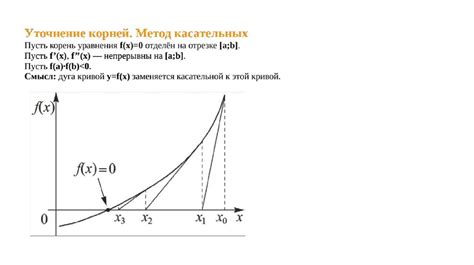
Метод Ньютона

Идея метода Ньютона заключается в следующем. Пусть у нас есть функция f(x), и мы хотим найти ее корень x0. Метод Ньютона начинается с какого-то начального приближения x1 и продолжает итерироваться с использованием формулы:
xn+1 = xn - f(xn) / f'(xn)
где f'(xn) означает производную функции f(x) в точке xn. Итерационный процесс продолжается до достижения необходимой точности, когда |f(xn)| становится меньше заданного значения.
Применение метода Ньютона позволяет находить корни функций в достаточно короткое время, особенно когда производная функции легко вычисляема. Кроме того, данный метод имеет квадратичную сходимость, что означает удвоение числа верных цифр на каждой итерации.
Пример использования метода Ньютона:
| Функция | Начальное приближение | Корень |
|---|---|---|
| sin(x) | 1 | 3.141592653589793 |
| x3 - 2x2 - 11x + 12 | 2 | 2.035276180410083 |
В первом примере, мы ищем корень функции sin(x) с начальным приближением x = 1, и метод Ньютона находит решение x = 3.141592653589793. Во втором примере, мы находим корень функции x3 - 2x2 - 11x + 12 с начальным приближением x = 2, и метод Ньютона дает решение x = 2.035276180410083.
Примеры нахождения нуля функции
Чтобы понять, как находить нуль функции, давайте рассмотрим несколько примеров.
Пример 1:
Дана функция f(x) = x^2 - 4.
Чтобы найти нуль функции, нужно решить уравнение f(x) = 0. В данном случае получаем x^2 - 4 = 0.
Преобразуем уравнение: x^2 = 4.
Извлекаем квадратный корень: x = ±2.
Таким образом, нулями функции f(x) = x^2 - 4 являются числа -2 и 2.
Пример 2:
Дана функция g(x) = 3x + 2.
Для нахождения нуля функции решаем уравнение g(x) = 0. В данном случае получаем 3x + 2 = 0.
Преобразуем уравнение: 3x = -2.
Делим обе части на 3: x = -2/3.
Таким образом, нулем функции g(x) = 3x + 2 является число -2/3.
Пример 3:
Дана функция h(x) = e^x - 1.
Для нахождения нуля функции решаем уравнение h(x) = 0. В данном случае получаем e^x - 1 = 0.
Преобразуем уравнение: e^x = 1.
Применяем обратную функцию натурального логарифма: x = ln(1).
Заметим, что ln(1) = 0, поэтому нулем функции h(x) = e^x - 1 является число 0.
Таким образом, нули функции могут быть как целыми числами, так и дробями или иррациональными числами, в зависимости от формы функции и ее уравнения. Нахождение нуля функции позволяет найти точки пересечения ее графика с осью абсцисс и определить, при каких значениях аргумента функция равна нулю.








