Множество решений системы неравенств является основной концепцией в математике, используемой для описания ситуаций, в которых имеется некоторый набор условий, и требуется найти все значения переменных, которые удовлетворяют этим условиям. В общем случае, множество решений системы неравенств является подмножеством числового множества и может быть описано в виде отрезков, интервалов, или комбинации этих элементов.
Для понимания концепции множества решений системы неравенств рассмотрим простой пример. Предположим, у нас есть система двух неравенств: 3x + 2y ≤ 10 и x + y ≥ 5. Здесь переменные x и y могут принимать различные значения, при условии, что эти значения удовлетворяют обоим неравенствам одновременно. Для определения множества решений мы будем искать пересечение всех значений, удовлетворяющих первому неравенству, и значений, удовлетворяющих второму неравенству. Это пересечение будет являться искомым множеством решений.
Таким образом, множество решений системы неравенств – это множество значений переменных, удовлетворяющих всем неравенствам данной системы. Оно может быть представлено в виде графического изображения на плоскости или числовыми интервалами.
Разъяснение множества решений системы неравенств
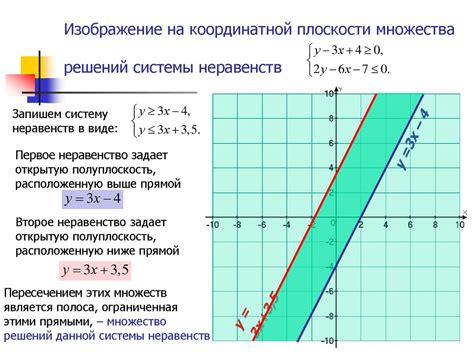
Множество решений системы неравенств представляет собой набор всех значений переменных, которые удовлетворяют всем неравенствам системы. В отличие от решений системы уравнений, множество решений системы неравенств может быть более сложным и содержать не только конкретные значения, но и неравенства между переменными.
Предположим, у нас есть следующая система неравенств:
| Неравенство | Решение |
|---|---|
| x - 2 < 5 | x < 7 |
| 3y + 4 > 10 | y > 2 |
В данном примере первое неравенство указывает на то, что переменная x должна быть меньше 7, а второе неравенство говорит о том, что переменная y должна быть больше 2. Система неравенств имеет множество решений, которое представляет собой пересечение двух множеств: множества значений x (где x < 7) и множества значений y (где y > 2).
Если мы нарисуем координатную плоскость и отметим на ней множества значений переменных x и y, то множество решений будет представлять собой область, где оба множества пересекаются. В данном случае, множество решений будет представлять собой все значения x меньше 7 и все значения y больше 2.
Множество решений системы неравенств может представляться разными способами, включая формальное описание, неравенства или графическое представление на координатной плоскости. Важно понимать, что множество решений представляет собой все значения переменных, которые удовлетворяют всем неравенствам системы.
Определение множества решений
Множество решений системы неравенств представляет собой совокупность всех значений, при которых выполняются все неравенства системы.
Для определения множества решений необходимо рассмотреть каждое неравенство по отдельности и найти значения переменных, при которых это неравенство выполнено. После этого необходимо учесть все значения, которые удовлетворяют всем неравенствам одновременно.
Множество решений может быть пустым, если значения переменных не удовлетворяют ни одному неравенству системы. Однако в большинстве случаев множество решений может быть неограниченным или ограниченным.
Чтобы проиллюстрировать это, рассмотрим пример:
| Система неравенств | Множество решений |
|---|---|
| {x ≥ 2, y | {(2, 3), (3, 2), (4, 1), (5, 0), ...} |
В данном примере множество решений состоит из всех пар чисел (x, y), которые удовлетворяют обоим неравенствам. Значения переменных x и y могут быть любыми числами, главное, чтобы они удовлетворяли неравенствам системы.
Как найти множество решений системы неравенств

Множество решений системы неравенств представляет собой набор значений переменных, при которых все неравенства выполнены одновременно. Чтобы найти это множество, следует применить следующие шаги:
- Решить каждое неравенство отдельно. Для этого нужно выражение неравенства привести к виду, где переменная находится в одной части, а константы – в другой.
- Построить графическое представление каждого решения. Неравенства обычно представляются на числовой оси либо на координатной плоскости.
- Определить множество значений переменных, при которых все неравенства выполняются.
Пример: рассмотрим систему неравенств:
- 2x + 3
- 4x - 7 > 1
Шаг 1: выразим переменную в терминах неравенства:
- x
- x > 2
Шаг 2: построим графическое представление каждого решения. На числовой оси отметим точки 1 и 2 с помощью открытых или закрытых круглых скобок.
Шаг 3: определим множество значений переменной, которые удовлетворяют обоим неравенствам. В данном случае, такого значения не существует, так как интервалы из шага 2 не пересекаются.
Таким образом, множество решений данной системы неравенств является пустым множеством.
Примеры множества решений
Для наглядного объяснения понятия "множество решений системы неравенств" рассмотрим несколько примеров:
Пример 1:
Рассмотрим систему неравенств:
2x + 3y ≤ 12
4x - y > 5
Для начала найдем границы области, ограниченной данными неравенствами. Решим оба неравенства как равенства:
2x + 3y = 12
4x - y = 5
После решения этих уравнений получим точки пересечения границ:
Точка А: (3, 2)
Точка В: (2, -3)
Точка С: (7, -9)
Теперь рассмотрим подобласти, полученные отделением каждого неравенства:
1) Для 2x + 3y ≤ 12:
Возьмем произвольную точку вне области, например (4, 2). Подставим ее в неравенство:
2 * 4 + 3 * 2 = 14 > 12
Таким образом, точка (4, 2) не принадлежит области решений данного неравенства.
Область решений неравенства 2x + 3y ≤ 12 представляет собой полуплоскость ниже линии, проходящей через точки А и Б.
2) Для 4x - y > 5:
Возьмем произвольную точку вне области, например (3, 0). Подставим ее в неравенство:
4 * 3 - 0 = 12 > 5
Таким образом, точка (3, 0) принадлежит области решений данного неравенства.
Область решений неравенства 4x - y > 5 представляет собой полуплоскость выше линии, проходящей через точку С и далее вправо.
Теперь найдем общую область, удовлетворяющую обоим неравенствам:
Область решений системы неравенств представляет собой пересечение областей, полученных для каждого неравенства отдельно.
Итоговая область решений представляет собой треугольник, ограниченный линиями, проходящими через точки А, Б и С.
Пример 2:
Рассмотрим систему неравенств:
3x - 2y ≤ 6
5x + y > 1
Повторим уже известный нам алгоритм:
1) Найдем точки пересечения границ:
Точка А: (3, 0)
Точка В: (-1, 2)
Точка С: (-1, 6)
2) Рассмотрим подобласти, полученные отделением каждого неравенства:
Область решений неравенства 3x - 2y ≤ 6 представляет собой полуплоскость ниже линии, проходящей через точки А и В.
Область решений неравенства 5x + y > 1 представляет собой полуплоскость выше линии, проходящей через точку С и далее вправо.
3) Найдем общую область решений:
Область решений системы неравенств представляет собой пересечение областей, полученных для каждого неравенства отдельно.
Итоговая область решений представляет собой многоугольник, ограниченный линиями, проходящими через точки А, В и С.








