Что значит найти корни многочлена

Многочлены являются основой алгебры и имеют широкое применение в различных областях науки, техники и экономики. Поиск корней многочлена – одна из основных задач, которая возникает при решении уравнений, моделировании и анализе данных. Зная корни многочлена, мы можем определить его свойства, построить его график и решить множество математических задач.

Корни многочлена – это значения переменной, при которых многочлен обращается в ноль. Нахождение корней многочлена может быть сложной задачей, особенно если многочлен имеет степень больше второй. Однако, существуют различные методы и алгоритмы, которые позволяют найти корни многочлена при помощи арифметических операций и итераций.

Один из самых популярных методов для поиска корней многочлена – метод Ньютона или метод касательной. Он основывается на принципе приближенного нахождения корня многочлена путем построения касательной к его графику и нахождения пересечения этой касательной с осью абсцисс. Данный метод позволяет достичь высокой точности в нахождении корней, однако требует начального приближения.

В дальнейшем мы рассмотрим дополнительные методы и техники для поиска корней многочлена, а также приведем примеры и практические задания, которые помогут вам лучше освоить эту важную тему. Нахождение корней многочлена – это не только математическое упражнение, но и навык, который может быть полезен в решении реальных проблем и задач в различных областях науки и техники.

Корни многочлена: что это и для чего нужно знать

Знание корней многочлена является важным для решения различных задач в математике. Например, зная корни многочлена, можно найти его максимумы и минимумы, точки перегиба, а также построить его график. Корни многочлена также позволяют решать уравнения и системы уравнений, связанные с этим многочленом.

Существует несколько методов для нахождения корней многочленов. Один из самых популярных методов – это метод подстановки. В этом методе мы подставляем различные значения для переменной многочлена и ищем такие значения, при которых многочлен обращается в нуль.

Другой метод для нахождения корней многочлена – это использование формулы Виета. Формула Виета позволяет найти сумму и произведение корней многочлена по его коэффициентам.

Знание корней многочлена позволяет более полно изучать свойства и особенности этого многочлена. Оно также является важным инструментом для решения различных математических задач и построения графиков функций.

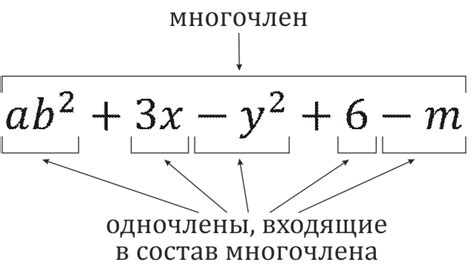
Многочлены: определение и примеры

Примеры многочленов:

• 3x+2 – это линейный многочлен, так как он содержит только одну переменную и степень этой переменной равна 1.

• 2x^2-5x+3 – это квадратичный многочлен, так как он содержит переменную в квадрате и степень этой переменной равна 2.

• 4x^3-2x^2+5x-1 – это кубический многочлен, так как он содержит переменную в кубе и степень этой переменной равна 3.

Старший коэффициент многочлена – это коэффициент при наивысшей степени переменной.

Как найти корни многочлена: основные методы

Существуют различные методы для нахождения корней многочленов. Некоторые из основных методов включают в себя:

1. Метод перебора
2. Метод деления с остатком
3. Метод Гаусса
4. Метод Ньютона

Метод перебора предполагает последовательную подстановку различных значений переменной в многочлен и проверку, является ли результат равным нулю. Этот метод применяется для поиска простых корней многочлена, но может быть неэффективен для многочленов более высоких степеней.

Метод деления с остатком основан на теореме Безу, которая устанавливает, что если числовое значение является корнем многочлена, то он делится на (x-a), где "a" - это значение корня. Этот метод позволяет находить корни многочлена путем последовательного деления и сокращения степени многочлена.

Метод Гаусса используется для решения систем линейных уравнений, в которых многочлены выражены в виде уравнений. Путем применения элементарных преобразований, система уравнений приводится к диагональному виду, где значения корней многочлена находятся на главной диагонали.

Метод Ньютона основан на итерационном процессе и предусматривает последовательное приближение корней многочлена. Этот метод требует знания некоторого начального приближения и использует производные многочлена для уточнения корней.

Выбор метода поиска корней многочлена зависит от его структуры, степени и возможности использования дополнительной информации. В некоторых случаях может потребоваться комбинация нескольких методов для нахождения всех корней многочлена.

Метод подстановки: шаги и примеры

Шаги метода подстановки:

1. Выбираем значение переменной и подставляем его в многочлен.
2. Решаем полученное уравнение и находим значение переменной.
3. Повторяем первые два шага для каждого значения переменной, пока не найдем все корни многочлена.

Пример:

Рассмотрим многочлен P(x) = 2x³ - 5x² + 3x - 6. Применим метод подстановки для нахождения корней этого многочлена.

1. Выберем значение переменной, например, x = 2.
2. Подставим значение переменной в многочлен: P(2) = 2*2³ - 5*2² + 3*2 - 6 = 16 - 20 + 6 - 6 = -4.
3. Уравнение P(x) = 0 не выполняется при x = 2.
4. Повторим шаги 1-3 для других значений переменной, например, x = 1. Подставим значение переменной в многочлен: P(1) = 2*1³ - 5*1² + 3*1 - 6 = 2 - 5 + 3 - 6 = -6.
5. Уравнение P(x) = 0 не выполняется при x = 1.
6. Повторим шаги 1-3 для следующего значения переменной, например, x = -1. Подставим значение переменной в многочлен: P(-1) = 2*(-1)³ - 5*(-1)² + 3*(-1) - 6 = -2 - 5 - 3 - 6 = -16.
7. Уравнение P(x) = 0 не выполняется при x = -1.
8. Повторим шаги 1-3 для последнего значения переменной, например, x = 3. Подставим значение переменной в многочлен: P(3) = 2*3³ - 5*3² + 3*3 - 6 = 54 - 45 + 9 - 6 = 12.
9. Уравнение P(x) = 0 не выполняется при x = 3.
10. Таким образом, метод подстановки не дал нам корней многочлена P(x) = 2x³ - 5x² + 3x - 6.

В данном примере метод подстановки не привел к нахождению корней многочлена, но в других случаях он может быть эффективным инструментом для решения уравнений.

Применение метода Виета для нахождения корней многочлена

Для многочлена степени n с коэффициентами a_n-1, a_n-2, ..., a₁, a₀, метод Виета утверждает, что сумма корней многочлена равна -a_n-1/a_n, а произведение корней равно (-1)ⁿ * a₀/a_n.

С помощью метода Виета можно упростить поиск корней многочлена. Вместо нахождения корней методом деления многочлена на линейный множитель, можно использовать заданные связи коэффициентов и вычислить сумму и произведение корней, которые затем могут быть использованы для определения самих корней.

Например, для многочлена x² - 5x + 6, сумма корней равна 5 / 1 = 5, а произведение корней равно 6 / 1 = 6. Используя эти связи, можно сделать выводы о корнях многочлена: корни должны быть двумя числами, сумма которых равна 5, а произведение равно 6. Таким образом, возможными корнями многочлена будут 2 и 3.

Метод деления синтетическим способом: шаг за шагом

Шаги по методу деления синтетическим способом:

1. Расположите коэффициенты многочлена в порядке убывания степеней.
2. Выберите подходящий делитель. Можно выбрать делитель, основываясь на корнях многочлена, данной в задаче информации или использовать метод подбора делителя.
3. Примените синтетическое деление, разделив первый коэффициент (который соответствует старшей степени) на делитель.
4. Умножьте делитель на частное полученного синтетического деления.
5. Расположите коэффициенты полученного многочлена после синтетического деления.
6. Проверьте остаток. Если остаток равен нулю, то делитель является корнем многочлена.
7. Повторяйте шаги 3-6, пока не получите многочлен с остатком, равным нулю или многочлен нельзя больше делить.

Пример применения метода деления синтетическим способом:

Дан многочлен 3x^3 - 4x^2 + 2x - 1. Найдем его корни.

Шаг 1: Расположим коэффициенты многочлена в порядке убывания степеней: 3, -4, 2, -1.

Шаг 2: Выберем делитель. Предположим, что x = 1 будет делителем.

Шаг 3: Применим синтетическое деление. Делим 3 на 1 и получаем 3.

Шаг 4: Умножаем делитель на частное синтетического деления. 1 * 3 = 3.

Шаг 5: Располагаем коэффициенты полученного многочлена после синтетического деления: -4, 2, -1 + 3.

Шаг 6: Проверяем остаток. Остаток равен -1 + 3 = 2.

Шаг 7: Поскольку остаток не равен нулю, повторяем шаги 3-6 с новым полученным многочленом.

Применяя метод деления синтетическим способом последовательно, мы найдем все корни многочлена.

Особенности нахождения корней многочленов высокой степени

Для многочлена высокой степени существует формула, позволяющая найти все его корни, которая называется "формулой Кардано". Однако применение этой формулы может быть затруднено, так как она требует решения кубического уравнения, что не всегда удобно и быстро.

В случаях, когда найти аналитическое решение многочлена высокой степени оказывается слишком сложно или невозможно, можно использовать численные методы, такие как метод Ньютона или метод деления отрезка пополам. Эти методы позволяют приближенно найти корни многочлена.

Также стоит отметить, что многочлены высокой степени могут иметь не только действительные корни, но и комплексные. Поэтому при решении задачи необходимо учитывать их возможное наличие и использовать соответствующие методы для их нахождения.

Значение корней многочлена и их графическое представление

Значение корней многочлена может быть как действительным, так и комплексным. Действительные корни многочлена представляются на числовой прямой, где каждому корню соответствует точка. Комплексные корни многочлена представляются в комплексной плоскости, где каждому комплексному корню соответствует точка.

Графическое представление корней многочлена позволяет лучше визуализировать их расположение и количество. Анализ графика позволяет найти интервалы, на которых многочлен принимает положительные и отрицательные значения, а также определить количество корней многочлена.

Значение корней многочлена и их графическое представление очень важны для понимания свойств многочленов и решения различных задач, связанных с анализом и оптимизацией функций.