Математика - это наука о числах. В ее основе лежит изучение алгебры и геометрии, которые помогают нам понять и описать законы и свойства вселенной. В алгебре одним из ключевых понятий является многочлен. Многочлены используются в различных областях математики, физики и других точных наук.
Алгебраический многочлен может быть разложен на некоторый набор многочленов меньшей степени, называемых его делителями. Важным свойством многочлена является его приводимость или неприводимость. Многочлен называется неприводимым, если для него не существует такого разложения на более мелкие многочлены. Другими словами, неприводимый многочлен не может быть разложен на множители меньшей степени.
Пример: Рассмотрим многочлен вида \(f(x) = x^2 + 2x + 1\). Для него не существует таких многочленов \(g(x)\) и \(h(x)\), что \(f(x) = g(x) \cdot h(x)\) и степень обоих многочленов меньше степени \(f(x)\). Поэтому многочлен \(f(x)\) является неприводимым.
Неприводимые многочлены играют важную роль в алгебре и математике в целом. Они используются, например, в построении кодов для передачи информации и в криптографии. Поэтому их изучение имеет большое практическое значение для различных областей науки и техники.
Что такое неприводимый многочлен?

Неприводимый многочлен отличается от приводимого многочлена тем, что его невозможно разложить на произведение двух или более многочленов меньшей степени. Приводимый многочлен, напротив, может быть разложен на множители, которые также являются многочленами.
Особенность неприводимого многочлена заключается в его неразложимости на более простые составляющие. Это свойство делает неприводимые многочлены важными для построения различных алгебраических систем и решения уравнений.
Примером неприводимого многочлена может служить многочлен вида x^2 + 1, где x - переменная, а степень равна 2. Этот многочлен не может быть разложен на произведение двух многочленов меньшей степени и является неприводимым над множеством вещественных чисел.
Определение неприводимого многочлена
Многочлен называется приводимым, если он может быть представлен в виде произведения двух или более многочленов более низкой степени.
По определению, неприводимый многочлен не имеет нетривиальных делителей, то есть он не может быть разложен на произведение многочлена меньшей степени. Приводимый многочлен, наоборот, может быть разложен на многочлены меньшей степени с остатком.
Особенностью неприводимого многочлена является то, что он остается неприводимым, независимо от выбора поля коэффициентов. Это означает, что если многочлен является неприводимым над одним полем, то он будет неприводимым и над любым другим полем.
Особенности неприводимого многочлена
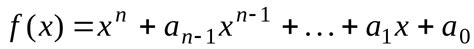
- Неприводимый многочлен не может быть разложен на линейные множители. В случае кольца многочленов над полем, это означает, что многочлен не имеет корней
- Если многочлен неприводим, то все его множители будут неприводимыми
- Неприводимые многочлены играют ключевую роль в построении расширений полей и в задачах связанных с алгебраическими числами
- Разложение многочлена на неприводимые множители является фундаментальным понятием алгебры и находит широкое применение в таких областях, как криптография, кодирование и теория ошибок
Примеры неприводимых многочленов
Неприводимые многочлены встречаются в различных областях математики и имеют важное значение в алгебре и теории чисел. Вот несколько примеров неприводимых многочленов:
- Многочлен x2 + 1 является неприводимым над полем вещественных чисел, так как не имеет корней.
- Многочлен x2 - 2 является неприводимым над рациональными числами. Это можно доказать, рассмотрев его корни: √2 и -√2.
- Многочлен x3 - 1 является неприводимым над полем комплексных чисел. В этом случае можно заметить, что он разлагается на линейные сомножители: (x - 1)(x - ei2π/3)(x - ei4π/3).
- Многочлен x4 + 4 также является неприводимым. Его нельзя разложить на множители с действительными коэффициентами.
Это лишь некоторые примеры неприводимых многочленов, и их существует бесконечное множество. Изучение их свойств и использование в различных математических областях помогает расширять понимание и применение алгебры и теории чисел.








