Что значит линейно зависимый вектор

Линейная алгебра - это раздел математики, который изучает линейные пространства и их свойства. Одним из важных понятий в линейной алгебре является понятие линейной зависимости векторов.

Вектор - это направленный отрезок, который имеет определенную длину и направление. Векторы можно складывать и умножать на скаляр, получая новые векторы. Для некоторых систем векторов можно установить, являются ли они линейно зависимыми или линейно независимыми.

Векторы называются линейно зависимыми, если существуют такие коэффициенты, при которых их линейная комбинация равна нулевому вектору. Если ни одна линейная комбинация векторов не равна нулевому вектору, то векторы считаются линейно независимыми.

Определение линейной зависимости векторов формулируется следующим образом: система векторов (v1, v2, ..., vn) называется линейно зависимой, если существуют не все нулевые коэффициенты a1, a2, ..., an, такие, что a1v1 + a2v2 + ... + anvn = 0.

Определение линейной зависимости векторов

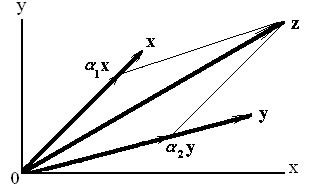
В линейной алгебре векторы называются линейно зависимыми, если существуют такие их коэффициенты, не все из которых равны нулю, что их линейная комбинация равна нулевому вектору.

Формально, векторы a₁, a₂,...,a_n называются линейно зависимыми, если существуют коэффициенты c₁, c₂,...,c_n, не все из которых равны нулю, такие что:

c₁a₁ + c₂a₂ + ... + c_na_n = 0

Если же таких коэффициентов не существует, то векторы считаются линейно независимыми.

Понятие линейной зависимости векторов широко используется во многих областях математики, физики и компьютерных наук, включая анализ данных, обработку изображений и машинное обучение. Понимание этого понятия позволяет решать множество задач, связанных с анализом и манипуляцией векторами.

Понятие зависимости векторов

Формально, векторы v₁, v₂, ..., v_n называются линейно зависимыми, если существуют скаляры c₁, c₂, ..., c_n, не все равные нулю, такие что:

c₁v₁ + c₂v₂ + ... + c_nv_n = 0.

То есть, существует нетривиальная линейная комбинация векторов, равная нулевому вектору.

На практике, линейно зависимые векторы означают, что один из векторов можно выразить через другие. Например, если вектор v₁ = (1, 2, 3) и v₂ = (2, 4, 6), то v₂ является линейной комбинацией вектора v₁.

Отличие линейно зависимых векторов от линейно независимых заключается в том, что в первом случае существуют нетривиальные решения уравнения, их удовлетворяющие. В случае линейно независимых векторов, единственное решение будет тривиальным.

Определение линейной зависимости

Для определения линейной зависимости векторов, нужно проверить, существует ли ненулевое решение уравнения

где α₁, α₂, ..., αₙ - скаляры, v₁, v₂, ..., vₙ - векторы. Если существуют такие скаляры, что это уравнение выполняется, то векторы являются линейно зависимыми, в противном случае они называются линейно независимыми.

Если все скаляры α₁, α₂, ..., αₙ равны нулю, то это представление является тривиальным и векторы считаются линейно независимыми. Если же существуют ненулевые значения для α₁, α₂, ..., αₙ, то это представление является нетривиальным и векторы считаются линейно зависимыми.

Таким образом, чтобы определить линейную зависимость векторов, необходимо найти решения уравнения α₁v₁ + α₂v₂ + ... + αₙvₙ = 0, и если существует хотя бы одно нетривиальное решение, то векторы являются линейно зависимыми.

Критерии линейной зависимости векторов

Для определения линейной зависимости векторов нам потребуется использовать несколько критериев:

1. Если хотя бы один из векторов можно представить в виде линейной комбинации других векторов, то все эти векторы будут линейно зависимыми.
2. Если существует нетривиальное решение линейного уравнения

c₁v₁ + c₂v₂ + ... + c_nv_n = 0

где c₁, c₂, ..., c_n - не все равны нулю, то векторы v₁, v₂, ..., v_n являются линейно зависимыми.

3. Если ранг системы векторов меньше количества векторов, то они обязательно будут линейно зависимыми.
4. Если хотя бы один из векторов является линейной комбинацией других векторов, то система векторов будет линейно зависимой.

Знание и использование этих критериев позволяет эффективно определить линейную зависимость векторов и применить это в решении задач линейной алгебры.

Примеры линейно зависимых векторов

Рассмотрим несколько примеров:

1. Вектора (1, 2) и (2, 4):

Можно заметить, что вектор (2, 4) представляется в виде линейной комбинации вектора (1, 2) умноженного на 2. Таким образом, вектора (1, 2) и (2, 4) являются линейно зависимыми.

2. Вектора (1, 2) и (3, 4):

Невозможно представить один из векторов в виде линейной комбинации другого. Таким образом, вектора (1, 2) и (3, 4) являются линейно независимыми.

3. Вектора (3, 1), (-1, -3) и (2, -2):

Вектор (2, -2) представляется в виде линейной комбинации векторов (3, 1) и (-1, -3) с коэффициентами -1 и 1 соответственно. Таким образом, вектора (3, 1), (-1, -3) и (2, -2) являются линейно зависимыми.

Таким образом, примеры линейно зависимых векторов можно найти, анализируя их линейные комбинации и проверяя возможность представления одного вектора в виде суммы других векторов, умноженных на некоторые коэффициенты.