Замкнутость множества на сложение – одно из важнейших понятий в математике, которое описывает свойство множества сохранять свою структуру при выполнении операции сложения его элементов. Если множество является замкнутым на сложение, то результатом сложения любых двух его элементов также будет элемент данного множества.
Для понимания замкнутости множества на сложение рассмотрим примеры. Рассмотрим множество натуральных чисел ℚ. Это множество является замкнутым на сложение, так как результатом сложения любых двух натуральных чисел будет также натуральное число.
Например, 2 + 3 = 5, 4 + 6 = 10, 7 + 8 = 15 и т.д., где числа 2, 3, 4, 6, 7 и 8 являются элементами множества ℚ.
Другим примером замкнутого множества на сложение является множество целых чисел ℤ. В данном случае, результатом сложения любых двух целых чисел также будет целое число.
Определение замкнутости множества на сложение
Для наглядного примера рассмотрим множество положительных четных чисел. Это множество можно обозначить как:
A = {2, 4, 6, 8, ...}
Если мы возьмем любые два числа из данного множества и сложим их, например, 2 + 6, то получим число 8, которое также принадлежит множеству положительных четных чисел.
Таким образом, множество положительных четных чисел является замкнутым на сложение.
Примеры замкнутых множеств на сложение
Замкнутость множества на сложение означает, что если в множестве есть два элемента, то их сумма также принадлежит этому множеству. Рассмотрим несколько примеров замкнутых множеств на сложение:
1. Множество натуральных чисел (N):
Множество натуральных чисел состоит из положительных целых чисел, начиная с единицы. Это множество замкнуто на сложение, так как сумма двух натуральных чисел также будет натуральным числом. Например, 2 + 3 = 5, 4 + 6 = 10 и так далее. Таким образом, множество натуральных чисел является замкнутым на сложение.
2. Множество целых чисел (Z):
Множество целых чисел включает в себя все целые числа, как положительные, так и отрицательные. Это множество также является замкнутым на сложение, так как сумма двух целых чисел всегда будет целым числом. Например, 2 + (-3) = -1, (-4) + 6 = 2 и так далее.
3. Множество рациональных чисел (Q):
Множество рациональных чисел включает в себя все числа, которые можно представить в виде обыкновенной дроби (отношение двух целых чисел). Это множество также замкнуто на сложение, так как сумма двух рациональных чисел всегда будет рациональным числом. Например, 1/2 + 1/3 = 5/6, 2/5 + (-3/7) = -11/35 и так далее.
4. Множество действительных чисел (R):
Множество действительных чисел включает в себя все числа, в том числе и иррациональные (которые не могут быть представлены в виде обыкновенной дроби). Это множество также является замкнутым на сложение, так как сумма двух действительных чисел всегда будет действительным числом. Например, 2.5 + (-1.3) = 1.2, 0.4 + π = π + 0.4 и так далее.
Таким образом, все вышеперечисленные множества являются замкнутыми на сложение, то есть сумма любых двух элементов из этих множеств также принадлежит этим множествам.
Множество натуральных чисел

Множество натуральных чисел обозначается как N и содержит все положительные целые числа, начиная с единицы. Если записать множество натуральных чисел в упорядоченном виде, то получится следующая последовательность: 1, 2, 3, 4, 5, ...
Множество натуральных чисел является замкнутым относительно операции сложения, что означает, что результатом сложения двух натуральных чисел будет также натуральное число. Например, если взять два произвольных числа из множества натуральных чисел, например, 3 и 5, и сложить их, то получится число 8, которое также является натуральным числом.
Также множество натуральных чисел является замкнутым относительно операции вычитания, что означает, что результатом вычитания двух натуральных чисел будет также натуральное число, если результат неотрицательный. Например, если взять два числа из множества натуральных чисел, например, 8 и 3, и вычесть из них 5, то получится число 3, которое также является натуральным числом.
Таким образом, множество натуральных чисел является замкнутым на сложение и вычитание.
Множество целых чисел
Множество целых чисел обозначается символом ℤ и состоит из положительных, отрицательных и нулевых целых чисел, а также их комбинаций.
Примеры элементов множества целых чисел:
- 1
- -2
- 0
- 100
- -500
Множество целых чисел также является замкнутым на вычитание, умножение и деление, что означает, что результаты этих операций также будут принадлежать множеству целых чисел.
Множество рациональных чисел
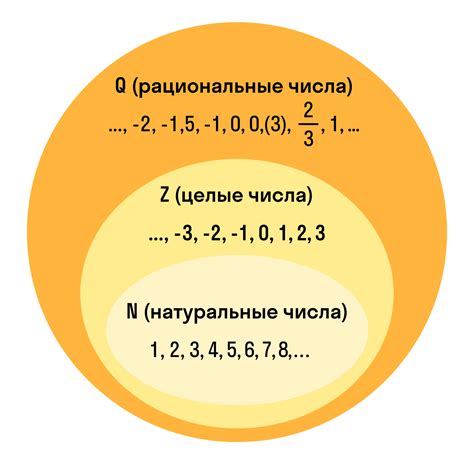
Примеры рациональных чисел включают в себя целые числа, десятичные дроби и конечные десятичные числа. Например, числа 2, -5, 0, 0.5, 1.25 являются рациональными числами.
Можно представить рациональные числа как бесконечные десятичные дроби, такие как 0.333..., которая эквивалентна числу 1/3. Рациональные числа также могут быть представлены в виде конечных десятичных дробей, например 0.25, которая эквивалентна числу 1/4.
Множество рациональных чисел замкнуто относительно сложения, что означает, что сумма двух рациональных чисел также является рациональным числом. Например, если и являются рациональными числами, то также будет рациональным числом.
Множество рациональных чисел является подмножеством множества вещественных чисел , которые включают в себя все рациональные числа, а также иррациональные числа, которые не могут быть представлены в виде дроби и имеют бесконечную десятичную запись без повторяющихся цифр.
Множество действительных чисел
Это означает, что если взять два произвольных числа из этого множества, их сумма также будет принадлежать множеству действительных чисел. Например, если взять два целых числа из ℝ, например 2 и 5, и их сложить, получится число 7, которое также принадлежит множеству действительных чисел.
Также множество действительных чисел включает в себя дробные числа, такие как 1/2 или 3.14. Если взять два дробных числа из ℝ, их сумма также будет действительным числом. Например, если взять 1/3 и 4/7, их сумма составит 23/21, которое также принадлежит множеству действительных чисел.
Иррациональные числа, такие как π (число пи) или √2 (квадратный корень из 2), также принадлежат множеству действительных чисел. Если взять два иррациональных числа из ℝ, их сумма будет являться другим иррациональным числом.
Таким образом, множество действительных чисел является замкнутым на сложение множеством, наиболее общим для большинства математических операций.
Множество комплексных чисел

В множестве комплексных чисел можно выполнять операции сложения, вычитания, умножения и деления.
Например, если у нас есть два комплексных числа z1=a1+b1i и z2=a2+b2i, то их сумма z1+z2=(a1+a2)+(b1+b2)i, а разность z1-z2=(a1-a2)+(b1-b2)i.
Умножение комплексных чисел осуществляется по формуле: (a1+b1i)*(a2+b2i)=(a1a2-b1b2)+(a1b2+a2b1)i.
Также, если z1 и z2 - не равны нулю, то их частное (деление) z1/z2=(a1a2+b1b2)/(a2^2+b2^2)+((a2b1-a1b2)/(a2^2+b2^2)).
Множество комплексных чисел C является замкнутым на сложение, так как сумма двух комплексных чисел также является комплексным числом.
| Примеры комплексных чисел | Действительная часть (a) | Мнимая часть (b) |
|---|---|---|
| i | 0 | 1 |
| 3+2i | 3 | 2 |
| -5-7i | -5 | -7 |
| 4i | 0 | 4 |
| 1 | 1 | 0 |
Выводы и применение замкнутости множеств на сложение
Замкнутость множества на сложение широко применяется в различных областях, включая математику, физику, экономику и информатику.
В математике замкнутость множества на сложение является одним из основных свойств алгебраических структур, таких как поле или кольцо. Она позволяет доказывать различные теоремы, изучать свойства и сравнивать различные множества чисел.
В физике замкнутость множества на сложение используется при решении задач, связанных с комбинированием различных физических величин. Например, при сложении скоростей или сил, замкнутость множества на сложение позволяет получить корректные результаты и описать движение или взаимодействие объектов.
В экономике замкнутость множества на сложение применяется при анализе денежных потоков и расчете общей стоимости товаров и услуг. Замкнутость множества на сложение позволяет проводить точные и надежные расчеты и предсказывать экономические последствия различных операций и событий.
В информатике замкнутость множества на сложение широко используется в алгоритмах и программировании. Например, при работе с массивами или списками чисел, замкнутость множества на сложение гарантирует корректность операций и выполняемых алгоритмов, а также позволяет эффективно выполнять различные вычисления и обработку данных.
Таким образом, замкнутость множества на сложение является важным свойством и имеет широкое применение в различных областях. Она обеспечивает надежность и корректность операций, позволяет проводить анализ и исследование числовых структур, а также разрабатывать эффективные алгоритмы и программы.








