В математическом анализе стационарные точки функции играют важную роль при изучении ее свойств и поведения. Стационарные точки – это точки, в которых производная функции равна нулю или не существует. Они могут быть локальными минимумами, максимумами или точками перегиба функции.
Значение стационарных точек функции позволяет нам определить ее критические точки, то есть места, где функция может иметь особые свойства или изменять свое поведение. Анализ критических точек позволяет нам определить экстремумы функции и различные виды точек перегиба.
Кроме того, стационарные точки могут быть связаны с другими интересными свойствами функции, такими как асимптоты, симметричность и периодичность. Они являются ключевыми точками, в которых функция может переходить из одного состояния в другое или иметь особенности своей формы.
Исследование стационарных точек функции требует тщательного анализа и использования различных методов математического анализа, таких как нахождение производных, составление таблицы знаков, применение теоремы Ролля и других.
В итоге, изучение стационарных точек функции позволяет нам получить более глубокое понимание ее свойств и поведения, а также применить это знание в решении различных задач и проблем в различных областях науки и техники.
Определение стационарной точки
Существуют два основных типа стационарных точек - экстремумы и точки перегиба. Экстремумы делятся на два типа: максимумы и минимумы. В точке максимума функция достигает наибольшего значения, а в точке минимума - наименьшего значения.
Стационарные точки часто используются для определения глобальных этих экстремумов функции. Если функция имеет одну или несколько стационарных точек, то анализируя значения функции в этих точках и на границах области определения функции, можно найти глобальные экстремумы.
Кроме того, стационарные точки играют важную роль в определении кривизны графика функции. Например, точки перегиба функции - это стационарные точки, где меняется конкавность графика функции.
Таким образом, стационарные точки являются ключевыми точками при анализе функций и позволяют определить глобальные экстремумы и характер изменения графика функции.
Значение стационарных точек в анализе функций
Знание стационарных точек функции позволяет нам выяснить ее основные характеристики. Например, стационарная точка может быть локальным минимумом, локальным максимумом или точкой перегиба функции.
Для определения типа стационарной точки необходимо анализировать производную функции в окрестности этой точки. Если производная меняет знак с плюса на минус, то это локальный максимум. Если производная меняет знак с минуса на плюс, то это локальный минимум. Если производная не меняет знак, то это точка перегиба.
Изучение стационарных точек позволяет нам также находить экстремумы функции. Зная координаты стационарной точки, можно определить значения функции в этой точке и сравнить их с значениями в других точках. Таким образом, стационарные точки помогают нам находить самые минимальные и максимальные значения функции.
Также стационарные точки играют важную роль в оптимизации задач. Часто задача заключается в нахождении максимального или минимального значения функции при определенных ограничениях. Используя анализ стационарных точек, можно оптимизировать значения функции, выбрав такие значения переменных, при которых достигается экстремум.
В целом, стационарные точки являются полезным инструментом в анализе функций, позволяющим нам определить их основные характеристики, находить экстремумы и оптимизировать задачи.
| Исходная функция | Производная функции | Тип стационарной точки |
|---|---|---|
| f(x) = x^2 - 4x + 3 | f'(x) = 2x - 4 | Локальный минимум |
Роль стационарных точек в оптимизации
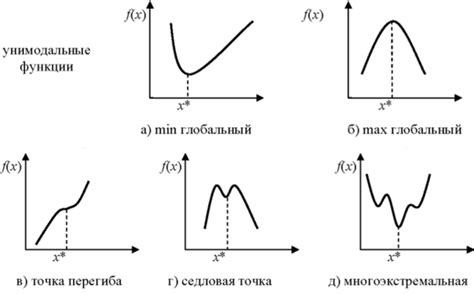
Стационарные точки являются точками, в которых производная функции равна нулю или не существует. Они могут быть минимумами, максимумами или седловыми точками. Минимумы - это точки, в которых функция принимает наименьшее значение, максимумы - точки, в которых функция принимает наибольшее значение, а седловые точки - это точки, в которых функция имеет экстремум по одной из координат и точку перегиба по другой координате.
Найдя стационарные точки функции, мы можем использовать различные методы оптимизации для определения значения функции в этих точках. Один из таких методов - градиентный спуск. Градиентный спуск позволяет найти локальные минимумы и максимумы функции, двигаясь в направлении, обратном градиенту функции. Этот метод основан на свойствах стационарных точек функции. Также существуют и другие методы оптимизации, которые используют стационарные точки.
Важно отметить, что стационарные точки не всегда являются оптимальными решениями. В некоторых случаях, функция может иметь множество стационарных точек, в которых функция принимает одно и то же значение. В таких случаях необходимо использовать дополнительные методы оптимизации для выбора наилучшего решения.
Таким образом, стационарные точки функции играют важную роль в оптимизации, позволяя найти максимумы и минимумы функции и определить оптимальное значение. Использование стационарных точек и методов оптимизации помогает обработке данных и принятию решений на основе математического анализа и статистики.
Связь стационарных точек с производными функций
Если функция имеет стационарную точку, то производная функции в этой точке равна нулю или не существует. Это может быть полезной информацией при изучении поведения функции в окружении стационарной точки. Например, знание производных функций может помочь определить, какие точки являются минимумами, максимумами или перегибами функции.
Кроме того, связь между стационарными точками и производными функций позволяет нам найти стационарные точки функции, опираясь только на производные функции. Например, если мы не можем найти точку, в которой производная функции равна нулю, можем найти точки, в которых производная функции меняет знак. Эти точки могут быть потенциальными стационарными точками функции.
Таким образом, связь стационарных точек с производными функций является важным инструментом в анализе функций. Она позволяет нам находить стационарные точки, изучать поведение функции около этих точек и определять экстремумы и перегибы функции.
Примеры использования стационарных точек в математическом анализе
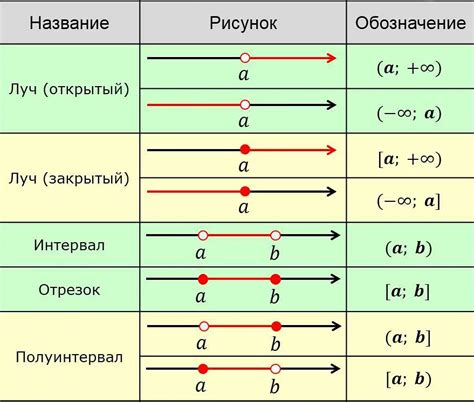
Стационарные точки функции, такие как минимумы, максимумы и точки перегиба, имеют важное значение в математическом анализе. Они помогают нам понять поведение функции, определить ее экстремумы и найти интересные точки на графике функции.
Одним из наиболее распространенных примеров использования стационарных точек является нахождение максимумов и минимумов функций. Для этого анализируются производные функции и их стационарные точки. Если значение первой производной равно нулю и вторая производная отлична от нуля, то это указывает на наличие экстремума в данной точке. Таким образом, стационарные точки помогают определить местоположение и значения экстремумов функции.
Другим примером использования стационарных точек является исследование точек перегиба функций. Точка перегиба - это точка на графике функции, в которой происходит изменение кривизны. Для определения точек перегиба анализируются производные высших порядков функции. Если вторая производная равна нулю и третья производная не равна нулю, то это указывает на наличие точки перегиба. Стационарные точки позволяют нам понять, где происходят смены кривизны и как изменяется график функции.
Кроме того, стационарные точки могут быть использованы для определения критических значений функции. Критические значения - это значения функции, в которых первая производная равна нулю или не существует. Это могут быть экстремумы функции или точки перегиба. Зная критические значения, мы можем определить интересные точки функции и изучить их свойства.
Таким образом, стационарные точки играют важную роль в математическом анализе, помогая нам понять свойства функций, определить экстремумы и точки перегиба, а также найти интересные значения функции. Использование стационарных точек позволяет нам более глубоко исследовать функции и получить более полное представление о их характеристиках.
Практическое применение стационарных точек
Стационарные точки функции играют важную роль в анализе и оптимизации различных процессов. Они позволяют определить экстремумы функции, которые могут быть максимальными или минимальными значениями. Это особенно полезно в задачах, связанных с оптимизацией ресурсов или поиском оптимальных решений.
Например, в экономике стационарные точки используются для определения оптимальных цен на товары или услуги, максимизации прибыли или минимизации затрат. Анализ стационарных точек помогает найти такие значения переменных, при которых достигается оптимальное соотношение между затратами и доходами.
В физике стационарные точки позволяют определить положение равновесия системы. Это важно при изучении колебаний, стабильности или устойчивости различных физических процессов. Также стационарные точки используются в оптимизации технических систем для достижения максимальной эффективности или минимизации потерь.
В машинном обучении стационарные точки помогают находить оптимальные параметры моделей, при которых достигается наилучшее качество предсказаний. Это важно при обучении нейронных сетей, регрессии, классификации или кластеризации данных.
На практике стационарные точки применяются во многих областях, где требуется анализ или оптимизация функций. Они позволяют найти оптимальные решения, принять взвешенные решения или лучше понять поведение системы. Поэтому понимание стационарных точек и их использование в анализе является важным навыком для специалиста в различных областях знаний.
Позитивные и негативные аспекты стационарных точек

Один из позитивных аспектов стационарных точек - это возможность определения экстремумов функции. Если стационарная точка является локальным минимумом или максимумом, то она позволяет нам найти точки на графике функции, где значение функции достигает минимума или максимума. Это может быть полезно, например, при оптимизации процессов или при решении задач математического программирования.
Однако стационарные точки могут иметь и негативные аспекты. Например, стационарные точки, которые не являются экстремумами, могут быть точками перегиба функции. В этих точках функция меняет свой характер и переходит из убывающей, например, в возрастающую и наоборот. Такие точки могут оказаться неудобными в дальнейшем анализе функции, так как они усложняют построение ее графика и понимание ее поведения.
Еще одним негативным аспектом стационарных точек является их присутствие в функциях, которые не имеют глобального экстремума. Например, в неограниченных функциях может быть множество стационарных точек, но ни одна из них не является глобальным минимумом или максимумом функции. Это может привести к неверной интерпретации результатов, если мы ищем глобальный экстремум исследуемой функции.
| Позитивные аспекты | Негативные аспекты |
|---|---|
| Помогают определить экстремумы функции | Могут быть точками перегиба функции |
| - | Могут присутствовать в функциях без глобального экстремума |








