Проекция - это понятие, которое активно используется в геометрии для описания взаимного расположения геометрических фигур. Проекция катета является одним из важных понятий в геометрии треугольников, которое позволяет определить, каким образом данный катет проецируется на другой объект или плоскость.
Определение проекции катета просто: это длина отрезка, который получается в результате проекции данного катета на перпендикулярную ему плоскость. Другими словами, проекция катета - это отличие между длиной самого катета и его проекции на плоскость.
Понимание проекции катета важно при решении задач, связанных с треугольниками, так как позволяет определить расстояние от катета до плоскости, на которую он проецируется. Кроме того, проекция катета является основой для определения других понятий, таких как гипотенуза и площадь треугольника.
Что такое проекция катета и как она определяется?
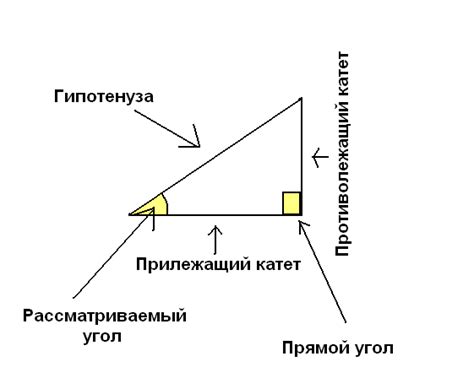
Проекция катета определяется с помощью подобия треугольников. Если в прямоугольном треугольнике один из его катетов является основанием, а противолежащий катет - высотой, то проекцией высоты на основание будет катет, соответствующий основанию. Он параллелен данной высоте и имеет такую же длину.
Проекция катета используется при решении задач, связанных с вычислением длины сторон прямоугольного треугольника. Кроме того, проекция катета позволяет вывести формулу для определения площади прямоугольного треугольника через длину его катетов и гипотенузу.
Итак, проекция катета - это отрезок, полученный проецированием катета прямоугольного треугольника на его гипотенузу. Она определяется с помощью подобия треугольников и используется для решения задач по вычислению длины сторон и площади прямоугольного треугольника.
Понятие проекции катета
Определение проекции катета можно представить следующим образом:
Пусть АВ – катет прямоугольного треугольника, а АС – проекция этого катета на гипотенузу.
Проекция катета определяется как отрезок, длина которого равна произведению длины катета на косинус угла между гипотенузой и катетом:
АС = АВ · cos(α), где АВ – длина катета, α – угол между гипотенузой и катетом.
Таким образом, проекция катета позволяет определить длину и положение отрезка, образованного катетом и его проекцией на гипотенузу.
Определение проекции катета
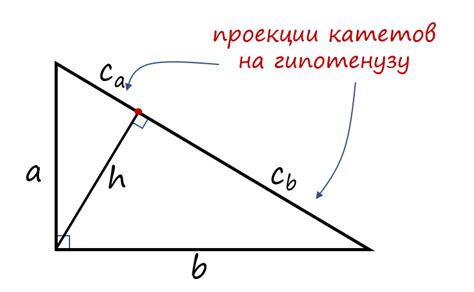
Проекция катета может быть положительной или отрицательной, в зависимости от направления оси или плоскости, на которую проецируется катет. Если ось или плоскость направлена вперед (в положительном направлении), проекция катета будет положительной. Если ось или плоскость направлена назад (в отрицательном направлении), проекция катета будет отрицательной.
Проекция катета может быть определена с использованием теоремы Пифагора и тригонометрических функций, таких как синус и косинус. В зависимости от конкретной задачи или контекста, проекция катета может быть использована для расчета других параметров или характеристик, таких как высота, расстояние или угол.
Виды проекции катета
Существует несколько видов проекции катета:
- Вертикальная проекция катета - проекция, которая определяется перпендикулярной линией, проведенной от начала координат к катету, параллельному оси y.
- Горизонтальная проекция катета - проекция, которая определяется перпендикулярной линией, проведенной от начала координат к катету, параллельному оси x.
- Диагональная проекция катета - проекция, которая определяется перпендикулярной линией, проведенной от начала координат к катету, образующему угол под острым углом с одной из осей координат.
Вид проекции катета зависит от ориентации катета относительно осей координат. Каждый вид проекции катета имеет свои особенности и может использоваться в различных областях, таких как геометрия, физика и инженерия.
Значение проекции катета в геометрии

Проекция катета используется для нахождения длины этого катета, если известны длина гипотенузы и угол между гипотенузой и проекцией катета. Также проекция катета может использоваться для нахождения площади треугольника, если известны длина гипотенузы и длина катета.
Понимание понятия проекции катета позволяет применять его в различных геометрических задачах, таких как нахождение высоты треугольника, построение треугольника по условиям и т.д.
Проекция катета имеет важное значение в геометрии и широко применяется для решения задач, связанных с треугольниками. Понимание этого понятия помогает упростить и точнее выполнить геометрические вычисления и построения.
Проекция катета в прямоугольном треугольнике
Для определения проекции катета используется теорема Пифагора, которая устанавливает соотношение между длинами катетов и гипотенузы в прямоугольном треугольнике:
| Катет A: | Гипотенуза: | Проекция: |
| a | c | h |
Для вычисления проекции катета применяется теорема Пифагора в виде следующего соотношения:
h = sqrt(c^2 - a^2)
где a - длина катета, c - длина гипотенузы, h - длина проекции.
Проекция катета является полезной величиной при решении различных геометрических задач, в том числе при нахождении высоты, площади и объема прямоугольного треугольника.
Проекция катета и его визуальное представление

Для визуального представления проекции катета можно провести линию, перпендикулярную плоскости проекций, и найти точку ее пересечения с этой плоскостью. Полученная точка будет являться проекцией катета на данную плоскость.
Проекция катета может быть положительной или отрицательной в зависимости от направления линии проекции. Положительная проекция свидетельствует о том, что объект находится перед плоскостью проекции, а отрицательная проекция указывает на то, что объект находится позади плоскости проекции.
Использование проекции катета позволяет упростить анализ геометрических объектов и проведение измерений на плоскости проекций. Она широко применяется в различных областях, включая геодезию, строительство, архитектуру и механику.
Формула расчета проекции катета
Чтобы определить длину проекции катета, необходимо знать длину самого катета и угол между катетом и основанием треугольника.
Формула для расчета проекции катета выглядит следующим образом:
длина проекции катета = длина катета * cos(угол)
Где:
- длина проекции катета - значение, которое нужно найти;
- длина катета - известная длина катета прямоугольного треугольника;
- угол - угол между катетом и основанием треугольника, заданный в радианах.
Вычисление проекции катета с помощью данной формулы позволяет определить длину проекции без необходимости измерения самой проекции.
Проекция катета в практических примерах

Рассмотрим несколько практических примеров для лучшего понимания этого понятия.
Пример 1: Пусть у нас есть прямоугольный треугольник с катетами длиной 3 и 4. Нам нужно найти проекцию более короткого катета (катета длиной 3) на главную диагональ треугольника, которая является осью проекции.
Проекция катета может быть найдена с использованием формулы:
Проекция = Катет × cos(Угол между Катетом и Осью)
Угол между катетом и осью, в данном случае главной диагональю, составляет 90 градусов. Подставим значения в формулу:
Проекция = 3 × cos(90°) = 3 × 0 = 0
Таким образом, проекция катета длиной 3 на главную диагональ треугольника равна 0.
Пример 2: Предположим, что у нас есть прямоугольное здание с длиной и шириной 20 и 30 метров соответственно. Нам нужно найти проекцию длины (катета) здания на землю, которая является горизонтальной осью.
Угол между длиной здания и горизонтальной осью составляет 90 градусов. Подставим значения в формулу:
Проекция = 20 × cos(90°) = 20 × 0 = 0
Таким образом, проекция длины здания на землю равна 0.
В данных примерах видно, что проекция катета может быть нулевой, если угол между катетом и осью равен 90 градусам. В противном случае, проекция будет иметь ненулевое значение, которое зависит от длины катета и угла.








