Правильная треугольная пирамида – это геометрическое тело, которое образуется, если плоскость разбита на равносторонние треугольники и все они сходятся в одной точке – вершине пирамиды. Таким образом, каждая грань пирамиды является равносторонним треугольником, а вершина – единственной точкой пересечения всех его высот. Правильная треугольная пирамида является одним из примеров правильных многогранников, которые имеют одинаковые стороны и углы.
Свойства правильной треугольной пирамиды включают в себя:
1. Равносторонние треугольники: Все грани пирамиды являются равносторонними треугольниками. Это значит, что все их стороны равны друг другу и все углы между сторонами равны 60 градусов.
2. Единственная вершина: У правильной треугольной пирамиды есть единственная вершина, где все грани пирамиды сходятся. Вершина является точкой пересечения всех высот пирамиды.
3. Правильные ребра: Ребра правильной треугольной пирамиды также равны друг другу. Все ребра имеют одинаковую длину и соединяют вершину пирамиды с центрами сторон ее граней.
Примеры правильной треугольной пирамиды включают пирамиду на шляпе египетской царицы Нефертити, пирамиды Майя в Мексике и пирамиду на заднем дворе жителя, собравшегося построить правильную треугольную пирамиду из стаканов. Эти примеры демонстрируют, как правильная треугольная пирамида обнаруживается в разных аспектах жизни и искусства.
Что такое правильная треугольная пирамида?
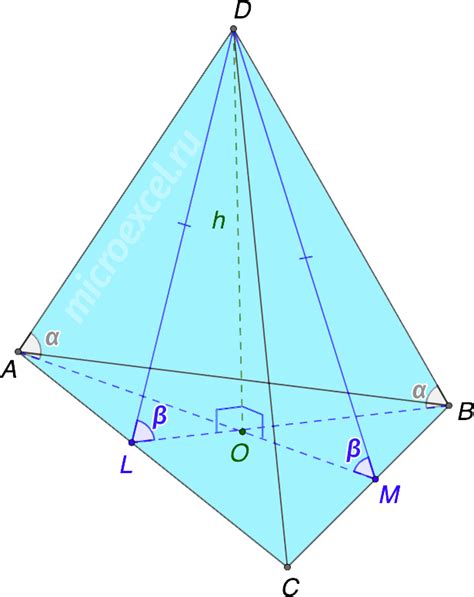
У правильной треугольной пирамиды есть несколько основных свойств:
| Основание | Треугольная плоскость, на которой стоят все вершины пирамиды. |
| Высота | Отрезок, соединяющий вершину пирамиды с центром основания, перпендикулярный плоскости основания. |
| Ребро | Отрезок, соединяющий вершину пирамиды с одной из вершин основания. |
| Угол между гранями | Угол между любыми двумя гранями пирамиды равен 60 градусам. |
| Объем | Объем правильной треугольной пирамиды можно вычислить по формуле V = (1/3) * A * h, где A - площадь основания, h - высота. |
| Площадь поверхности | Площадь поверхности правильной треугольной пирамиды можно вычислить по формуле P = A + (3/2) * a * l, где A - площадь основания, a - длина ребра, l - длина боковых граней. |
Примером правильной треугольной пирамиды может служить пирамида Хеопса в Гизе, Египет. Она имеет равностороннюю треугольную основу и четыре равносторонние боковые грани.
Определение
Основные свойства правильной треугольной пирамиды
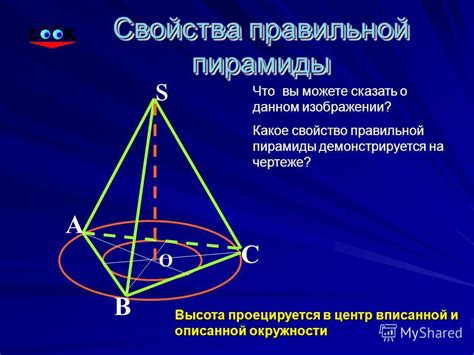
Основные свойства правильной треугольной пирамиды:
- Равносторонний треугольник. Основание пирамиды представляет собой равносторонний треугольник, у которого все стороны и углы равны между собой.
- Равные боковые грани. Все боковые грани пирамиды равны между собой и имеют форму равносторонних треугольников.
- Ребра и высота. В пирамиде все ребра равны между собой, а высота пирамиды проходит от вершины до центра основания и является перпендикулярной аналогичной стороне основания.
- Симметрия. Правильная треугольная пирамида обладает симметричной структурой, все боковые грани являются подобными треугольниками, и симметричны относительно оси, проходящей через вершину пирамиды и центр основания.
- Объем и площадь. Объем правильной треугольной пирамиды можно вычислить по формуле V = (1/3) * A * h, где A - площадь основания, h - высота пирамиды. Площадь основания можно вычислить по формуле S = (a^2 * sqrt(3)) / 4, где a - длина стороны основания.
Примерами правильной треугольной пирамиды являются пирамиды, имеющие правильные треугольники в качестве основания, например пирамида Хеопса в Гизе или пирамида Серпинского.
Примеры
Вот некоторые примеры правильных треугольных пирамид:
- Пирамида с основанием, состоящим из трех равносторонних треугольников.
- Пирамида с основанием, состоящим из трех равнобедренных треугольников.
- Пирамида с основанием, состоящим из трех прямоугольных треугольников.
- Пирамида с основанием, состоящим из трех разносторонних треугольников.
Каждая из этих пирамид имеет треугольную основу и все грани являются равнобедренными треугольниками. Они также обладают свойствами правильных треугольных пирамид, описанными ранее.
Пример 1: Правильная треугольная пирамида в геометрии
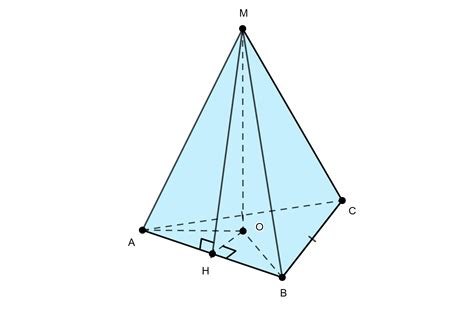
| Свойства правильной треугольной пирамиды |
|---|
| Все грани являются равносторонними треугольниками |
| Все боковые грани равны между собой |
| Угол между двумя боковыми гранями равен 60 градусов |
| Площадь основания может быть вычислена по формуле: S = (a^2 * √3) / 4, где "a" - длина стороны основания |
| Объём пирамиды может быть вычислен по формуле: V = (a^2 * h * √2) / 12, где "a" - длина стороны основания, "h" - высота пирамиды |
Примером правильной треугольной пирамиды может служить пирамида Кеопса, одна из самых известных старинных пирамид в мире. Она имеет равностороннюю треугольную основу и четыре равносторонние боковые грани, которые сходятся в её вершине.
Пример 2: Правильная треугольная пирамида в прикладных науках
Правильная треугольная пирамида широко применяется в различных областях прикладных наук. Например, в геометрии такая пирамида используется для создания моделей трехмерных объектов.
В архитектуре правильные треугольные пирамиды могут использоваться как структурные элементы в строительстве, обеспечивая прочность и устойчивость зданий.
Также правильные треугольные пирамиды применяются в химии и физике. В химии они могут служить моделями молекул и реакций, так как трехмерная форма пирамиды помогает наглядно представить взаимное расположение атомов. В физике правильные треугольные пирамиды могут быть использованы в оптике для создания моделей линз и преломляющих элементов.
Также необходимо отметить, что правильные треугольные пирамиды имеют свои применения и в компьютерной графике. Они могут быть использованы для создания трехмерных моделей и анимации, так как они обладают особыми свойствами, такими как равные длины ребер и углов.








