В математическом анализе конечный предел является одним из основных понятий, которое позволяет определить поведение функции при приближении ее аргумента к определенной точке. Это понятие играет ключевую роль в понимании процессов в физике, экономике и других науках.
Конечный предел функции f(x) при x, стремящемся к заданной точке a, записывается в виде lim(x->a) f(x) = L, где L - конечное число. Если при приближении аргумента к точке a значение функции f(x) стремится к конечному числу L, то говорят, что у функции существует конечный предел в точке a.
Примером функции с конечным пределом может служить f(x) = 1/x. В данном случае, при x, стремящемся к бесконечности или минус бесконечности, значение функции f(x) стремится к нулю. То есть, lim(x->∞) (1/x) = 0. Это означает, что при возрастании аргумента функции до бесконечности, значение функции уменьшается и приближается к нулю.
Использование понятия конечного предела позволяет определить поведение функции в окрестности точки, в которой предел рассматривается, и описать асимптотическое поведение функции при стремлении аргумента к этой точке.
Что такое конечный предел

В математике конечный предел представляет собой число, к которому последовательность или функция стремится, когда их аргумент приближается к какому-либо значению. Он показывает, что значение последовательности или функции стабилизируется или "стремится" к конкретному значению.
Конечный предел может быть полезен во многих областях математики, физики, экономики и других науках для изучения изменений и поведения функций или переменных. Он позволяет определить, куда и как быстро сходится последовательность или функция, а также предсказывать результаты исследований.
Например:
Пусть дана функция f(x) = 2x + 1. Конечным пределом этой функции при x, стремящемся к 3, будет число 7. Определение конечного предела говорит нам, что функция будет стремиться к значению 7, когда x будет приближаться к 3.
Понятие предела последовательности
Последовательность – это упорядоченный набор чисел, причём для каждого натурального числа существует соответствующий элемент последовательности.
Предел последовательности обозначается следующим образом: lim n → ∞ an = L, где an – элементы последовательности, n – номер элемента, L – предел.
Если при росте n элементы последовательности an стремятся к числу L, то L называется пределом последовательности, а последовательность называется сходящейся. В противном случае последовательность называется расходящейся.
Например, последовательность an = 1/n будет сходящейся, так как при увеличении n элементы последовательности стремятся к нулю: lim n → ∞ 1/n = 0. Также, последовательность bn = n будет расходящейся, так как при увеличении n элементы последовательности стремятся к бесконечности: lim n → ∞ n = ∞.
Определение конечного предела
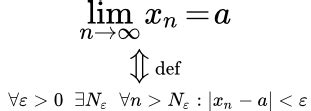
Для функции f(x) и числа a конечный предел обозначается следующим образом:
lim(x→a) f(x) = L,
где L – конечное число. Это означает, что при приближении значения переменной x к точке a значения функции f(x) приближаются к числу L.
Для последовательности чисел {a_n} конечный предел обозначается следующим образом:
lim(n→∞) a_n = L,
где L – конечное число. Это означает, что при стремлении номера элемента n к бесконечности значения элементов последовательности a_n приближаются к числу L.
Определение конечного предела позволяет изучать асимптотическое исследование функций и последовательностей, а также решать множество задач в математике и физике.
Пример:
Рассмотрим функцию f(x) = 1/x при x ≠ 0. Найдем ее предел при x, стремящемся к нулю.
lim(x→0) 1/x = ∞,
так как при приближении значения переменной x к нулю значения функции f(x) увеличиваются бесконечно.
Сходимость и разносторонний конечный предел
Когда мы говорим о сходимости последовательности, мы имеем в виду, что элементы этой последовательности приближаются друг к другу или к определенному значению по мере продвижения в бесконечность. Однако бывают случаи, когда предел последовательности может быть нестандартным или разносторонним.
Разносторонний конечный предел возникает, когда предельное значение последовательности существует, но не является бесконечным. Это означает, что элементы последовательности приближаются к предельному значению, но никогда не достигают его. Например, последовательность 1, 1/2, 1/3, 1/4, ... сходится к разностороннему пределу 0.
Если последовательность имеет разносторонний конечный предел, то можно сказать, что она неограничена. Другими словами, существует бесконечное количество элементов последовательности, которые находятся ближе к предельному значению, чем любое фиксированное число.
Разносторонний конечный предел может быть полезен при решении математических задач, особенно в тех случаях, когда предельное значение является недосягаемым, но все же имеет определенное значение.
В целом, конечный предел последовательности может быть стандартным или разносторонним. Стандартный конечный предел достигается, когда элементы последовательности приближаются и, в конечном итоге, равны предельному значению. Разносторонний конечный предел достигается, когда элементы последовательности приближаются к предельному значению, но никогда его не достигают.
Пример 1: Конечный предел при увеличении значения переменной

Рассмотрим функцию f(x) = \frac{1}{x}. Чтобы найти конечный предел этой функции при увеличении значения переменной x, мы должны исследовать поведение функции при стремлении x к бесконечности.
Предположим, что x → \infty. Тогда, при увеличении значения переменной x, мы можем заметить, что значение функции f(x) становится все меньше и меньше, но никогда не достигает нуля.
Математически, можно записать:
\lim_{{x
ightarrow\infty}} f(x) = \lim_{{x
ightarrow\infty}} \frac{1}{x} = 0
Таким образом, мы получаем, что конечный предел функции f(x) = \frac{1}{x} при увеличении значения переменной x равен нулю.
Пример 2: Конечный предел при уменьшении значения переменной
Рассмотрим функцию f(x) = 1/x и найдем ее предел при x, стремящемся к нулю.
Составим таблицу значений функции f(x) для разных значений x:
| x | f(x) |
|---|---|
| 1 | 1 |
| 0.1 | 10 |
| 0.01 | 100 |
| 0.001 | 1000 |
| 0.0001 | 10000 |
Из таблицы видно, что при уменьшении значения x функция f(x) стремится к бесконечности. Формально это можно записать как:
limx→0 (1/x) = ∞
Таким образом, наш пример демонстрирует, что при определенных условиях конечный предел может быть равен бесконечности.








