Формулировка теоремы - это очень важный аспект математического и научного мышления. Она является своего рода "контрактом", который устанавливает основные условия и выводы, сформулированные в рамках определенной теории или концепции.
В формулировке теоремы выделяют основные элементы - условия и выводы. Условия, как правило, описывают изначальные данные или предположения, а выводы - то, что должно быть доказано или следует из этих условий. Формулировка теоремы позволяет сформулировать задачу точно и понять, какие утверждения требуется доказать.
Важность формулировки теоремы трудно переоценить. Она позволяет ученым точно определить суть и значимость своих открытий, а также обеспечивает понимание и восприятие результатов исследований другими людьми. Формулировка теоремы является неотъемлемым компонентом математических публикаций и научных работ, и ее отсутствие может привести к недопониманию или неправильному использованию результатов исследования.
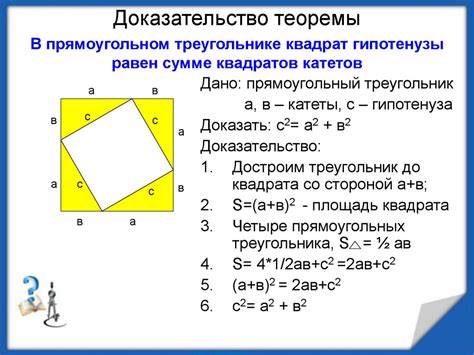
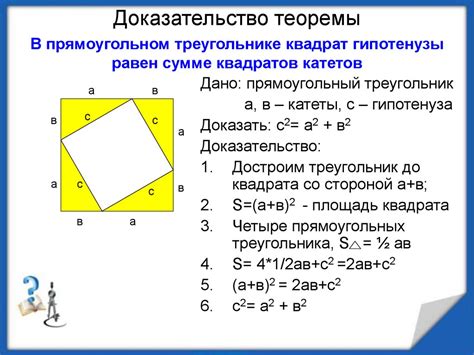
Примером формулировки теоремы может служить теорема Пифагора: "В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов". В этом случае, условием является наличие прямоугольного треугольника, а выводом является равенство суммы квадратов катетов квадрату гипотенузы. Формулировка теоремы позволяет однозначно понять, что требуется доказать и какие условия необходимы для этого.
Что такое формулировка теоремы?
Чтобы теорема была полностью и однозначно определена, ее формулировка должна включать в себя следующие элементы:
- Название теоремы: краткое наименование, отражающее суть утверждения.
- Обозначения и условия: символы и термины, используемые в формулировке, и условия, которые определяют предмет исследования.
- Утверждение: суть теоремы, точно определяющая отношение между объектами.
- Доказательство: последовательность логических шагов, которые подтверждают истинность утверждения.
- Заключение: выводы, которые следуют из утверждения и его доказательства.
Формулировка теоремы играет важную роль в математике, поскольку она позволяет установить и передать знания другим математикам и ученым. Она позволяет точно определить объекты и условия, устанавливает отношения и выводит заключения. Без формулировки теорема была бы неопределенной и не имела бы четкого смысла.
Определение и основные понятия
Формулировка теоремы часто состоит из двух частей – условия и заключения. Условие представляет собой предпосылки или предварительные утверждения, которые необходимы для доказательства заключения. Заключение формулирует основное утверждение, которое доказывается на основе предоставленных условий.
Определение теоремы должно быть ясным, точным и однозначным. Оно не должно содержать неопределённостей или двусмысленностей, чтобы избежать недопонимания и разногласий при интерпретации.
Ключевыми понятиями, связанными с формулировкой теоремы, являются:
- Условие – это часть формулировки теоремы, которая описывает предпосылки или ограничения, необходимые для доказательства заключения;
- Заключение – это часть формулировки теоремы, которая содержит основное утверждение, требующее доказательства;
- Доказательство – это процесс, который устанавливает истинность заключения на основе предоставленных условий;
- Гипотеза – это предположение, которое ещё не было доказано, но может быть доказано при выполнении определённых условий;
- Контрпример – это пример, который опровергает истинность формулировки теоремы, показывая, что она не выполняется в каком-то конкретном случае.
Роль формулировки теоремы в математике
Формулировка теоремы играет ключевую роль в математике, так как она позволяет точно и ясно выразить основные понятия, идеи и результаты, полученные в ходе исследования. Формулировка теоремы содержит в себе необходимые условия, выводы и заключения, которые делают эту теорему полезной и пригодной для дальнейшего исследования и применения в других областях математики и наук.
Прежде всего, формулировка теоремы позволяет ученым и математикам международного сообщества понять и использовать результаты и открытия друг друга. Благодаря формулировке, теоремы становятся универсальными и единообразными для всех исследователей. Математика является языком символов и формул, и формулировка теоремы является непременным условием для цивилизованного обсуждения и обмена знаниями.
Кроме того, формулировка теоремы является основой для строгого математического доказательства. Она задает четкие рамки и условия, которые должны быть выполнены для полноты и корректности доказательства. Формулировка позволяет определить, какие факты и логические шаги могут быть использованы при доказательстве, а какие – нет. Тем самым, формулировка теоремы является важным инструментом для развития и укрепления математической логики и рассуждений.
Наконец, формулировка теоремы является исходной точкой исследования. На основе формулировки, математики проводят свои эксперименты, строят модели и гипотезы, разрабатывают новые методы и техники, чтобы доказать или опровергнуть данную теорему. Формулировка теоремы определяет направление и способы ее исследования и позволяет вносить новые вклады в математическую науку.
Таким образом, формулировка теоремы является неотъемлемой частью математического исследования. Она обеспечивает ясность, точность и универсальность математических результатов, служит фундаментом для математического доказательства и исследования, а также открывает новые горизонты для развития науки.
Примеры формулировок теорем
Ниже приведены несколько примеров формулировок теорем из различных областей математики:
- Теорема Пифагора: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
- Теорема Ферма: Нет целых чисел x, y, z и n, при n > 2, таких, что x^n + y^n = z^n.
- Теорема Фундаментальной теоремы арифметики: Любое натуральное число больше 1 единственным образом представимо в виде произведения простых чисел, причем порядок простых сомножителей не имеет значения.
- Теорема Пуанкаре: Если расширенная гипотеза Римана верна, то добавление одного дополнительного условия может сделать ее доказуемой.
- Теорема Эйлера: Для любых взаимно простых натуральных чисел a и n, a^φ(n) ≡ 1 (mod n), где φ(n) - функция Эйлера, определяющая количество натуральных чисел, не превосходящих n и взаимно простых с ним.
Это лишь несколько примеров из множества теорем, которые существуют в математике. Формулировка теоремы играет важную роль, поскольку она должна ясно и точно описывать утверждение, которое будет доказываться или опровергаться.








