В математике, взаимообратные функции представляют собой пару функций, каждая из которых обращает другую. То есть, если применить одну из функций к какому-либо числу и затем применить другую функцию к результату, мы получим исходное число.
Одним из простых примеров взаимообратных функций является функция возведения в квадрат и функция извлечения корня квадратного. Если применить функцию возведения в квадрат к числу, а затем применить функцию извлечения корня к результату, мы получим исходное число.
Взаимообратные функции обладают несколькими свойствами. Одно из них - обратная функция является обратной по отношению к оригинальной функции. То есть, если f(x) обратима, то существует g(x), такая что f(g(x)) = x и g(f(x)) = x. Другое свойство - обратная функция сохраняет порядок операций. То есть, если применить f(x) к a, затем применить g(x) к результату, мы получим a. Третье свойство - обратная функция обладает такими же свойствами как и оригинальная функция, такими как периодичность и непрерывность.
В итоге, взаимообратные функции являются важным концептом в математике, который находит применение в различных областях, включая теорию чисел, алгебру, геометрию и статистику. Они позволяют обратить операцию над числами или другими объектами, исследовать свойства функций и решать уравнения. Понимание понятия взаимообратных функций помогает более глубоко понять множество математических концепций и улучшить навыки решения математических задач.
Что такое взаимообратные функции
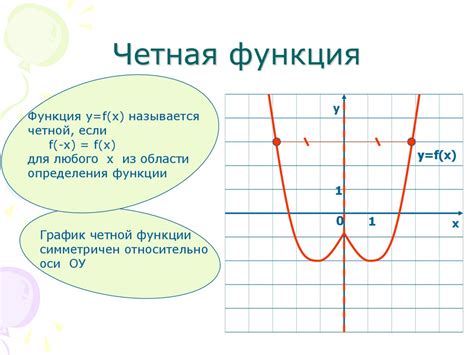
Взаимообратные функции можно воспринимать как "обратно-пропорциональные" функции, то есть если f(x) увеличивает значение x, то f^(-1)(x) уменьшает значение x и наоборот.
Однако, не все функции имеют взаимообратную функцию. Для существования взаимообратной функции, главное требование - это биективность функции. Функция является биекцией, если каждому значению в области определения соответствует единственное значение в области значений и наоборот.
Примером взаимообратных функций являются функции семейства y = x и y = x^(-1), графики которых представляют собой прямую линию и гиперболу, соответственно.
Свойства взаимообратных функций включают:
- Область определения и область значений взаимообратной функции обратны области определения и области значений исходной функции.
- Функции и их взаимообратные функции обладают свойством композиции, то есть если мы применяем функцию и затем её взаимообратную функцию (или наоборот), то получаем исходное значение.
Примеры взаимообратных функций
Ниже приведены несколько примеров взаимообратных функций:
Функции возведения в квадрат и извлечения квадратного корня:
- Функция возведения в квадрат
f(x) = x^2превращает любое число в квадрат данного числа. - Функция извлечения квадратного корня
g(x) = sqrt(x)отменяет действие функции возведения в квадрат и возвращает исходное число. - Эти две функции являются взаимообратными, так как
f(g(x)) = xиg(f(x)) = xдля любого допустимого значения x.
- Функция возведения в квадрат
Функции кодирования и декодирования:
- Функция кодирования преобразует исходное сообщение в зашифрованную форму.
- Функция декодирования отменяет действие функции кодирования и восстанавливает исходное сообщение.
- Например, шифр Цезаря - это пример взаимообратных функций кодирования и декодирования.
Функции радиуса и диаметра круга:
- Функция радиуса
f(d) = d/2превращает диаметр круга в его радиус. - Функция диаметра
g(r) = 2rотменяет действие функции радиуса и возвращает исходный диаметр. - Эти две функции являются взаимообратными, так как
g(f(d)) = dиf(g(r)) = rдля любого допустимого значения d и r.
- Функция радиуса
Это лишь несколько примеров взаимообратных функций. Взаимообратные функции широко используются в математике, программировании и других областях, где требуется отменить действие функции путем применения обратной функции.
Свойства взаимообратных функций
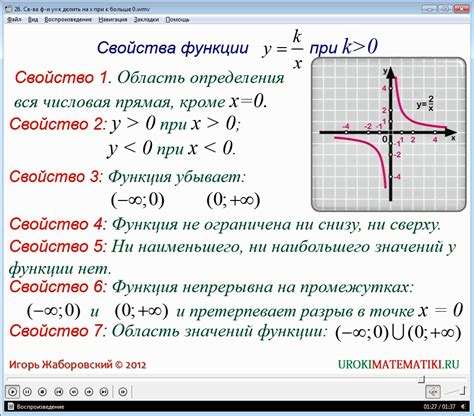
Взаимообратные функции обладают рядом важных свойств, которые позволяют использовать их при решении различных математических задач.
1. Область значений и область определения: если функции являются взаимообратными, то их область определения и область значений также будут взаимообратными. Если функция f(x) имеет область определения D, то ее обратная функция g(x) имеет область значений D и наоборот.
2. Свойство композиции: композиция взаимообратных функций d(f(x)) = x и f(d(x)) = x. Это означает, что если применить функцию f(x) к аргументу x и затем результат применить функцию g(x), то мы получим исходное значение x и наоборот.
3. Графики: графики взаимообратных функций симметричны относительно прямой y = x. Другими словами, если точка (x, y) лежит на графике функции f(x), то точка (y, x) будет лежать на графике функции g(x) и наоборот.
4. Функциональность: взаимообратные функции однозначно связаны между собой и имеют одинаковую функциональность. Это означает, что если функция f(x) обладает какими-либо свойствами (например, является монотонной или дифференцируемой), то ее обратная функция g(x) имеет те же свойства.
5. Сохранение операций: при выполнении различных операций (сложение, умножение, деление) над функциями, их взаимообратные функции также сохраняют эти операции. Например, если функции f(x) и g(x) являются взаимообратными, то (f(x) + g(x)) = x и (f(x) * g(x)) = x.
| Свойство | Описание |
|---|---|
| Область значений и область определения | Обратная функция имеет область значений и область определения, которая является взаимообратной по отношению к исходной функции. |
| Свойство композиции | Композиция взаимообратных функций позволяет получить исходные значения при последовательном применении функций. |
| Графики | Графики взаимообратных функций симметричны относительно прямой y = x. |
| Функциональность | Взаимообратные функции имеют одинаковую функциональность и связаны между собой. |
| Сохранение операций | Взаимообратные функции сохраняют операции, такие как сложение, умножение и деление. |








