Вычисление приближенных значений является одной из основных задач в математике и науке. Методы численного анализа позволяют нам получать приближенные значения функций, интегралов и других математических величин, используя численные алгоритмы и вычислительные методы.
Одним из основных методов вычисления приближенных значений является метод интерполяции. Интерполяция позволяет нам находить значения функции между заданными точками, основываясь на значениях функции в этих точках. Мы можем использовать различные формулы интерполяции, такие как линейная интерполяция, кубическая интерполяция и сплайн-интерполяция, чтобы получить более точные приближенные значения.
Другим важным методом вычисления приближенных значений является численное дифференцирование и интегрирование. Мы можем использовать численные формулы для приближенного вычисления производных и интегралов функций. Примерами таких формул являются формулы прямоугольников, трапеций и Симпсона.
Например, чтобы приближенно вычислить интеграл функции f(x) на отрезке [a, b], мы можем использовать формулу трапеций. В этом случае интеграл будет приближенно равен сумме площадей трапеций, образованных отрезками длиной h и значениями функции f(x) в точках xi. Формула для вычисления интеграла будет выглядеть следующим образом:
∫f(x)dx ≈ h * (f(a)/2 + f(x1) + f(x2) + ... + f(b)/2)
Таким образом, методы численного анализа позволяют нам находить приближенные значения различных математических величин с заданной точностью. Они широко применяются в различных областях науки и техники, таких как физика, экономика, компьютерные науки и другие.
Приближенное значение: что это такое?
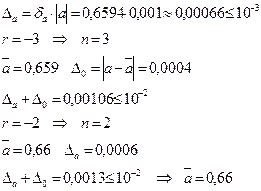
Методы приближенного вычисления используются в различных областях, где точное значение может быть сложно или дорого получить. Например, в физике, математике, инженерии и экономике. Они позволяют получить быстрый и приемлемый результат, не требуя сложных и ресурсоемких вычислений.
Одним из наиболее известных методов приближенного вычисления является метод конечных разностей, который используется для вычисления производных и решения дифференциальных уравнений. Он основан на аппроксимации функции с помощью разностного равенства и шага, который определяет точность приближения.
Другим примером метода приближенного вычисления является метод Ньютона, который используется для нахождения корней уравнений. Он основан на итерационном процессе, который позволяет приблизиться к корню с каждой итерацией.
Важно понимать, что приближенное значение не является точным и может содержать погрешности. Однако, оно может быть достаточно точным для решения практических задач или получения общего представления о поведении функции или системы.
Зачем нужно вычислять приближенное значение?
Одной из основных причин, по которым мы вычисляем приближенные значения, является отсутствие точных или аналитических решений для сложных задач. Нередко мы сталкиваемся с функциями или системами уравнений, для которых нет известного аналитического решения. В таких случаях приближенные методы позволяют нам получить приближенное значение решения, которое близко к истинному.
Вычисление приближенных значений также позволяет нам проводить численное моделирование и анализ. Мы можем использовать приближенные значения для аппроксимации сложных функций и систем, проводить исследования и анализировать их поведение. Это особенно важно, когда точные значения неизвестны или недоступны.
Приближенные значения играют важную роль в финансовой математике и статистике. Например, при оценке стоимости финансовых инструментов или при проведении экономического анализа, мы часто используем приближенные методы для моделирования и прогнозирования поведения рынка.
Таким образом, вычисление приближенных значений является неотъемлемой частью научного и инженерного подхода. Оно позволяет нам получать оценки и аппроксимации, которые помогают нам моделировать и анализировать сложные системы и функции, приближаться к истинным значениям и принимать важные решения на основе этих оценок.
Методы вычисления приближенного значения

Вычисление приближенного значения играет важную роль во многих областях науки и техники. Существуют различные методы, позволяющие получить приближенное значение для разных математических функций или уравнений.
Одним из наиболее распространенных методов является метод Ньютона. Он основан на итерационном процессе, при котором последовательно уточняется приближенное значение функции до достижения заданной точности. Метод Ньютона широко применяется при решении уравнений и систем уравнений.
Еще одним методом вычисления приближенного значения является метод бисекции. Он основан на принципе деления отрезка пополам, при котором последовательно выбираются новые отрезки, содержащие корень функции. Метод бисекции применяется в основном для вычисления корней одномерных функций.
Метод наименьших квадратов также может быть использован для получения приближенного значения. Он позволяет аппроксимировать заданные данные при помощи линейной или нелинейной функции, минимизируя сумму квадратов отклонений точек данных от этой функции.
Кроме того, существуют дробно-линейные и интерполяционные методы, которые также позволяют получить приближенное значение функции на основе известных данных.
- Метод Ньютона
- Метод бисекции
- Метод наименьших квадратов
- Дробно-линейные методы
- Интерполяционные методы
Выбор конкретного метода зависит от природы задачи и требуемой точности. Важно выбрать метод, который наилучшим образом соответствует поставленной задаче и позволяет получить приемлемый результат.
Метод интерполяции
Основная идея метода интерполяции заключается в следующем. Пусть имеются некоторые известные точки на графике функции. Интерполяция позволяет найти значения функции в промежуточных точках между известными точками.
Существует несколько способов интерполяции, таких как линейная интерполяция, полиномиальная интерполяция или сплайн-интерполяция. Каждый из этих методов имеет свои преимущества и ограничения, и выбор метода зависит от конкретной задачи и требуемой точности результата.
При использовании метода интерполяции необходимо учитывать, что точность аппроксимации будет зависеть от количества известных точек и выбора конкретного метода. Чем больше точек используется для интерполяции и чем более сложный метод выбран, тем точнее будет результат, но и тем больше вычислительных затрат потребуется.
Метод интерполяции широко применяется в различных областях, таких как математика, физика, экономика и технические науки. Он позволяет аппроксимировать сложные функции, получать значения функций в неизвестных точках и решать задачи, связанные с оптимизацией и моделированием.
В итоге, метод интерполяции является мощным инструментом для вычисления приближенных значений функций и нахождения решений в широком спектре задач.
Метод экстраполяции
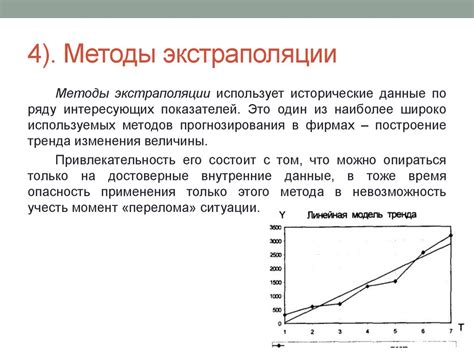
Метод экстраполяции, также известный как метод продолжения ряда или метод продолжения функции, используется для вычисления приближенного значения функции или ряда вне заданного диапазона значений, основываясь на известных значениях функции или ряда внутри этого диапазона.
Этот метод основывается на предположении о подобности поведения функции или ряда внутри и вне заданного диапазона. С помощью метода экстраполяции можно продолжить функцию или ряд за пределы известного диапазона, что позволяет получить приближенное значение функции или ряда вне этого диапазона.
Для применения метода экстраполяции необходимо иметь достаточное количество известных значений функции или ряда внутри заданного диапазона. Затем на основе этих значений можно построить уравнение или выразить функцию в виде ряда, которые можно использовать для вычисления приближенного значения вне диапазона.
Одним из примеров применения метода экстраполяции является вычисление значения функции вне заданного диапазона по условиям краевых задач. В этом случае известны значения функции на границе заданного диапазона, и используя метод экстраполяции, можно получить приближенное значение функции внутри заданного диапазона.
Метод численного интегрирования
Существует несколько методов численного интегрирования, каждый из которых имеет свои особенности и применяется в различных ситуациях:
- Метод прямоугольников: основан на аппроксимации функции постоянным значением на каждом интервале интегрирования.
- Метод трапеций: основан на аппроксимации функции линейной функцией на каждом интервале.
- Метод Симпсона: основан на аппроксимации функции параболой на каждом интервале.
- Другие методы, такие как метод Гаусса и метод Монте-Карло.
Для использования метода численного интегрирования необходимо задать функцию, пределы интегрирования и требуемую точность. Чем меньше интервалы разбиения и высокая точность вычислений, тем более точный результат будет получен.
Метод численного интегрирования широко применяется в различных областях, включая математику, физику, экономику и инженерию. Он позволяет вычислять значения сложных интегралов, для которых нет аналитического решения.
Методы приближенного решения уравнений

Одним из наиболее распространенных методов приближенного решения уравнений является метод половинного деления или метод бисекции. Суть метода заключается в поиске корня уравнения на заданном интервале, который делится пополам на каждой итерации. Если значения функции на концах интервала противоположны по знаку, то корень уравнения находится внутри интервала. Затем интервал с половинным делением сужается до тех пор, пока не будет достигнута требуемая точность или заданное число итераций.
Еще одним распространенным методом является метод Ньютона. Он основан на итерационной формуле, которая использует производную функции для приближенного нахождения корня. На каждой итерации формула обновляется, пока не будет достигнута требуемая точность. Метод Ньютона обеспечивает быструю сходимость и может быть использован для решения широкого спектра уравнений, однако в некоторых случаях может потребоваться начальное приближение, близкое к корню уравнения.
Кроме того, существуют и другие методы приближенного решения уравнений, такие как метод секущих, метод хорд и метод простой итерации. Каждый из этих методов имеет свои особенности и применим в разных случаях.
Важно отметить, что при приближенном решении уравнений необходимо учитывать возможные ошибки и ограничения выбранного метода. Также стоит помнить о возможности множественных корней уравнения и необходимости правильного выбора начального приближения для методов итерационного типа.
Пример вычисления приближенного значения с использованием метода интерполяции
Рассмотрим пример: у нас есть набор данных, представленных в виде таблицы, где в первом столбце указаны значения аргумента x, а во втором столбце - соответствующие значения функции y:
| x | y |
|---|---|
| 1 | 2 |
| 3 | 4 |
| 5 | 6 |
Нам необходимо найти значение функции y при значении аргумента x=2. Для этого мы можем воспользоваться методом интерполяции.
Применим линейную интерполяцию - это простой метод, который предполагает, что наша функция является линейной на интервале между двумя ближайшими известными точками.
Значение функции на интервале между точками x=1 и x=3 может быть вычислено по формуле:
y = y1 + (x - x1) * (y2 - y1) / (x2 - x1)
В нашем случае, x1=1, x2=3, y1=2, y2=4, и x=2. Подставим эти значения в формулу:
y = 2 + (2 - 1) * (4 - 2) / (3 - 1) = 2 + 1 * 2 / 2 = 2 + 2 / 2 = 2 + 1 = 3
Таким образом, приближенное значение функции y при x=2 равно 3.
Пример вычисления приближенного значения с использованием метода экстраполяции
Метод экстраполяции позволяет найти приближенное значение функции за пределами имеющихся данных. Рассмотрим пример вычисления приближенного значения с использованием данного метода.
Предположим, что имеются некоторые измерения зависимости некоторой величины y от другой величины x. Допустим, у нас есть следующие значения:
| x | y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
Предположим также, что мы хотим найти значение функции y при x=5. Для этого мы можем использовать метод экстраполяции.
Один из методов экстраполяции - это метод линейной экстраполяции, который предполагает, что зависимость между x и y является линейной. Для этого мы можем построить линию, проходящую через две последние точки (x=3, y=6 и x=4, y=8) и использовать ее для вычисления значения y при x=5.
Для построения линии проходящей через эти две точки, мы можем воспользоваться формулой уравнения прямой:
y = mx + b
где m - угловой коэффициент прямой, а b - свободный член прямой.
Для нашего примера, угловой коэффициент можно найти следующим образом:
m = (y2 - y1) / (x2 - x1)
где (x1, y1) - первая точка, а (x2, y2) - вторая точка.
В нашем примере, x1=3, y1=6, x2=4, y2=8:
m = (8 - 6) / (4 - 3) = 2
Теперь, чтобы найти свободный член b, мы можем использовать одно из известных уравнений прямой и известные значения y и x:
y = mx + b
6 = 2 * 3 + b
Решая это уравнение для b, получаем:
b = 6 - 2 * 3 = 0
Таким образом, уравнение прямой, проходящей через две последние точки будет выглядеть следующим образом:
y = 2x + 0
Теперь мы можем использовать это уравнение для вычисления значения y при x=5:
y = 2 * 5 + 0 = 10
Таким образом, приближенное значение функции y при x=5 будет равно 10.
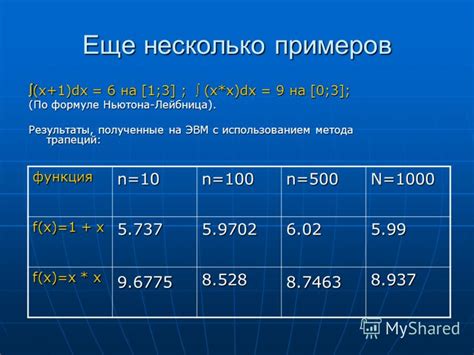
Пример вычисления приближенного значения с использованием метода численного интегрирования
Метод прямоугольников основан на аппроксимации подынтегральной функции прямоугольниками. Для вычисления приближенного значения интеграла необходимо разбить отрезок интегрирования на равные отрезки и вычислить сумму площадей прямоугольников, образованных подынтегральной функцией.
Допустим, необходимо вычислить приближенное значение интеграла функции f(x) на отрезке [a, b]. Для этого сначала выбирается число разбиений n. Затем, отрезок интегрирования разбивается на n равных отрезков шириной h, где h = (b - a) / n.
Найдем приближенное значение интеграла функции f(x) на отрезке [a, b] с помощью метода прямоугольников.
function rectangleMethod(f, a, b, n) {
var h = (b - a) / n;
var sum = 0;
for (var i = 0; i
В данном примере используется анонимная функция для определения подынтегральной функции f(x), а также для задания отрезка интегрирования [a, b] (в данном случае, от 0 до 1). Параметр n задает число разбиений отрезка интегрирования. Чем больше значение n, тем точнее будет приближенное значение интеграла.








