Расходящийся интеграл - это интеграл, который не приобретает конечных значений при его вычислении. В отличие от сходящегося интеграла, расходящийся интеграл не имеет определенного значения и его значение может быть неограниченным.
Он возникает при интегрировании функций, которые не удовлетворяют условию сходимости - условию, при котором интеграл существует и имеет конечное значение. Такие функции обычно имеют особенности или имеют неограниченное поведение в точках интегрирования.
Примером функции с расходящимся интегралом является функция f(x) = 1/x. Интеграл от этой функции в пределах от 1 до бесконечности не сходится к конечному значению. Он растет неограниченно, поскольку функция 1/x стремится к бесконечности при x, стремящемся к нулю.
Особенно важно понимать, что расходящийся интеграл не означает, что функция неинтегрируема. Функция может быть интегрируемой, но иметь неограниченный интеграл.
Расходящийся интеграл имеет ряд важных применений в математике и естественных науках, особенно в физике. Например, расходящиеся интегралы могут возникать при расчете сумм энергии в физических системах или при интегрировании распределений вероятностей.
В заключение, расходящийся интеграл - это интеграл, значение которого не ограничено и он не приобретает конечных значений при вычислении. Они возникают при интегрировании функций, которые не удовлетворяют условию сходимости и могут иметь особенности или неограниченное поведение. Важно отличать расходящиеся интегралы от неинтегрируемых функций, так как функции могут быть интегрируемыми, но иметь неограниченный интеграл.
Что такое расходящийся интеграл?

Если интеграл является расходящим, то это означает, что функция не ограничена на данном промежутке и имеет бесконечно много точек, где она неопределена или неограничена.
Расходящиеся интегралы могут возникать при интегрировании функций, которые имеют особенности, такие как вертикальные асимптоты, полюса, разрывы и т.д.
Знание того, что интеграл расходится, имеет важное значение при решении задач математического анализа и при вычислении площадей под кривыми. Оно позволяет определить, что данная функция не является интегрируемой на рассматриваемом промежутке, и может потребовать использования альтернативных подходов для нахождения площади или вычисления интеграла.
Определение расходящегося интеграла
В математике расходящимся интегралом называется интеграл, значение которого стремится к бесконечности или не существует. Это означает, что при интегрировании функции на определенном интервале результат будет бесконечным или неопределенным.
Формально, интеграл функции \(f(x)\) на интервале \([a, b]\) считается расходящимся, если его значение равно плюс или минус бесконечности или не существует. Расходящийся интеграл обозначается символом \(\infty\) или \(-\infty\).
Если при интегрировании функции результат получается бесконечным, это может быть связано с тем, что функция имеет устремление к бесконечности на данном интервале, имеет вертикальную асимптоту или неограниченный рост. В таких случаях интеграл не имеет конечного значения и считается расходящимся.
Например, рассмотрим функцию \(f(x) = \frac{1}{x}\) на интервале \([1, +\infty)\). При интегрировании этой функции на указанном интервале, значение интеграла будет стремиться к плюс бесконечности. Таким образом, интеграл \(\int_{1}^{+\infty} \frac{1}{x} dx\) будет расходящимся.
Расходящиеся интегралы имеют важное значение в математическом анализе и используются, например, для определения площади неограниченных фигур или областей под кривыми, которые стремятся к бесконечности или имеют бесконечную площадь.
Причины появления расходящегося интеграла

Расходящийся интеграл возникает, когда значение определенного интеграла не сходится к конечному числу, а стремится к бесконечности или не определено вообще.
Существует несколько причин, по которым интеграл может считаться расходящимся:
1. Неограниченность функции в пределах интегрирования
Если функция, интеграл которой вычисляется, имеет бесконечное значение в пределах интегрирования, то интеграл будет расходящимся. Например, рассмотрим интеграл ∫(1/x)dx от 1 до бесконечности. Функция 1/x не определена в точке x=0, и ее значение стремится к бесконечности при x, стремящемся к нулю. Поэтому этот интеграл считается расходящимся.
2. Отсутствие предела интегрирования
Если предел интегрирования в определенном интеграле не существует или равен бесконечности, то интеграл будет расходящимся. Например, рассмотрим интеграл ∫(1/x)dx от 0 до 1. Функция 1/x не определена в точке x=0, и этот предел считается несуществующим. Поэтому этот интеграл также считается расходящимся.
3. Отрицательность интеграла
Если значение интеграла от функции всегда отрицательно или бесконечно отрицательно в пределах интегрирования, то интеграл считается расходящимся. Например, рассмотрим интеграл ∫(-x)dx от 0 до бесконечности. Функция -x всегда имеет отрицательное значение, поэтому этот интеграл считается расходящимся.
Изучение и анализ причин появления расходящегося интеграла является важным для понимания свойств и использования интегралов в математике и научных исследованиях.
Примеры расходящихся интегралов
Ниже приведены несколько примеров расходящихся интегралов:
Интеграл от функции 1/x
Интеграл от функции f(x) = 1/x можно записать следующим образом:
∫(1/x)dx
Если брать интеграл от этой функции на интервале от 1 до бесконечности, то значение интеграла будет расходиться и стремиться к бесконечности.
Интеграл от функции e^x
Интеграл от функции f(x) = e^x можно записать следующим образом:
∫(e^x)dx
Если брать интеграл от этой функции на интервале от 0 до бесконечности, то значение интеграла также будет расходиться и стремиться к бесконечности.
Интеграл от функции 1/x^2
Интеграл от функции f(x) = 1/x^2 можно записать следующим образом:
∫(1/x^2)dx
Если брать интеграл от этой функции на интервале от 1 до бесконечности, то значение интеграла будет также расходиться и стремиться к бесконечности.
Все эти примеры демонстрируют, что интегралы могут иметь расходящиеся значения, что требует особого внимания и осторожности при работе с ними.
Пример 1

Рассмотрим интеграл, который расходится:
$$\int_{0}^{+\infty} \frac{\sin{x}}{x} dx.$$
Пусть $I$ - значение данного интеграла.
Воспользуемся тем, что для любого значения $x$ выполняется неравенство:
$$-1 \leq \sin{x} \leq 1.$$
Таким образом, получаем:
$$-\int_{0}^{+\infty} \frac{1}{x} dx \leq \int_{0}^{+\infty} \frac{\sin{x}}{x} dx \leq \int_{0}^{+\infty} \frac{1}{x} dx.$$
0 будет являться нижней границей такого интеграла, а $+\infty$ - верхней.
Так как интеграл от функции $\frac{1}{x}$ расходится при $x
ightarrow 0$ и $x
ightarrow +\infty$, то, в соответствии с сравнительным критерием сходимости интеграла, исследуемый интеграл также расходится.
Пример 2
Рассмотрим следующий интеграл:
∫ (1/x) dx
Интеграл данной функции не является сходящимся. Посмотрим на ее график:
(здесь должен быть изображен график функции)
Мы видим, что функция 1/x имеет вертикальную асимптоту при x=0. Это означает, что функция стремится к положительной или отрицательной бесконечности при x, стремящемся к 0. Таким образом, интеграл от функции 1/x расходится.
Пример 3
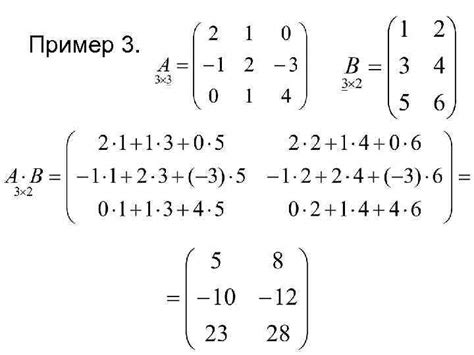
Рассмотрим следующий интеграл:
$$\int_{0}^{\infty} \frac{1}{x^3+x} dx.$$
Перед тем как переходить к вычислению интеграла, нужно убедиться, что функция под интегралом является непрерывной и ограниченной на рассматриваемом отрезке. В данном случае функция $f(x) = \frac{1}{x^3+x}$ непрерывна и ограничена на отрезке $[0, \infty)$, поэтому можем приступить к вычислению.
Используя метод частных дробей, преобразуем подынтегральную функцию:
$$\frac{1}{x^3+x} = \frac{1}{x(x^2+1)} = \frac{A}{x} + \frac{Bx+C}{x^2+1},$$
где $A$, $B$ и $C$ - некоторые неизвестные числа. Найдем их значения, умножив обе части на знаменатель:
$$1 = A(x^2+1) + (Bx+C)x.$$
Раскроем скобки и соберем подобные слагаемые:
$$1 = (A+B)x^2 + Cx + A.$$
Получаем систему уравнений:
\[\begin{cases} A+B = 0 \\ C = 0 \\ A = 1 \end{cases}\]
Из первого уравнения получаем $A = 1$ и $B = -A = -1$. Подставляя эти значения во второе уравнение, получаем $C = 0$. Таким образом, имеем:
$$\frac{1}{x^3+x} = \frac{1}{x} - \frac{x}{x^2+1}.$$
Перейдем к вычислению интеграла:
\(\begin{align*}
\int_{0}^{\infty} \frac{1}{x^3+x} dx &= \int_{0}^{\infty} \left(\frac{1}{x} - \frac{x}{x^2+1}
ight) dx \\
&= \lim_{{a\to\infty}} \int_{0}^{a} \frac{1}{x} dx - \lim_{{a\to\infty}} \int_{0}^{a} \frac{x}{x^2+1} dx.
\end{align*}\)
Вычислим первый интеграл:
\(\begin{align*}
\lim_{{a\to\infty}} \int_{0}^{a} \frac{1}{x} dx &= \lim_{{a\to\infty}} \left[\ln|x|
ight]_{0}^{a} \\
&= \lim_{{a\to\infty}} \ln|a| - \lim_{{a\to\infty}} \ln|0| \\
&= \lim_{{a\to\infty}} \ln|a| - \lim_{{a\to\infty}} (-\infty) \\
&= \infty.
\end{align*}\)
Второй интеграл можно вычислить с помощью замены \(u = x^2+1\). Тогда \(du = 2x \, dx\) и \(\frac{1}{2}du = x \, dx\), и, соответственно:
\(\begin{align*}
\lim_{{a\to\infty}} \int_{0}^{a} \frac{x}{x^2+1} dx &= \lim_{{a\to\infty}} \int_{1}^{a^2+1} \frac{1}{2} \frac{1}{u} du \\
&= \lim_{{a\to\infty}} \left[\frac{1}{2}\ln|u|
ight]_{1}^{a^2+1} \\
&= \lim_{{a\to\infty}} \frac{1}{2}\ln|a^2+1| - \lim_{{a\to\infty}} \frac{1}{2}\ln|1| \\
&= \frac{1}{2}\ln|a^2+1| - 0 \\
&= \infty.
\end{align*}\)
Итак, получаем:
\(\begin{align*}
\int_{0}^{\infty} \frac{1}{x^3+x} dx &= \infty - \infty \\
&= \text{расходится}.
\end{align*}\)
Таким образом, представленный интеграл расходится.
Последствия использования расходящихся интегралов
Использование расходящихся интегралов может иметь несколько значимых последствий, особенно в контексте математических вычислений и применений.
1. Несуществование предела: Если интеграл расходится, это означает, что предел интегрируемой функции не существует на заданном интервале. Это может оказаться проблематичным при решении задач, требующих определения точных значений или нахождения пределов функций.
2. Некорректные результаты: Использование расходящихся интегралов может привести к получению некорректных результатов в вычислениях или при решении задач. Такие результаты могут быть непредсказуемыми и не соответствовать реальности.
3. Ограниченная применимость: Расходящиеся интегралы имеют ограниченную применимость в контексте математического анализа и других областей, где требуется точное и надежное решение. В большинстве случаев расходящиеся интегралы применяются для исследования поведения функций и для построения асимптотических моделей.
4. Теоретическое исследование: Расходящиеся интегралы также могут иметь важное значение в теоретическом исследовании. Изучение и анализ таких интегралов помогает развивать новые математические концепции и методы. Они могут служить основой для создания новых теорий и техник в математике и других научных дисциплинах.
В целом, использование расходящихся интегралов требует осторожности и дополнительного анализа. Они могут помочь в понимании особенностей функций и их поведения, но могут также привести к ошибочным результатам и недостоверным выводам, если их применение осуществляется без достаточного понимания и контроля.
Потеря точности вычислений

При выполнении численных вычислений, особенно в случае с расходящимся интегралом, возможна потеря точности. Это связано с ограниченной точностью представления чисел в компьютерах.
Компьютеры представляют числа в виде двоичных дробей с ограниченной точностью. Обычно используется стандарт IEEE 754, который предусматривает хранение чисел с плавающей точкой в формате одинарной или двойной точности. Одинарная точность представляет число с плавающей точкой в виде 32 бит, а двойная точность - в виде 64 бит.
Однако, при выполнении сложных вычислений, таких как вычисление интегралов, возникают округления и ошибки приближения, которые могут накапливаться и приводить к значительной потере точности результата.
Один из способов справиться с потерей точности - использование библиотек специального программного обеспечения, которые позволяют работать с числами с большей точностью. Такие библиотеки, как mpfr или mpc, предоставляют возможность работать с числами произвольной точности и позволяют увеличить точность вычислений.
Еще одним способом снижения потери точности является использование алгоритмов численного интегрирования с адаптивной точностью. Такие алгоритмы позволяют увеличивать или уменьшать количество точек, в которых вычисляется значение функции, в зависимости от требуемой точности.
| Пример | Увеличение точности |
|---|---|
integrate(f, a, b, n) | Увеличение количества точек разбиения на интервале [a, b] |
adaptiveIntegrate(f, a, b, eps) | Автоматическое увеличение или уменьшение количества точек в зависимости от требуемой точности |
Недостоверность результатов
Важно отметить, что расходящийся интеграл может привести к недостоверным результатам. При вычислении расходящегося интеграла необходимо быть внимательным и осторожным, так как его значение не может быть точно определено.
При расчете расходящегося интеграла может возникнуть несколько проблем. Во-первых, интеграл может не иметь окончательного значения, так как его верхний или нижний предел может быть бесконечным. Это может быть вызвано, например, наличием особенностей в функции, которые приводят к бесконечному росту или убыванию.
Во-вторых, при расчете расходящегося интеграла могут возникать проблемы с расходимостью ряда или последовательности, которая стоит в основе определения интеграла. В таких случаях интеграл может иметь значение, которое не является действительным числом, а скорее является равным плюс или минус бесконечности.
Таким образом, результаты расчетов расходящихся интегралов могут быть недостоверными и непригодными для использования в практических целях. Необходимо учитывать этот факт при работе с расходящимися интегралами и быть осторожными в интерпретации их значений.








