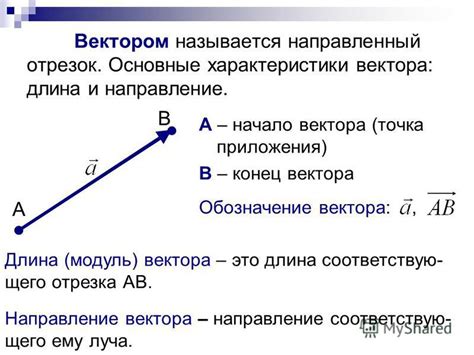
В линейной алгебре пронормированный вектор — это вектор, длина которого равна 1. Такой вектор часто используется в различных приложениях, таких как машинное обучение, компьютерная графика и физика. Получение пронормированного вектора имеет несколько способов, один из которых называется нормализацией.
Нормализация вектора — это процесс приведения его длины к значению 1 путем деления каждой компоненты вектора на его длину. Отношение между длиной вектора и его компонентами можно представить следующим образом: длина вектора равна квадратному корню из суммы квадратов его компонентов. После нормализации все компоненты вектора будут относиться к промежутку от -1 до 1.
Пример: Допустим, у нас есть вектор V с компонентами (2, 4, 6). Его длина равна √(2^2 + 4^2 + 6^2) = √(4 + 16 + 36) = √56. Чтобы получить пронормированный вектор, мы должны разделить каждую компоненту на длину вектора: (2/√56, 4/√56, 6/√56). Таким образом, пронормированный вектор будет иметь компоненты, равные примерно (0.22, 0.44, 0.67).
Пронормированные векторы полезны при работе с большими и разнородными данными, так как они позволяют сравнивать векторы с помощью углов и косинусных расстояний, а не абсолютных значений исходных компонент. Они также облегчают вычисления векторных операций, таких как скалярное произведение и векторное произведение.
Характеристики пронормированного вектора
| Характеристика | Описание |
|---|---|
| Длина | Длина пронормированного вектора всегда равна 1. |
| Направление | Пронормированный вектор указывает в том же направлении, что и исходный вектор. |
| Значение | Значение пронормированного вектора не зависит от длины исходного вектора, только от его направления. |
Пронормированные векторы широко используются в различных областях, включая линейную алгебру, компьютерную графику, машинное обучение и другие. Они помогают упростить вычисления и придать определенные свойства векторным данным. Например, в машинном обучении пронормированные векторы могут использоваться для улучшения точности моделей и предотвращения проблем с вычислениями.
Определение пронормированного вектора
Для получения пронормированного вектора необходимо разделить каждую компоненту исходного вектора на его длину. Длина вектора может быть найдена с помощью формулы Евклидовой нормы. После нормирования вектора, его длина будет равна 1.
Пример:
Пусть у нас есть вектор A = (2, 3). Чтобы получить пронормированный вектор, мы сначала найдем его длину:
|A| = √(2^2 + 3^2) = √(4 + 9) = √13.
Затем разделим каждую компоненту вектора A на длину, чтобы получить пронормированный вектор:
Aнорм = (2/√13, 3/√13).
Теперь вектор Aнорм является пронормированным вектором с длиной, равной 1.
Как получить пронормированный вектор
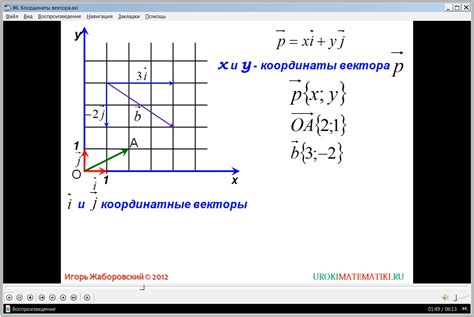
Для начала, вычислим длину вектора с помощью формулы:
длина вектора = √(x2 + y2 + z2 + ...)
где x, y, z и т.д. - координаты вектора.
Затем, каждый элемент вектора необходимо разделить на длину вектора, чтобы получить пронормированный вектор. Формула для получения пронормированного вектора будет выглядеть следующим образом:
пронормированный вектор = (x / длина вектора, y / длина вектора, z / длина вектора, ...)
Приведем пример: у нас есть вектор (3, 4). Чтобы получить его пронормированную форму, необходимо следовать описанному выше алгоритму:
Длина вектора:
длина = √(32 + 42) = √(9 + 16) = √25 = 5
Пронормированный вектор:
пронормированный вектор = (3 / 5, 4 / 5) = (0.6, 0.8)
Таким образом, пронормированный вектор для вектора (3, 4) будет иметь значения (0.6, 0.8).
Примеры пронормированных векторов
Ниже представлены примеры пронормированных векторов:
Пример 1:
Вектор v = (2, 3, 4).
Длина вектора v = √(2^2 + 3^2 + 4^2) = √(4 + 9 + 16) = √29.
Пронормированный вектор v = (2/√29, 3/√29, 4/√29).
Пример 2:
Вектор w = (-3, 0, 1).
Длина вектора w = √((-3)^2 + 0^2 + 1^2) = √(9 + 0 + 1) = √10.
Пронормированный вектор w = (-3/√10, 0/√10, 1/√10).
Пример 3:
Вектор u = (1, 1, 1, 1).
Длина вектора u = √(1^2 + 1^2 + 1^2 + 1^2) = √4 = 2.
Пронормированный вектор u = (1/2, 1/2, 1/2, 1/2).
Преимущества использования пронормированного вектора

Использование пронормированных векторов приносит следующие преимущества:
| 1. | Удобство сравнения: пронормированные векторы легко сравнивать между собой, основываясь на угле или косинусе угла между ними. Это позволяет эффективно находить ближайшие соседей или определять сходство между объектами. |
| 2. | Устойчивость к изменению масштаба: пронормированные векторы остаются неизменными при изменении их длины или масштаба, что позволяет эффективно работать с данными разного масштаба без потери информации. |
| 3. | Вычислительная эффективность: преобразование и нормирование векторов требует минимальных вычислительных затрат и может быть выполнено быстро для большого объема данных. |
| 4. | Интерпретация: пронормированные векторы имеют удобную интерпретацию, отражающую их направление и взаимосвязь с другими векторами. |
Таким образом, использование пронормированных векторов позволяет эффективно решать задачи сравнения, классификации и анализа данных, и обеспечивает более надежные и интерпретируемые результаты.
Значение пронормированного вектора в математике
Для получения пронормированного вектора необходимо разделить каждую компоненту вектора на его длину. Длина вектора вычисляется с использованием формулы Евклида: длина вектора равна корню квадратному из суммы квадратов его компонент. После вычисления длины вектора каждая компонента делится на эту длину. Полученный результат является пронормированным вектором.
Например, у нас есть вектор V = (2, 4, 6). Для того чтобы получить пронормированный вектор, сначала вычислим его длину:
| V | Длина |
|---|---|
| (2, 4, 6) | √(2^2 + 4^2 + 6^2) = √(4 + 16 + 36) = √56 ≈ 7.48 |
Затем каждая компонента делится на длину:
| V | Пронормированный вектор |
|---|---|
| (2, 4, 6) | (2/7.48, 4/7.48, 6/7.48) ≈ (0.27, 0.54, 0.81) |
Таким образом, пронормированный вектор для вектора V равен (0.27, 0.54, 0.81).
Пронормированные векторы часто используются для нормализации данных или для работы с векторами единичной длины. Они позволяют стандартизировать векторы, что делает их более удобными для анализа и сравнения. Пронормированные векторы также используются в алгоритмах машинного обучения, например, в нейронных сетях или методах классификации данных.
Роль пронормированного вектора в машинном обучении
Одно из преимуществ использования пронормированных векторов состоит в том, что они позволяют избежать проблемы масштабирования при сравнении векторов. При работе с пронормированными векторами, все компоненты вектора имеют одинаковый диапазон значений и вносят равный вклад в итоговую меру сходства или расстояния.
Пронормированные векторы часто используются в алгоритмах классификации, кластеризации и рекомендательных системах. Например, в алгоритме ближайших соседей (k-Nearest Neighbors, k-NN) для определения сходства между объектами используются расстояния между их пронормированными векторами. В рекомендательных системах пронормированные векторы могут использоваться для определения близости вкусов или предпочтений пользователей.
Для получения пронормированного вектора необходимо разделить каждую компоненту исходного вектора на его длину, то есть норму. Норму вектора можно вычислить с помощью различных метрик, таких как евклидова или манхэттенская. Затем каждая компонента вектора делится на норму, и в результате получается пронормированный вектор.
Пронормированный вектор помогает создавать более стабильные и точные модели машинного обучения. Использование пронормированных векторов может улучшить качество классификации и кластеризации, а также повысить эффективность рекомендательных систем, что делает их незаменимым инструментом в машинном обучении.
Выводы о пронормированном векторе
Пронормированный вектор представляет собой вектор, который имеет длину равную 1. Это достигается путем деления исходного вектора на его евклидову норму.
Пронормированный вектор представляет собой единичный вектор, который указывает в направлении исходного вектора, но имеет единичную длину. Он полезен для многих задач анализа данных и машинного обучения, таких как кластеризация и классификация.
Процесс нормализации вектора может помочь сделать данные более сопоставимыми и устойчивыми к различным изменениям масштаба. Он также может упростить вычисления и улучшить процесс обучения моделей.
Пример использования пронормированного вектора может быть следующим:
- Вычислить исходный вектор.
- Найти евклидову норму исходного вектора.
- Разделить исходный вектор на его евклидову норму.
- Получить пронормированный вектор, который будет указывать в том же направлении, но иметь длину равную 1.
В результате мы получаем пронормированный вектор, который будет полезен во многих задачах анализа данных и машинного обучения.








