Приведенная матрица является одной из основных концепций в линейной алгебре. Она представляет собой матрицу, в которой все элементы, кроме угловых, равны нулю. Такая матрица обладает рядом важных свойств и часто используется при решении задач в различных областях науки и техники.
В линейной алгебре приведенные матрицы используются для наглядного представления систем линейных уравнений и выражения их в матричной форме. Используя приведенные матрицы, можно упростить вычисления и решение систем уравнений, а также изучать различные свойства матричных операций.
Приведение матрицы - это процесс приведения всех элементов матрицы, кроме угловых, к нулю. Для этого применяются элементарные преобразования, такие как умножение строки матрицы на ненулевое число или сложение строк матрицы. В результате приведения матрицы к приведенному виду, мы получаем приведенную матрицу, в которой все элементы, кроме угловых, равны нулю.
Приведенная матрица играет важную роль в решении систем линейных уравнений и применяется во многих областях, таких как физика, экономика, инженерия и компьютерная графика. Понимание ее значения и использование в линейной алгебре поможет эффективно решать задачи и упростить вычисления.
Что значит приведенная матрица?

Приведенная матрица может быть использована для упрощения и решения линейных уравнений и систем уравнений. Применение приведенных матриц позволяет сократить и упростить операции с матрицами и векторами, что значительно упрощает вычисления и улучшает понимание решения задач линейной алгебры.
Приведенные матрицы также используются при решении задач на диагонализацию матрицы и нахождение собственных значений и собственных векторов матрицы. Они помогают выделить основные свойства матрицы и обнаружить информацию о ее собственных значениях и векторах.
Для представления приведенной матрицы обычно используется таблица, где элементы матрицы располагаются в строках и столбцах. Таблица состоит из ячеек, где каждая ячейка содержит один элемент матрицы. Использование таблицы позволяет четко и структурированно представить матрицу и ее элементы.
| а₁₁ | а₁₂ | а₁₃ |
| а₂₁ | а₂₂ | а₂₃ |
| а₃₁ | а₃₂ | а₃₃ |
Приведенная матрица может быть любого размера - от двухмерных матриц до матриц больших размерностей. Таблица позволяет удобно представить большое количество элементов и структурировать информацию, что упрощает работу с матрицами и позволяет увидеть основные свойства матрицы.
Определение и применение
Одно из главных применений приведенной матрицы заключается в решении систем линейных уравнений. Они могут использоваться для описания различных физических, экономических и инженерных проблем. Приведенные матрицы также могут быть использованы для вычисления определителя и обратной матрицы.
Приведенная матрица является важным инструментом в линейной алгебре, который позволяет решать широкий спектр задач. Знание и понимание приведенных матриц позволяет математикам, физикам, экономистам и инженерам анализировать и решать различные проблемы, используя методы линейной алгебры.
Приведение матрицы к ступенчатому виду
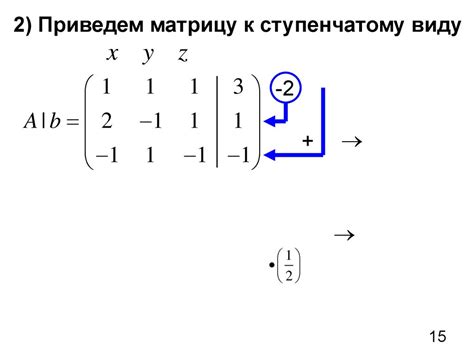
Для приведения матрицы к ступенчатому виду можно использовать элементарные преобразования строк. Элементарные преобразования включают в себя:
- Перестановку строк – меняет местами две строки матрицы.
- Умножение строки на ненулевое число – все элементы строки умножаются на одно и то же число, отличное от нуля.
- Сложение строки с другой строкой, умноженной на число – к элементам одной строки прибавляются соответствующие элементы умноженной на число строки.
Данные преобразования позволяют изменить матрицу таким образом, чтобы при переходе к ступенчатому виду появились нулевые элементы ниже главной диагонали.
Процесс приведения матрицы к ступенчатому виду заключается в следующих шагах:
- Выбирается первый ненулевой столбец матрицы и находится в нем первый ненулевой элемент. Если такого элемента нет, то процесс приведения завершен.
- Если найденный элемент не находится в первой строке матрицы, то выполняется перестановка этой строки с первой строкой.
- Выполняется элементарное преобразование строк, чтобы обнулить все элементы столбца ниже найденного элемента.
- Процесс приведения повторяется для интересующего нас отсека матрицы, начиная со следующего столбца и следующей строки.
- Повторяем шаги 1-4 до тех пор, пока не будет приведена вся матрица к ступенчатому виду.
Как только матрица будет приведена к ступенчатому виду, ее можно использовать для решения систем линейных уравнений или применять другие методы анализа и обработки матриц.
Приведение матрицы к каноническому виду
Приведение матрицы к каноническому виду происходит при помощи элементарных преобразований строк и столбцов. Элементарные преобразования позволяют изменять матрицу без изменения ее ранга и свойств. В результате приведения матрицы она принимает специальный вид, где на главной диагонали стоят только ненулевые элементы, а все остальные элементы равны нулю.
Процесс приведения матрицы к каноническому виду включает в себя следующие шаги:
- Выбор главного элемента – ненулевого элемента, стоящего в верхнем левом углу матрицы.
- Приведение главного элемента к единице путем деления всей строки на значение этого элемента.
- Приведение всех остальных элементов строки, в которой находится главный элемент, к нулю путем вычитания из каждого элемента строки произведения значения элемента этой строки на элемент столбца, в котором находится главный элемент.
- Выбор следующего главного элемента и повторение пунктов 2 и 3 для остальных строк и столбцов.
- После завершения процесса приведения все ненулевые элементы матрицы будут находиться на главной диагонали.
Приведение матрицы к каноническому виду является неотъемлемой частью решения систем линейных уравнений методом Гаусса. Полученный канонический вид матрицы позволяет легко вычислить ранг матрицы и определитель, а также найти решение системы линейных уравнений с помощью метода обратной матрицы или метода Гаусса-Жордана.
Расширенная матрица и элементарные преобразования

Расширенная матрица используется для решения систем линейных алгебраических уравнений с помощью элементарных преобразований. Элементарные преобразования позволяют сделать систему уравнений проще и найти ее решение. К элементарным преобразованиям относятся:
- Умножение строки матрицы на ненулевое число.
- Прибавление к одной строке матрицы другой строки, умноженной на некоторое число.
- Перестановка строк матрицы.
Используя элементарные преобразования, можно привести расширенную матрицу к ступенчатому виду, а затем к улучшенному ступенчатому виду или к каноническому виду. В улучшенном ступенчатом виде или каноническом виде решение системы линейных уравнений считается более удобным.
Расширенная матрица и элементарные преобразования очень полезны в линейной алгебре, так как позволяют решать сложные системы уравнений и находить решения с помощью простых операций.
Определение ранга матрицы
Ранг матрицы можно определить следующим образом:
- Преобразуйте данную матрицу к ступенчатому виду (приведенной форме). Это можно сделать, выполняя элементарные преобразования строк (умножение строки на число, прибавление строки к другой строке) и столбцов (умножение столбца на число, прибавление столбца к другому столбцу).
- Ранг матрицы равен количеству ненулевых строк в приведенной матрице.
Ранг матрицы имеет много практических применений в линейной алгебре. Например, ранг матрицы может быть использован для определения размерности линейного пространства, заданного этой матрицей, или для проверки линейной независимости системы векторов, представленных в виде этой матрицы. Более того, ранг матрицы важен при решении систем линейных уравнений и при определении обратной матрицы.
Использование приведенной матрицы в линейной алгебре

Приведенная матрица представляет собой матрицу, которая находится в наиболее удобном и понятном виде для выполнения различных операций в линейной алгебре. Она используется для упрощения вычислений и решения систем линейных уравнений.
Каждая матрица может быть приведена к определенному виду с использованием элементарных преобразований строк и столбцов. Приведенная матрица характеризуется следующими свойствами:
- Лидирующие элементы: в каждом ненулевом столбце самый верхний элемент называется лидирующим. Лидирующие элементы отличаются от нулевых и находятся слева от нулей.
- Ведущие одиницы: если в столбце с лидирующим элементом есть нули, то ведущая единица находится в той же строке, что и лидирующий элемент.
- Нижние нули: строки, расположенные ниже строки с лидирующими элементами, состоят только из нулей.
- Хвостовые строки и столбцы: строки и столбцы, расположенные правее и ниже лидирующих элементов, также состоят из нулей.
Приведенная матрица позволяет упростить операции над матрицами, такие как сложение, умножение и нахождение обратной матрицы. Она пригодна для решения систем линейных уравнений с использованием метода Гаусса или метода Гаусса-Жордана.
Используя приведенную матрицу, можно быстро и эффективно решать линейные задачи в различных областях, таких как физика, экономика, компьютерная графика и другие. Благодаря своей структуре, приведенная матрица позволяет выполнить множество операций, сократив время и упростив процесс расчетов.
Таким образом, приведенная матрица является важным инструментом в линейной алгебре, который значительно облегчает выполнение различных операций и решение задач, связанных с линейными уравнениями и матрицами.
| 1 | 0 | 2 | 0 |
|---|---|---|---|
| 0 | 1 | 3 | 0 |
| 0 | 0 | 0 | 1 |
Примеры и задачи
Вот несколько примеров и задач, где можно использовать приведенную матрицу в линейной алгебре:
- Нахождение определителя матрицы: приведенная матрица может быть использована для легкого вычисления определителя. Просто перемножьте элементы главной диагонали и получите определитель матрицы.
- Нахождение обратной матрицы: если приведенная матрица не содержит нулевых элементов и ее определитель не равен нулю, то можно использовать приведенную матрицу для нахождения обратной матрицы. Просто примените формулу обратной матрицы к элементам приведенной матрицы.
- Решение систем линейных уравнений: приведенная матрица может быть использована для решения систем линейных уравнений. Примените метод Гаусса, чтобы привести матрицу к ступенчатому виду, затем выразите неизвестные переменные через свободные.
- Разложение матрицы: приведенная матрица может быть использована для разложения матрицы на факторы, такие как LU-разложение, QR-разложение и др. Это может быть полезно для решения сложных задач, связанных с матрицами.
- Линейные преобразования: приведенная матрица может быть использована для нахождения образа и ядра линейного преобразования. Примените матрицу к векторам и проанализируйте результаты.








