Геометрия является одной из основных математических дисциплин, которая изучает пространственные формы и их свойства. Одним из важных понятий в геометрии является подобие треугольников. Подобные треугольники – это треугольники, которые имеют соответственно равные углы и пропорциональные стороны, но могут быть разных размеров и форм.
Понимание подобных треугольников является важным знанием в геометрии, так как они используются в различных областях жизни, включая архитектуру, строительство, картографию и фотографию. Например, архитекторы могут использовать подобные треугольники для создания пропорциональных и симметричных структур, а фотографы - для создания эффектов глубины и перспективы на фотографиях.
Важно отметить, что подобие треугольников основывается на соотношении их сторон и углов, что позволяет нам делать выводы о пропорциональности размеров предметов или объектов в реальном мире. Именно поэтому знание о подобных треугольниках столь значимо при решении задач в геометрии и повседневной жизни.
Важность подобных треугольников в геометрии
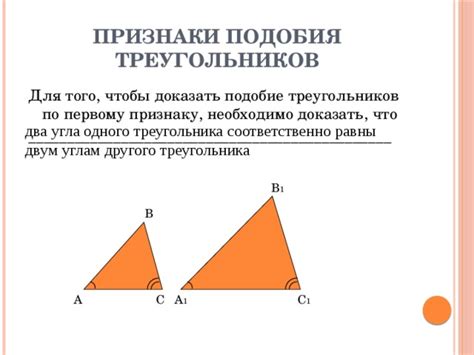
Основное свойство подобных треугольников заключается в том, что их стороны пропорциональны. Это значит, что все стороны одного треугольника имеют отношение к соответствующим сторонам другого треугольника. Такое свойство позволяет делать различные выводы и использовать их для решения задач и конструкций.
Одно из практических применений подобных треугольников - вычисление недостающих сторон и углов. Если мы знаем отношение сторон подобных треугольников, то можно вычислить недостающие стороны или углы с помощью пропорции. Например, зная отношение сторон треугольника АВС к треугольнику АВС', можно найти все недостающие стороны и углы обоих треугольников.
Подобные треугольники также используются для решения сложных задач в геометрии. Например, они могут быть использованы для вычисления высоты высокого объекта, такого как здание или дерево, без необходимости измерять его непосредственно. Достаточно измерить длину тени объекта и длину тени подобного треугольника, а затем, используя пропорции, вычислить высоту объекта.
Подобные треугольники также используются в архитектуре и инженерии при проектировании и строительстве. Они позволяют определить пропорции и размеры объектов, используемых при строительстве зданий, мостов, дорог и других инженерных сооружений.
В заключение, подобные треугольники являются важной концепцией в геометрии. Их свойства позволяют делать выводы, решать задачи и применять в практических ситуациях, что делает их неотъемлемой частью геометрии.
Геометрическая концепция искажения
Искажение в геометрии означает изменение формы или размера фигуры без изменения ее других характеристик, таких как площадь или углы. Обычно искажение связано с использованием преобразований, которые изменяют фигуру.
Одним из примеров искажения является треугольник Паскаля. Это особый тип треугольника, который получается путем соединения вершин двух смежных треугольников, таких как треугольник Серпинского. В результате такого искажения получается фрактальная структура, которая имеет бесконечное число углов и прямолинейных отрезков.
Треугольник Паскаля имеет множество интересных свойств и применений. Он используется в математике, физике, информатике и других областях. Этот треугольник помогает рассматривать различные проблемы и задачи с геометрической точки зрения и найти элегантные решения.
Таким образом, геометрическая концепция искажения помогает нам понять, как изменения формы и размера фигуры могут влиять на ее свойства и использование. Использование искаженных объектов и фигур помогает нам найти новые решения и подходы к задачам и проблемам. Геометрия искажения является важной областью исследования и применения в науке и технологии.
Практическое применение подобных треугольников

Подобные треугольники имеют множество практических применений в различных областях, таких как архитектура, инженерное дело, физика и геодезия.
Одним из примеров применения подобных треугольников является определение высоты недоступного или опасного объекта. Например, если мы хотим измерить высоту дерева или здания, но не можем подойти к нему, мы можем использовать подобные треугольники. Определенная угловая высота измеряется с помощью теодолита или другого инструмента, а затем, используя триангуляцию и подобные треугольники, можно рассчитать высоту объекта.
Другими примерами применения подобных треугольников являются определение расстояний до недоступных объектов или масштабирование карт и планов. Например, в геодезии при определении расстояний до отдаленных объектов, таких как возвышенности или горы, используется принцип подобных треугольников. С помощью треугольника, образованного из знакомого объекта и двух точек с известными угловыми размерами, можно рассчитать расстояние до недоступного объекта.
Применение подобных треугольников также находит свое применение в архитектуре и инженерном деле. Например, в строительстве зданий или мостов подобные треугольники помогают определить устойчивость и прочность конструкций.
Таким образом, подобные треугольники являются важным инструментом для решения различных задач в различных областях и применяются для измерения и рассчета различных параметров объектов.
Использование подобия при определении высоты объектов
Для этого нам необходимо иметь информацию о длинах двух сторон подобных треугольников и длине соответствующего отрезка на другом треугольнике. Например, если у нас есть треугольник АВС и треугольник ХУZ, которые подобны, и мы знаем длины сторон AB и АХ, а также длину отрезка СZ, то мы можем использовать подобие треугольников для определения длины высоты HZ. Зная соотношение длин сторон треугольников АВС и ХУZ, мы можем установить пропорцию и вычислить длину HZ.
Использование подобия треугольников при определении высоты объектов особенно удобно, когда объект находится на недоступной высоте или не может быть измерен непосредственно. Подобие треугольников позволяет нам применять геометрические принципы для решения сложных задач, связанных с измерением и определением размеров объектов.
Понимание подобия треугольников в математике
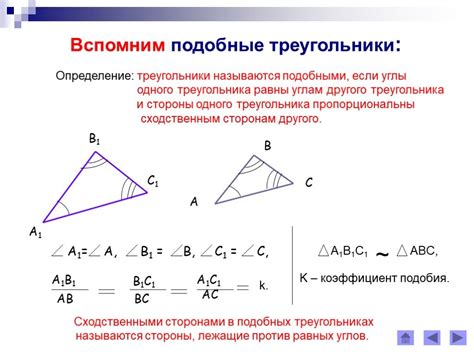
В геометрии треугольник считается подобным другому треугольнику, если соответствующие их стороны пропорциональны, а соответствующие углы равны или имеют одинаковые величины. Рассмотрим основные концепции и принципы, связанные с пониманием подобия треугольников.
- Пропорциональность сторон: Для того чтобы треугольники были подобными, соответствующие стороны должны быть пропорциональны. Это означает, что отношение длин сторон одного треугольника к длинам соответствующих сторон другого треугольника должно быть постоянным.
- Угловая подобность: Подобие треугольников также предполагает равенство или одинаковую величину их углов. Если углы одного треугольника равны соответствующим углам другого треугольника, то данные треугольники считаются подобными.
- Соотношение длин сторон и соответствующих углов: При подобии треугольников соотношение длин соответствующих сторон может быть использовано для определения соотношения значений соответствующих углов. Например, если сторона одного треугольника в два раза длиннее соответствующей стороны другого треугольника, то соответствующий угол в первом треугольнике также будет дважды больше, чем соответствующий угол во втором треугольнике.
Подобные треугольники обладают множеством интересных свойств, которые играют важную роль в различных областях математики и ее приложениях. Например, знание подобия треугольников позволяет проводить определенные вычисления, такие как нахождение длин отсутствующих сторон или углов в подобных треугольниках. Также подобие треугольников является основой для понимания и решения более сложных геометрических проблем.
Основываясь на этих концепциях подобия треугольников, математики разработали набор правил и теорем, которые позволяют определить и применять подобие треугольников в различных геометрических задачах. Понимание этих правил и принципов важно для углубленного изучения геометрии и ее применений в реальном мире.
Решение задач на пропорциональные отношения в треугольниках
Пропорциональные отношения играют важную роль в геометрии и особенно в решении задач, связанных с треугольниками. Зная некоторые пропорциональные отношения в треугольнике, можно найти значения других сторон или углов без необходимости проводить дополнительные измерения.
Для решения задач на пропорциональные отношения в треугольниках нужно использовать различные геометрические свойства и теоремы. Вот некоторые из них:
Теорема Пифагора:
Если в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов, то это соотношение можно использовать для решения задач на пропорциональные отношения.
Например, если известны длины двух сторон, а требуется найти длину третьей стороны, можно воспользоваться теоремой Пифагора для нахождения пропорционального отношения.
Теорема синусов и косинусов:
Если известны длины двух сторон и угол между ними, или длины трех сторон, то с помощью теорем синусов и косинусов можно выразить пропорциональные отношения и решить задачу.
Например, если известны длины двух сторон и угол между ними, можно воспользоваться теоремой синусов для нахождения пропорционального отношения и длины третьей стороны.
Помимо этих теорем, можно использовать и другие геометрические свойства, такие как равенство геометрических фигур или равенство сегментов. Все они помогают находить пропорциональные отношения в треугольниках и решать разнообразные задачи, связанные с этой темой.
Знание и умение использовать пропорциональные отношения в треугольниках позволяет не только решать задачи, но и лучше понимать геометрию и ее применение в реальной жизни. Это является важной частью геометрического образования и позволяет развить логическое мышление и умение анализировать сложные геометрические конструкции.








