Монотонность функции – одно из важнейших свойств, позволяющее понять, как меняется функция на определенном интервале. Знание промежутков монотонности позволяет анализировать график функции, находить экстремумы и изучать ее поведение в целом.
Определить промежутки монотонности функции можно, применив несколько методов и правил. В этом руководстве мы рассмотрим самые распространенные из них и представим подробные шаги для каждого метода.
В первую очередь, необходимо разобраться в понятии монотонности. Функция является возрастающей на интервале, если значения функции увеличиваются с ростом аргумента. Функция является убывающей на интервале, если значения функции уменьшаются с ростом аргумента. Монотонность может меняться на точках экстремума – местах, где функция достигает своих максимальных или минимальных значений.
При поиске промежутков монотонности необходимо также учитывать точки разрыва функции – точки, в которых значение функции становится неопределенным или разрывным.
Определение промежутка монотонности
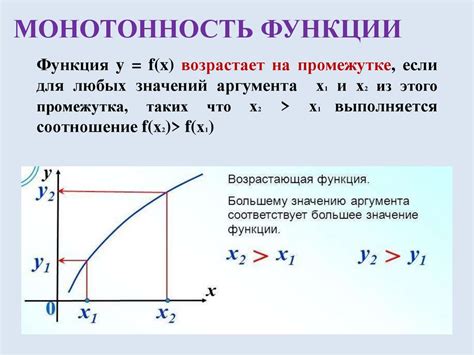
Для определения промежутка монотонности функции необходимо исследовать ее производную. Если производная положительна на некотором интервале, то функция возрастает на данном интервале. Если производная отрицательна на некотором интервале, то функция убывает на данном интервале. Если производная равна нулю на некотором интервале, то на этом интервале функция может иметь экстремумы (максимумы или минимумы).
Для определения промежутка монотонности функции необходимо выполнить следующие шаги:
- Найти область определения функции.
- Вычислить производную функции.
- Найти значения переменной, при которых производная равна нулю или не существует. Эти точки разделяют область определения на подынтервалы.
- Выбрать тестовую точку из каждого подынтервала и определить знак производной на этом подынтервале.
- Используя знаки производной и значения переменной, определить, возрастает функция, убывает функция или изменяет свою монотонность на каждом подынтервале.
Определение промежутка монотонности функции позволяет более подробно изучить ее свойства и взаимосвязи с другими функциями. Это важный инструмент в математическом анализе и позволяет более точно понять поведение функции на заданном интервале.
Как найти точки экстремума функции
Для того чтобы найти точки экстремума функции, следует выполнить следующие шаги:
- Найти производную функции.
- Решить уравнение f'(x)=0 для нахождения критических точек (точек, где производная равна нулю).
- Проверить каждую критическую точку, используя вторую производную тест или исследование знаков производных.
- Определить тип каждой критической точки (максимум или минимум).
Если вторая производная положительна в критической точке, то функция имеет локальный минимум в этой точке. Если вторая производная отрицательна, то функция имеет локальный максимум.
Если вторая производная равна нулю или не существует, следует провести исследование знаков производной. Если производная меняет знак с "плюса" на "минус" при переходе через критическую точку, то функция имеет локальный максимум. Если производная меняет знак с "минуса" на "плюс", то функция имеет локальный минимум.
Полученные точки экстремума позволяют определить поведение функции и сделать выводы о способе графического представления функции. Точки максимума и минимума являются важными особенностями функции и позволяют оценивать ее значения в различных интервалах.
Понятие возрастания и убывания функции
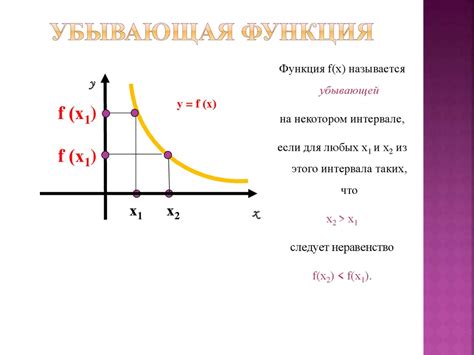
В теории функций, понятие возрастания и убывания функции играет важную роль при анализе ее свойств и поведения на промежутках.
Возрастание функции - это такой промежуток, на котором значения функции строго увеличиваются при увеличении аргумента. График функции, определенной на таком промежутке, будет иметь форму растущей кривой.
Следует отметить, что возрастание функции может быть как строгим, так и нестрогим. В случае строгого возрастания значения функции строго монотонно возрастают, а в случае нестрогого возрастания значения могут увеличиваться нестрого (включая сохранение равенства).
Убывание функции - это такой промежуток, на котором значения функции строго уменьшаются при увеличении аргумента. График функции, определенной на таком промежутке, будет иметь форму убывающей кривой.
Аналогично возрастанию, убывание функции может быть строгим или нестрогим. В случае строгого убывания значения функции строго монотонно убывают, а в случае нестрогого убывания значения могут уменьшаться нестрого (включая сохранение равенства).
Понятие возрастания и убывания функции позволяет нам анализировать ее свойства и расположение на числовой оси. Знание этих понятий поможет нам выявлять промежутки, на которых функция изменяется монотонно, а также области, где функция может иметь экстремумы.
Как найти интервалы возрастания и убывания функции
1. Найдите производную функции f'(x). Для этого возьмите производную функции f(x) по переменной x. Для нахождения производной обычно используют правила дифференцирования, такие как правило производной суммы, правило производной произведения и правило производной сложной функции.
2. Решите уравнение f'(x) = 0. Найденные значения переменной x являются критическими точками функции. На этих точках производная функции меняет знак.
3. Постройте таблицу знаков производной функции f'(x), используя найденные критические точки. Возьмите произвольную точку между критическими точками и определите знак производной функции в этой точке. Запишите знаки производной функции для каждого интервала между критическими точками.
4. Интервалы, где производная функции положительна, соответствуют интервалам возрастания функции. Интервалы, где производная функции отрицательна, соответствуют интервалам убывания функции.
5. Представьте результаты анализа в виде набора интервалов возрастания и убывания функции. Например, интервал возрастания функции может быть представлен как [a, b], где a и b - значения переменной x, а интервал убывания - как [c, d], где c и d - другие значения переменной x.
Экстремальные значения функции и их связь с монотонностью
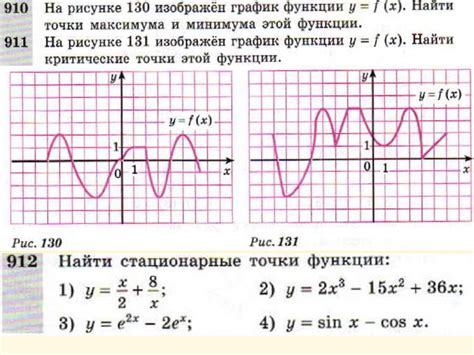
Если функция на заданном промежутке имеет максимум или минимум, то она немонотонна на этом промежутке. Если функция имеет локальный экстремум, то в окрестности этой точки она также немонотонна. Однако, на промежутке между двумя соседними экстремумами функция может быть монотонной.
Чтобы найти экстремальные значения функции, необходимо проанализировать ее производную. Если производная функции меняет знак с плюса на минус, то функция имеет локальный максимум. Если с минуса на плюс, то функция имеет локальный минимум. При этом, если производная функции равна нулю, то это может быть точкой экстремума или точкой перегиба.
Исследование экстремальных значений функции и их связь с монотонностью позволяют более полно понять ее поведение на заданном промежутке и определить промежутки, на которых она монотонна.
Как определить промежутки монотонности по графику функции
Для определения промежутков монотонности функции по ее графику необходимо анализировать изменение наклона этого графика. Хорошая визуализация и умение анализировать графики функций помогут в этом процессе.
Определение промежутков монотонности функции происходит следующим образом:
- Анализируйте график функции от начала до конца. Определите, как изменяется наклон графика. Наклон графика может быть положительным (график идет вверх), отрицательным (график идет вниз) или равным нулю (график горизонтален).
- В местах, где наклон графика изменяется, возможно изменение монотонности функции, например, с убывания на возрастание или наоборот. Обратите внимание на такие точки.
- Используйте табличный метод для более точного определения промежутков монотонности функции. В таблице запишите значения аргументов (x) и соответствующие им значения функции (f(x)).
- Анализируйте изменение значений функции от строки к строке. Если значения функции возрастают или убывают постоянно, то в этом промежутке функция монотонна. Если значения функции периодически убывают и возрастают, то функция немонотонна.
- Запишите промежутки монотонности функции, указав интервалы, на которых она возрастает или убывает.
Например, если у вас есть график функции, который сначала идет вниз (отрицательный наклон), а затем вверх (положительный наклон), функция монотонно возрастает на первом промежутке и монотонно убывает на втором. Если на промежутке наклон графика равен нулю, это может означать, что функция имеет точку экстремума.
| Аргумент (x) | Функция (f(x)) | Монотонность |
|---|---|---|
| -2 | -5 | Н/Д |
| -1 | -3 | Н/Д |
| 0 | 1 | Возрастает |
| 1 | 4 | Возрастает |
| 2 | 2 | Убывает |
| 3 | 1 | Убывает |
В данном примере функция монотонно возрастает на интервале [0, 1] и монотонно убывает на интервале [2, 3].
Важно помнить, что промежутки монотонности функции определяются исключительно по ее графику и изменению наклона. Для более точной и уверенной оценки рекомендуется также рассмотреть производную функции.
Метод первой производной для определения промежутков монотонности

Для начала, необходимо вычислить производную функции. Затем, анализируя знаки производной на различных интервалах, можно определить промежутки, на которых функция возрастает или убывает.
Если производная положительна на некотором интервале, то это означает, что функция возрастает на этом промежутке. Если производная отрицательна, то функция убывает. Если производная равна нулю, то это может указывать на точку экстремума.
Для нахождения промежутков монотонности с использованием метода первой производной следует выполнить следующие шаги:
- Вычислить производную функции.
- Найти значения x, при которых производная равна нулю или не существует (точки, в которых возможны экстремумы).
- Используя эти значения x, построить интервалы на числовой оси.
- Выбрать по одной точке из каждого интервала и проверить знак производной в этих точках.
- Сделать выводы о промежутках монотонности функции.
Применение метода первой производной требует некоторых навыков в анализе функций и их производных. Однако, освоив этот метод, можно достаточно точно определить промежутки монотонности функции и использовать это в решении задач по оптимизации и определению глобальных экстремумов.
Алгоритм определения промежутков монотонности
Для определения промежутков монотонности функции существует определенный алгоритм, который поможет нам систематически решать данную задачу. Вот шаги этого алгоритма:
1. Найдите производную функции.
Производная функции позволяет нам найти ее скорость изменения. Для этого возьмите функцию и найдите ее производную с помощью соответствующей математической формулы или правила дифференцирования.
2. Найдите точки, в которых производная равна нулю или неопределена.
Точки, где производная равна нулю или не существует (неопределена), могут быть точками экстремума или разрыва функции. Это могут быть точки перегиба или точки, где функция меняет свой рост или спад.
3. Постройте интервалы между найденными точками.
Используя найденные точки из предыдущего шага, постройте интервалы между ними. Для каждого интервала определите знак производной в этом интервале с помощью знаковой функции.
4. Определите монотонность функции на каждом интервале.
Зная знак производной в каждом интервале, определите монотонность функции на этом интервале. Если производная положительна, то функция монотонно возрастает; если производная отрицательна, то функция монотонно убывает. В противном случае функция может быть немонотонной или иметь различные монотонные участки.
Эти шаги алгоритма помогут вам систематически определить промежутки монотонности функции. Комбинирование и анализ монотонности функции позволяют нам лучше понять ее поведение и свойства.
Примеры решения задач на нахождение промежутков монотонности

Рассмотрим некоторые примеры задач, в которых требуется найти промежутки монотонности функции. Для наглядности будем использовать графики функций.
Пример 1:
Найти все промежутки возрастания и убывания функции f(x) = x^2 - 5x + 6.
Решение:
Для начала мы должны найти производную функции f(x). Производная позволяет определить, где функция возрастает или убывает.
Производная функции f(x) равна f'(x) = 2x - 5.
Чтобы найти корни производной, решим уравнение 2x - 5 = 0:
2x = 5
x = 5/2 = 2.5
Таким образом, мы получили точку разрыва в функции f(x), которая делит ее на два промежутка: (-∞, 2.5) и (2.5, ∞).
Теперь мы должны проанализировать каждый из этих промежутков, чтобы определить, возрастает или убывает функция на каждом из них.
На промежутке (-∞, 2.5) производная функции f(x) (2x - 5) всегда отрицательна (возьмем произвольное значение x на этом промежутке, например, x = 0: 2*0 - 5 = -5), следовательно, функция f(x) убывает на этом промежутке.
На промежутке (2.5, ∞) производная функции f(x) положительна (возьмем произвольное значение x на этом промежутке, например, x = 5: 2*5 - 5 = 5), что означает, что функция f(x) возрастает на этом промежутке.
Таким образом, промежутки монотонности для функции f(x) состоят из интервала (-∞, 2.5) (убывание) и интервала (2.5, ∞) (возрастание).
Пример 2:
Найти все промежутки возрастания и убывания функции g(x) = 3x^3 - 9x^2 + 12x - 4.
Решение:
Снова начнем с нахождения производной функции g(x). Производная функции равна g'(x) = 9x^2 - 18x + 12.
Чтобы найти корни производной, решим уравнение 9x^2 - 18x + 12 = 0:
3x^2 - 6x + 4 = 0
Это квадратное уравнение, решая которое, мы получаем два корня: x = 1 и x = 2/3.
Таким образом, получаем две точки разрыва в функции g(x), которые делят ее на три промежутка: (-∞, 2/3), (2/3, 1), (1, ∞).
Анализируя каждый из этих промежутков, мы можем сделать следующие выводы о значении производной и монотонности функции g(x):
На промежутке (-∞, 2/3) производная функции g(x) (9x^2 - 18x + 12) положительна (возьмем произвольное значение x на этом промежутке, например, x = -1: 9*(-1)^2 - 18*(-1) + 12 = 27), что означает, что функция g(x) возрастает на этом промежутке.
На промежутке (2/3, 1) производная функции g(x) отрицательна (возьмем произвольное значение x на этом промежутке, например, x = 0.8: 9*(0.8)^2 - 18*(0.8) + 12 = -0.96), следовательно, функция g(x) убывает на этом промежутке.
На промежутке (1, ∞) производная функции g(x) снова положительна (возьмем произвольное значение x на этом промежутке, например, x = 2: 9*2^2 - 18*2 + 12 = 12), что означает, что функция g(x) возрастает на этом промежутке.
Таким образом, промежутки монотонности для функции g(x) состоят из интервала (-∞, 2/3) (возрастание), интервала (2/3, 1) (убывание) и интервала (1, ∞) (возрастание).








