Понятие предела играет ключевую роль в математике, физике и других науках. Оно позволяет определить, как значения функции или последовательности изменяются при приближении к определенной точке или бесконечности. Понимание пределов является фундаментальным для решения сложных задач и понимания основных законов природы.
Основной принцип нахождения предела состоит в том, что если значения функции (или последовательности) стремятся к определенному числу, то можно говорить о существовании предела. Для того чтобы найти предел, необходимо определить, как функция или последовательность ведут себя при стремлении аргумента (или номера элемента последовательности) к определенным значениям.
Например, если функция приближается к определенному числу бесконечно близко, то можно сказать, что предел функции существует и равен этому числу.
Важным моментом при нахождении пределов является понятие бесконечности. Если функция или последовательность не имеют ограничений и стремятся к бесконечности, то можно говорить о существовании предела равного плюс или минус бесконечности. Это понятие играет значительную роль в анализе функций и решении задач на определение экстремумов функции.
Изучение пределов является сложной и интересной задачей математики. Применение пределов находит свое применение во многих научных и технических областях, где требуется анализ и прогнозирование сложных процессов. Понимание принципов нахождения пределов является фундаментом для дальнейшего развития математического мышления и решения сложных задач.
Что такое пределы в математике: основные понятия и определения
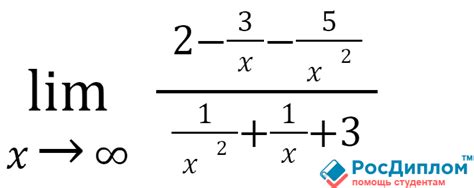
Пределы используются для анализа поведения функций или последовательностей вблизи определенных точек. Они позволяют понять, как функция ведет себя в достаточно малой окрестности данной точки.
Основные понятия и определения, связанные с пределами, включают:
- Предел функции: Предел функции f(x) при x стремящемся к a обозначается как lim f(x) = L. Это означает, что при x, близком к a, значения функции f(x) стремятся к числу L.
- Бесконечный предел: Предел функции f(x), указанный как x стремится к бесконечности, обозначается как lim f(x) = ∞ или lim f(x) = -∞. Это означает, что значения функции f(x) увеличиваются до бесконечности или уменьшаются до отрицательной бесконечности при x, стремящемся к бесконечности.
- Предел последовательности: Предел последовательности an обозначается как lim an = L. Это означает, что при n, стремящемся к бесконечности, значения элементов последовательности an стремятся к числу L.
Вычисление пределов позволяет описывать сложные функции и последовательности, а также анализировать их поведение в определенных точках или на бесконечности. Пределы являются важным инструментом в математике, используемым для решения различных задач и понимания основных концепций и законов.
Предел функции: определение, нотация и интерпретация
Определение предела функции формально записывается следующим образом:
| Определение: | Пусть функция f(x) определена на некоторой окрестности точки a (кроме, возможно, самой точки a). Говорят, что число L является пределом функции f(x), если для любого положительного числа ε существует положительное число δ такое, что для всех значений x из окрестности точки a, отличных от самой точки a, выполняется неравенство |f(x) - L| |
На практике определение предела функции можно интерпретировать следующим образом:
| Интерпретация: | Значение функции f(x) стремится к числу L, когда x приближается к точке a. |
Определение предела функции может быть записано с использованием математической нотации:
| Нотация: | L = limx→a f(x) |
В этой нотации a - это точка приближения, L - предельное значение, а lim обозначает предел функции.
Знание и понимание определения и нотации предела функции позволяют проводить анализ и изучение свойств функций, исследовать их поведение на различных интервалах и точках.
Основные типы пределов: предел функции при x стремящемся к бесконечности и предел функции при x стремящемся к какому-либо числу
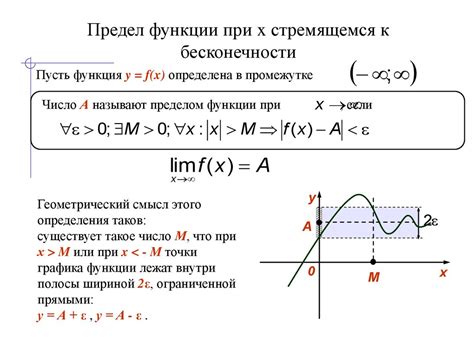
Один из основных типов пределов - это предел функции при x стремящемся к бесконечности. В данном случае, приближая значения аргумента к бесконечности, мы можем определить, к какому значению стремится значение функции. Он может быть как конечным числом, так и бесконечностью.
Другой тип предела - это предел функции при x стремящемся к какому-либо числу. В этом случае, мы фиксируем значение, к которому приближается аргумент функции, и определяем соответствующее значение функции. Здесь предел может быть как конечным числом, так и бесконечностью.
Основные принципы определения пределов включают в себя использование определения предела и соответствующих свойств функций, таких как арифметические операции, комбинирование функций, и т.д. Также важным моментом является проверка существования предела с помощью левого и правого пределов, а также анализ графика функции.
Существование предела: теоремы о существовании и условия
Для решения данной проблемы были разработаны различные теоремы, которые позволяют определить существование предела функции. Некоторые из этих теорем описаны в таблице ниже.
| Теорема | Условие | Вывод |
|---|---|---|
| Теорема о зажатой функции | Если для функций f(x), g(x) и h(x) выполняются условия: f(x) ≤ g(x) ≤ h(x) для всех x из некоторой окрестности точки a (за исключением, быть может, самой точки a), и существует предел функции f(x) и h(x) при x стремящемся к a, то и предел g(x) также существует и равен пределам f(x) и h(x). | Предел g(x) существует и равен пределам f(x) и h(x). |
| Теорема о двух милиционерах | Если для функций f(x) и g(x) выполняются условия: существуют пределы f(x) и g(x) при x стремящемся к a, и f(x) ≤ g(x) для всех x из некоторой окрестности точки a (за исключением, быть может, самой точки a), то предел f(x) не превосходит предела g(x). | Предел f(x) не превосходит предела g(x). |
| Теорема о предельном переходе в неравенствах | Если для функций f(x) и g(x) выполняются условия: существуют пределы f(x) и g(x) при x стремящемся к a, и f(x) ≤ g(x) для всех x из некоторой окрестности точки a (за исключением, быть может, самой точки a), то предел f(x) ≤ предел g(x). | Предел f(x) не больше предела g(x). |
Это лишь некоторые из теорем, которые позволяют определить существование предела функции. Различные условия могут быть применены в зависимости от задачи и характера функции. Правильное применение этих теорем поможет установить наличие предела и провести его вычисление.
Непрерывность функций: связь с понятием предела и основные свойства

Таким образом, непрерывность функции в точке a можно сформулировать следующим образом: для любого положительного числа ε существует положительное число δ такое, что если аргумент функции лежит в интервале (a-δ; a+δ), то значение функции также лежит в интервале (f(a)-ε; f(a)+ε).
Основные свойства непрерывных функций включают:
- Непрерывность функции в каждой точке своего определения;
- Непрерывность функции в точке a влечет условие существования предела функции в этой точке;
- Арифметические операции над непрерывными функциями дают непрерывные функции;
- Суперпозиция непрерывных функций также дает непрерывную функцию;
- Элементарные функции являются непрерывными на своей области определения.
Непрерывная функция является основой для многих понятий и теорем в математическом анализе, а понимание ее связи с пределами и основными свойствами позволяет эффективно анализировать и решать задачи из различных областей математики и приложений.
Значение предела: конечный, бесконечный, несуществующий или неопределенный предел
В математике предел функции определяется как значение, к которому функция стремится приближаться бесконечно близко, когда независимая переменная приближается к определенной точке.
Предел функции может быть различным: конечным, бесконечным, несуществующим или неопределенным. В зависимости от поведения функции, когда переменная стремится к определенной точке, мы можем определить значение предела.
Конечное значение предела означает, что функция сходится к определенному числу приближаясь к определенной точке. Оно может быть положительным или отрицательным.
Бесконечный предел означает, что функция стремится к бесконечности приближаясь к определенной точке. Это может быть положительная или отрицательная бесконечность, или функция может быть неограничена.
Несуществующий предел означает, что функция не имеет определенного предела приближаясь к определенной точке. Это может быть вызвано разными факторами, такими как осцилляция или разрывность функции.
Неопределенный предел означает, что предел функции имеет непонятное или неопределенное значение. Примерами неопределенных пределов являются пределы вида "бесконечность минус бесконечность" или "ноль на ноль".
Пределы имеют важное значение в математическом анализе и используются в различных областях науки и инженерии. Они помогают нам лучше понять поведение функций и решать различные задачи, связанные с аппроксимацией и предсказанием значений функции.
Арифметические свойства пределов: сумма, разность, произведение и частное
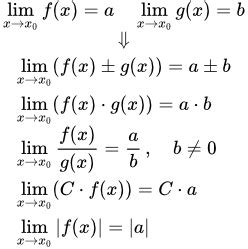
1. Сумма: Пусть f(x) и g(x) – две функции, пределы которых существуют в точке x₀. Тогда предел суммы двух функций равен сумме пределов этих функций:
Если
- limₓ→x₀ f(x) = a,
- limₓ→x₀ g(x) = b,
то
- limₓ→x₀ (f(x) + g(x)) = a + b.
2. Разность: Пусть f(x) и g(x) – две функции, пределы которых существуют в точке x₀. Тогда предел разности двух функций равен разности пределов этих функций:
Если
- limₓ→x₀ f(x) = a,
- limₓ→x₀ g(x) = b,
то
- limₓ→x₀ (f(x) - g(x)) = a - b.
3. Произведение: Пусть f(x) и g(x) – две функции, пределы которых существуют в точке x₀. Тогда предел произведения двух функций равен произведению пределов этих функций:
Если
- limₓ→x₀ f(x) = a,
- limₓ→x₀ g(x) = b,
то
- limₓ→x₀ (f(x) * g(x)) = a * b.
4. Частное: Пусть f(x) и g(x) – две функции, пределы которых существуют в точке x₀, и предел g(x) не равен нулю. Тогда предел частного двух функций равен частному пределов этих функций:
Если
- limₓ→x₀ f(x) = a,
- limₓ→x₀ g(x) = b,
- b ≠ 0,
то
- limₓ→x₀ (f(x) / g(x)) = a / b.
Арифметические свойства пределов позволяют упростить нахождение пределов сложных функций и сформулировать их в более простой форме. Эти свойства основаны на свойствах арифметических операций и позволяют нам делать выводы о пределах их комбинаций.
Теорема о пределе композиции функций: условия применимости
В математическом анализе, теорема о пределе композиции функций позволяет вычислять предел сложной функции через пределы внутренних функций. Она имеет следующую формулировку:
| Пусть | g(x) и f(y) | – функции, определенные на соответствующих подмножествах действительных чисел, |
| и |
| – пределы функций g(x) и f(y) при x, соответственно приближающемся к точке a и y, соответственно приближающемся к точке L. |
| Если | g(x) | не принимает значения L в некоторой окрестности точки a (за исключением, возможно, самой точки a), |
| тогда | limx→a f(g(x)) = M | – предел сложной функции f(g(x)) при x, приближающемся к точке a. |
Эта теорема позволяет находить предел сложной функции, используя пределы внутренних функций. Однако для применения теоремы необходимо, чтобы предел внутренней функции g(x) приближался к значению L, которое не является точкой непрерывности функции g(x).
Определение предела последовательности: связь с пределом функции и примеры

Предел последовательности {an} - это число, к которому стремятся элементы последовательности при достаточно больших значениях натурального числа n. Обозначается как lim(n→∞) an или просто lim an.
Связь между пределом последовательности и пределом функции заключается в том, что при определенных условиях предел последовательности может быть равен пределу функции. Если последовательность {an} является последовательностью значений функции f(x) при x→a, то предел последовательности совпадает с пределом функции при x→a и обозначается как lim(x→a) f(x) или просто lim f(x).
Примерами пределов последовательностей могут быть следующие:
- Последовательность {1/n}, где каждый элемент равен единице, разделенной на n. Ее предел при стремлении n к бесконечности будет равен 0.
- Последовательность {(-1)^n}, где каждый элемент чередуется между -1 и 1. У данной последовательности нет предела, так как она не стремится к какому-либо конкретному числу.
- Последовательность {sqrt(n)}, где каждый элемент равен квадратному корню из n. Ее предел при стремлении n к бесконечности будет равен бесконечности, так как квадратный корень будет увеличиваться при увеличении n.
Определение предела последовательности является важным инструментом в анализе и используется для изучения сходимости и расходимости последовательностей. Знание связи с пределом функции помогает понять свойства функций и их поведение в окрестности определенной точки.
Пределы в математическом анализе: применение в решении задач и практике
Применение пределов в решении задач и практике позволяет анализировать различные физические явления, такие как движение тела, изменение скорости или температуры и т.д. Пределы также играют важную роль в определении производных и интегралов, которые широко используются в физике, экономике, статистике и других науках и прикладных областях.
Пределы имеют ряд ключевых моментов и принципов, которые важны для правильного и эффективного решения задач. Одним из ключевых моментов является понимание понятия "приближение". Когда мы говорим о пределе функции или последовательности, мы имеем в виду, что значения функции или последовательности становятся все ближе и ближе к определенному значению по мере приближения к определенной точке. Пределы также позволяют определить, сходится ли функция или последовательность к определенному значению или расходится.
Другим важным принципом в применении пределов является использование арифметических свойств. Пределы позволяют выполнять арифметические операции с функциями и последовательностями, такие как сложение, вычитание, умножение и деление. Это особенно важно при решении сложных задач, где требуется использовать несколько функций или последовательностей, объединенных вместе.
В заключение, пределы играют важную роль в математическом анализе и имеют широкое применение в решении задач и практике. Они позволяют нам анализировать поведение функций и последовательностей в окрестности определенной точки и выполнять арифметические операции с ними. Правильное применение пределов позволяет решать сложные задачи и строить более точные математические модели, которые широко используются в науке и технике.








